3.5. Шифр Энигмы
Предшественницей современных криптографических машин была роторная машина, изобретенная в 1917 году Эдвардом Хеберном. Впоследствии она получила называние Энигма. Независимая промышленная версия была создана чуть позже берлинским инженером Артуром Кирхом. Промышленные образцы этой машины изготовляла фирма Siemens.
Энигма вначале представляла собой четыре вращающихся на одной оси барабана, что обеспечивало более миллиона вариантов шифра простой замены, которые определялись текущим положением барабанов. На каждой стороне барабана по окружности располагались 25 электрических контактов (сколько букв в алфавите). Контакты с обеих сторон барабана соединялись попарно случайным образом 25 проводами, формировавшими замену символов. Колеса складывались вместе и их контакты, касаясь друг друга, обеспечивали прохождение электрических импульсов сквозь весь пакет колес. Перед началом работы барабаны поворачивались так, чтобы устанавливалось заданное кодовое слово – ключ. При нажатии клавиши и кодировании очередного символа правый барабан поворачивался на один шаг. После того, как барабан делал полный оборот, на один шаг поворачивался следующий барабан (как в счетчике электроэнергии). Таким образом получался ключ заведомо гораздо более длинный, чем текст сообщения.
Например, в первом правом барабане провод от контакта, соответствующего букве U, присоединен к контакту буквы F на другой его стороне (рис. 3.1). Если же барабан поворачивался на одни шаг, то этот же провод соответствовал замене следующей за U буквы V на следующую за F букву G. Т.к. барабаны соприкасались контактами, то электрический импульс от нажатой клавиши с буквой исходного текста прежде чем достигал выхода претерпевал 4 замены: по одной на каждом барабане.
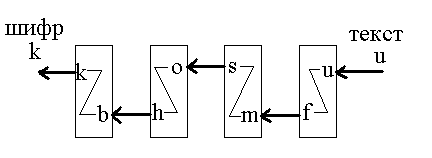
Рис. 3.1. Роторная машина Энигмы.
Дальнейшее усовершенствование этой машины сделало движение барабанов хаотичным, а их число увеличилось сначала до 5, а потом до 6. Все устройство могло поместиться в портфеле и было так просто, что обслуживалось обычными связистами.
При моделировании машины Энигмы инженера Кирха на ЭВМ можно достичь хорошей устойчивости при сравнительной простоте программы.
В чем же была слабость шифра?
1. Пять барабанов могли обеспечить около 100 миллионов ключей, что позволяло их перебрать на ЭВМ за день. Если использовать не 25 латинских символов, а 256 кодов ASCII и увеличить число барабанов, то сложность раскалывания шифра существенно возрастет.
2. Набор барабанов был ограничен и менялся редко, что вызывало охоту англичан за их экземплярами на подводных лодках. ЭВМ может для каждой шифровки использовать индивидуальные барабаны, генерируемые по ключу, что резко усложняет вскрытие шифра.
3. Можно сделать движение барабанов хаотичным, по случайной последовательности, вырабатываемой по ключу.
Подсчитаем число ключей такого шифра, реализованного программно. Пусть длина периода программного генератора случайных чисел равна 224. Восемь барабанов, генерируемые с помощью этого генератора, дадут вместе 2192 вариантов ключа. Если учесть еще варианты псевдослучайной последовательности, управляющей движением барабанов, то получится цифра в 2216 вариантов ключа.
Таким образом довольно просто получить устойчивый шифр при использовании программного генератора случайных чисел с периодом малой для криптографии длины.