2.1. Кинематическое исследование плоских рычажных механизмов графическими методами

Графические методы позволяют получить наглядные и достаточно точные решения. Ниже рассмотрены основные графические методы исследования: метод планов положений, метод кинематических диаграмм, метод планов скоростей и планов ускорений.

2.1.1. Задача о положениях звеньев

Взаимное расположение движущихся звеньев механизма все время изменяется, но в каждый данный момент времени звенья занимают вполне определенные положения. Графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени, называется планом механизма. Ряд следую­щих друг за другом планов позволяет наглядно проследить за движением звеньев и перемещением точек по траекториям.

Сборки механизма

Например, на рис. 2.1 сплошными и точечными линиями показаны две возможные сборки шарнирного четырехзвенника. Обычно при эксплуатации механизмы работают в одной из возможных сборок во всём диапазоне движений входного звена, не переходя в другую сборку.

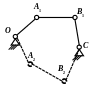
Рис. 2.1. Возможные монтажные схемы (сборки) шарнирного четырёхзвенника.

Построение планов положений

Построение плана механизма необходимо начинать с изображения по заданным координатам неподвижных элементов звеньев и направляющих. Затем изображают начальное звено в заданном положении. После этого определяют положения точек групп Ассура. В группах Ассура второго класса эти положения точек определяются методом засечек. Для определения траектории какой либо точки необходимо построить несколько последовательных планов механизма, определить положение этой точки на каждом из планов и соединить их плавной кривой.

Рассмотрим построение планов положений на примере кривошипно-ползунного механизма, кинематическая схема которого изображена на рис..2.2. Кривошип OA вращается равномерно, следовательно, в равные промежутки времени палец кривошипа A проходит одинаковые участки пути. Делим траекторию пальца А кривошипа, представляющую окружность на 12 равных частей, обозначив начальное положение, при котором кривошип и шатун располагаются по одной прямой линии, через A₀.

Рис. 2.2. План положений кривошипно-ползунного механизма

Траекторией точки B ползуна является горизонтальная прямая xx. Находим последовательные положения точки B, соответствующие положениям ведущей точки A. Длина шатуна остается неизменной в течение всего движения. Поэтому для нахождения соответствующего положения точки B_i делаем засечку на траектории x-x радиусом AB, поставив ножку циркуля в соответствующую точку A_i. Построение производим в масштабе μ_S [м/мм].

Масштабным коэффициентом (масштабом) μ_S называется отношение действительного значения физической величины к длине отрезка в мм, который изображает эту величину на чертеже. Масштабный коэффициент планов механизма определим как отношение истинной длины кривошипа l_OA к длине OA, изображающего кривошип на плане (рис. 2.1)

μ_S = l_OA / OA [м/мм].

Соединив плавной кривой точки S_i, обозначающие центры тяжести последовательных положений шатуна, получим траекторию его центра тяжести, которая относится к семейству шатунных кривых. Точно так же можно построить траекторию любой точки любого звена рычажного механизма.