1.7. Лишние степени свободы, пассивные связи и их влияние на работоспособность машин

Если результаты, полученные по структурным формулам, не соответствуют реальной степени подвижности механизма, то это может свидетельствовать о наличии в механизме лишних степеней свободы или пассивных связей.

Пример механизма с лишней степенями свободы представлен на рис. 1.13,а. На рис. 1.13,а показан сдвоенный параллелограмм, в схему ко­торого введено дополнительное звено AB = CD. (ОА = BE, AC = CD).

По формуле Чебышева имеем: .

В действительности степень подвижности механизма W =1, т.к. при заданном движении звена 1 остальные движутся вполне определенно. Дополнительное звено АВ в силу особого выбора размеров звеньев (фигуры ACDB и ОАВЕ являются параллелограммами) не налагается новых связей. Такие звенья и кинематические, которые они образуют, называют пассивными условиями связи.

На рис. 1.13,б показан механизм с пассивной связью. В этом механизме пассивной связью является звено 2.

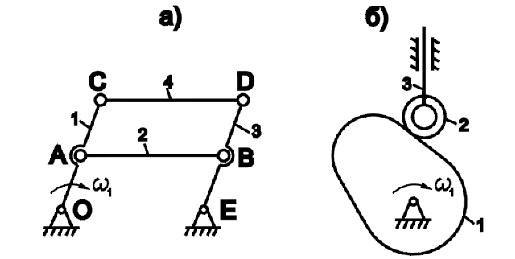
Рис. 1.13. Кинематические схемы механизмов.

а) – рычажный механизм с пассивной связью; б) – кулачковый механизм с лишней степенью свободы.

У кулачкового механизма (рис.1.13,б) по формуле Чебышева ,

хотя движение толкателя 3 полностью определяется движением кулачковой шайбы 1. Лишняя степень свободы появилась из-за возможности произвольного вращения ролика 2 вокруг своей оси. Она не влияет на кинематику толкателя. Введение в конструк­цию ролика позволяет уменьшить трение в высшей кинематической паре, а, следовательно, и ее износ.

Избыточные связи могут возникать в плоских механизмах также из-за погрешностей изготовления и монтажа звеньев, приводящих к перекосам осей кинематических пар. При этом плоский механизм фактически превращается в пространственный. Количество избыточных связей в плоских механизмах, возникающих из-за перекоса осей равно

q = W_ПЛ – W_ПР,

где W_ПЛ, W_ПР – степени подвижности механизма, рассчитанные соответственно по формулам (1.1), (1.2).

Чем больше число избыточных связей q, тем менее надежно работает механизм.

Пусть плоский механизм с четырьмя вращательными парами (n =3, р₅ = 4, W_ПЛ = 1, рис. 1.14,а) из за неточностей изготовления (например, вследствие непараллельности осей О и С) оказался пространственным. Для пространственного механизма W_ПР = 6 х n – 5х р₅ = 6х3 – 5х4 = –2. Количество избыточных связей q = 1 – (–2) = 3. Для образования механизма без избыточных связей нужна другая структурная схема, например, изображенная на рис. 1.14,б, где n =3,

р₅ = 2, р₄ = 1, р₃ = 1, W_ПР = 6 n – 5 р₄ – 4 р₅ – 3х р₃ = 6∙3 – 5∙2 – 4 – 3 = 1.

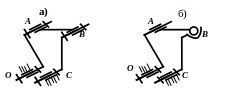
Рис. 1.14. К образованию механизма без избыточных связей.

а – механизм с избыточными связями; б – механизм без избыточных связей.

1.8.* Замена в плоских механизмах высших пар кинематическими цепями, содержащими низшие пары.

В общем случае плоский механизм состоит из звеньев, входящих в пары 4-го и 5-го классов. Многие методы решения самых разнообразных задач применимы для плоских механизмов, которые содержат звенья, входящие только в пары 5-го класса. Чтобы применить эти методы для механизмов, содержащих и пары 4-го класса необходимо пары 4-го класса на чертеже заменить кинематической цепью, в которой имеются только пары 5-го класса. Таким образом, любой плоский механизм на чертеже может быть представлен после замены как механизм, состоящий из звеньев, входящих только в пары 5-го класса. Не следует думать, что пары 4-го класса чем-то не удовлетворяют при эксплуатации машины. Они также широко распространены в машинах, как и пары 5-го класса. Например, все виды зубчатого зацепления представляют собой пары 4-го класса.

Замену можно произвести на следующих условиях:

а) число степеней подвижности механизма после замены не меняется;

б) относительное движение звеньев механизма сохраняется.

Если профили звеньев пары 4-го класса представляют собой кривые переменной кривизны (рис. 1.15 а), то в рассматриваемый момент отыскиваем центры кривизны этих кривых A и B, располагающихся на нормали N-N. Радиусами кривизны r₁ и r₂ проводим две окружности.

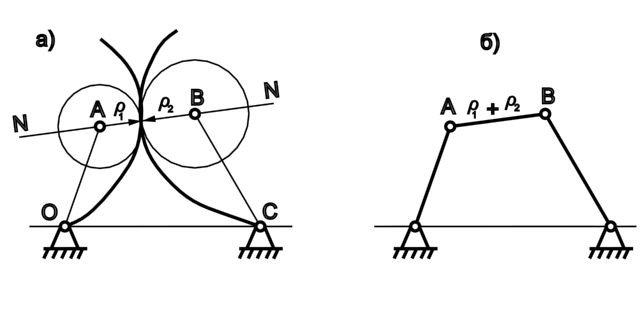
Рис. 1.15. Замена высшей пары кинематической цепью с низшими парами

В том случае, когда профилем одного из звеньев пары 4-го класса является точка (рис 1.17, а, точка В), в заменяющем механизме одна из пар, в которую входит заменяющее звено, совпадает с этой точкой (рис 1.17, б).

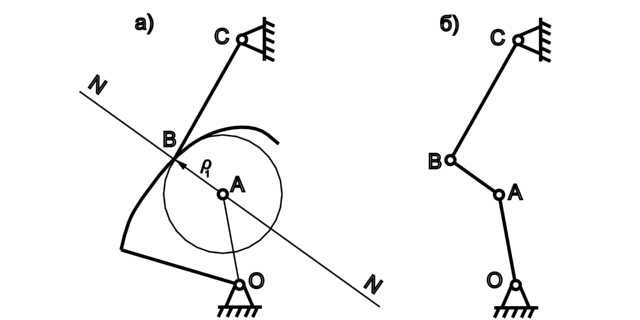
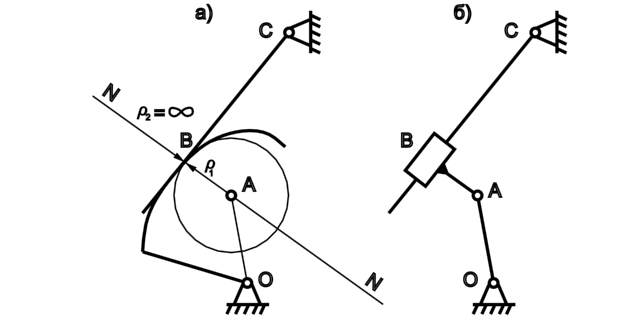
Рис. 1.16. Рис. 1.17.

Если же профиль одного из звеньев пары 4-го класса – прямая, то центр кривизны располагается в бесконечности (рис 1.16, а). Относительное вращательное движение с центром в бесконечности, можно представить как поступательное. Звено АВ, заменяющее пару 4-го класса, в этом случае входит в поступательную и вращательную пары (рис 1.16, б).