10.2. Расчетное уравновешивание неуравновешенных вращающихся масс расположенных в одной плоскости

Уравновешивание одной массы

Имеем звено, в котором на расстоянии от оси вращения l₁ располагается неуравновешенная масса m₁ (рис. 10.2). В общем случае звено может вращаться с переменной скоростью, т. е. кроме угловой скорости ω будет иметь место угло­вое ускорение ε. В результате действуют две силы инерции: центробежная Р_и1 и касательная Р^τ₁.. Каждая из этих сил будет восприниматься опорой О. Модули этих сил соответственно равны: , . Уравновесим вначале силу Р_и1 введя дополнительную массу т на расстоянии l по линии действия силы Р_и1.

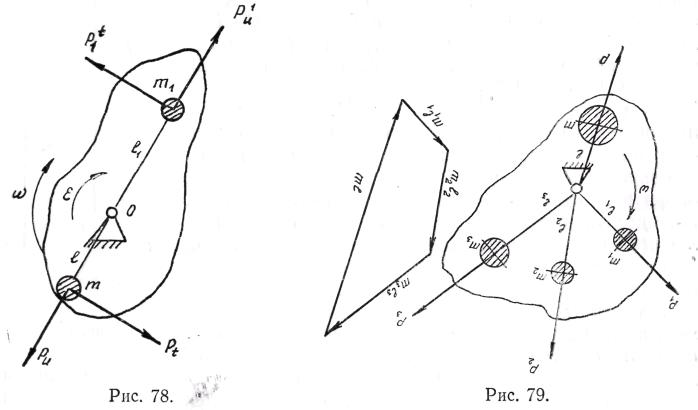
Рис. 10.2. Уравновешивание одной массы

Условие уравновешивания

Р_и1+ Р_и = 0. (10.1)

Подставив в уравнение (10.1) значение сил и сократив полученное после подста­новки уравнение на общий множитель ω², получим

m₁l₁ + ml = 0. (10.2)

Это и будет условие уравновешивания силы Р_и1.

Следовательно, для того чтобы уравновесить центробежную силу, необходимо при­ложить дополнительную массу таким образом, чтобы сумма статиче­ских моментов дополнительной массы и неуравновешенной массы относительно оси вращения равнялась нулю.

С приложением до­полнительной массы т возникает не только центробежная сила P_и, но и касательная сила, равная по модулю P^t = m ε l.

Условие (8.2) умножим на ε, тогда векторная сумма m₁εl₁ + mεl = 0 или

Р^τ₁ + Р^τ = 0. Это есть условие равновесия касательных сил.

Следовательно, условие уравновешивания центробежных сил (10.2) вместе с тем является и условием уравновешивания касательных сил, т. е. полным условием уравновешивания массы т₁. Значит, при уравновешивании масс необходимо уравновешивать центробежные силы инерции, касательные же силы инерции будут уравновешиваться автоматически. Поэтому в дальнейшем будем рассматривать только центробежные силы инерции.

Уравновешивание нескольких масс, расположенных в одной плоскости

Рассмотрим звено (рис. 10.3, слева), на котором располагаются три неуравновешенных массы т₁, m₂, m₃ соответственно на расстоянии l₁, l₂, l₃ от оси вращения О.

Задача для многих масс решается совершенно аналогично, поэтому в случае необходимости можно рассмотреть уравновешивание и большего числа масс. При вращении звена с угловой скоростью будут возникать центробежные силы инерции, равные соответственно по модулю

P₁ = ω² l₁ m₁; P₂ = ω² l₂ m₂; P₃ = ω² l₃ m₃.

Для устранения действия этих сил на опору О необходимо приложить дополнительную силу Р при условии, что Р ₁ + Р ₂ + Р ₃ + Р = 0. Полагаем, что сила Р является результатом приложения массы т к звену па расстояние l от оси вращения, тогда P= ω ² l m.

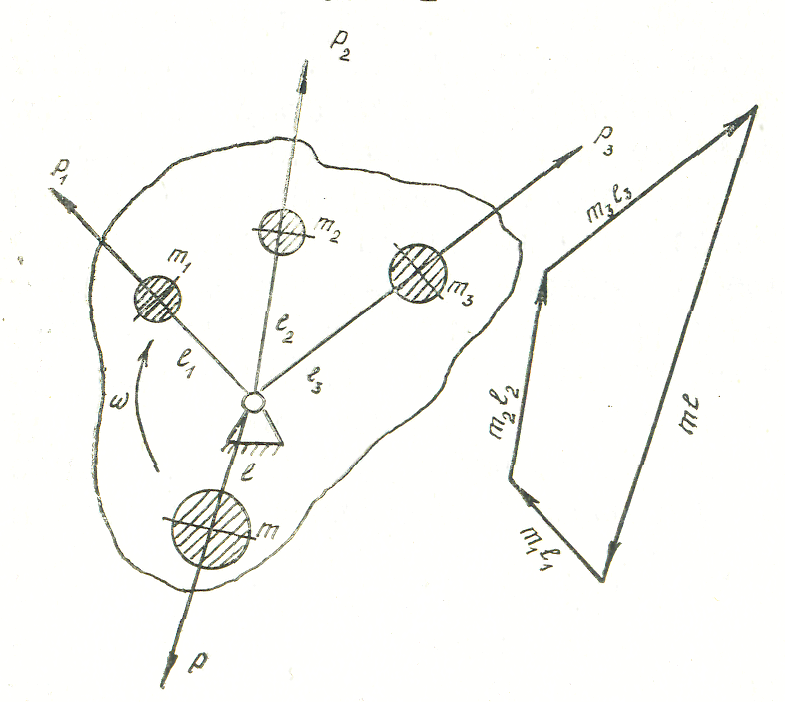
Рис. 10.3. Уравновешивание нескольких масс

Подставив в уравнение значения сил, и сократив полученное после подстановки уравнение на ω², получим условие уравновешивания масс в виде векторной суммы статических моментов

m₁ l₁ + m₂ l₂ + m₃ l₃ +m l = 0. (10.3)

Неизвестный вектор m l определяем путем построения этого уравнения . Зная вектор m l, задавшись т, находим l или, задавшись l, отыскиваем т и располагаем их на звене (см. рис. 10.3, слева). Таким образом, несколько неуравновешенных масс, располагающихся в одной плоскости, можно уравновесить одной массой, располагающейся в той же плоскости.