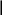1.2 Классификация кинематических пар (рис 1.2...1.3 и табл. 1.2)

Для удобства структурного анализа механизмов кинематические пары классифицируются по различным признакам:

1. По числу условий связей пары делят на 5 классов

(терминология И. И. Артоболевского), номер класса равен количеству связей, наложенных на относительное движение звеньев.

2. По виду элементов пары делят на низшие и высшие. К низшим относят кинематические пары, элементами которых являются поверхности. Элементами высших пар являются линии или точки (рис 1.3 а, б).

3. По характеру относительного движения звеньев различают поступательные и вращательные кинематические пары.

На рис. 1.2. изображены пары 1-го, 2-го, 3-го и 4-го классов. Рассмотрим их подробнее.

в)

г)

а)

б)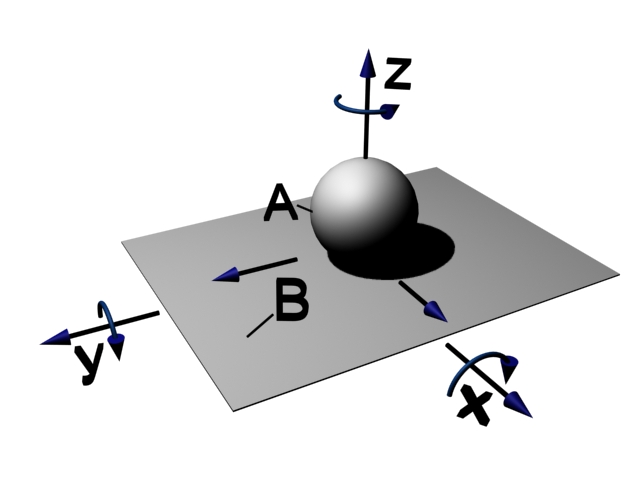

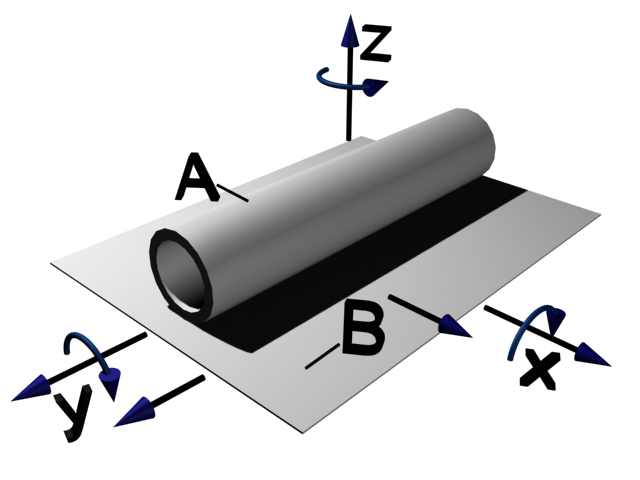
Рис 1.2. Кинематические пары 1...4 классов

Пара 1-го класса (рис. 1.2.а) – шар на плоскости. Наложено одно условие связи: исключено поступательное движение вдоль оси «Z».

Пара 2-го класса (рис. 1.2.б) – цилиндр на плоскости. Наложено два усло­вия связи: исключено поступательное движение вдоль оси «Z» и вращательное вокруг оси «X».

Пара 3-го класса (рис. 1.2.в) – шаровой цилиндр. Наложено три условия связи: исключены поступательные движения вдоль всех трёх осей.

Пара 4-го класса (рис. 1.2.г) – втулка на валике. Наложено четыре условия связи, исключе­ны поступательные и вращательные движения вдоль осей «X» и «Z».

На рис. 1.3. показаны кинематические пары 5-го класса:

1) Вращательная (рис. 1.3. а) – цилиндрический шарнир. Наложено пять условий связи: исключены все движения, кроме вращательного.

2) Поступательная (рис. 1.3. б) – наложено пять условий связи: исключены все движе­ния, кроме одного поступательного.

3) Винтовая (рис. 1.3. в) – наложено пять условии связи: исключены все движения, кроме поступательного. (Вращение не вносит степени свободы, т.к. в данном случае поступательное и вращательное движения не независимы).

Рис. 1.3. Кинематические пары 5-го класса.

1.3. Кинематическая цепь. Механизм. Степень подвижности механизма

Кинематической цепью называется связанная система звеньев, образующих между собой кинематические пары.

Кинематические цепи могут быть плоскими и пространственными. В плоских цепях все звенья перемещаются либо в одной, либо в параллельных плоскостях. Все другие цепи будут пространственными. Кинематические цепи могут быть открытыми и замкнутыми (рис. 1.4).

a	б

Рис. 1.4. Кинематические цепи (а – открытая; б–замкнутая)

Таблица 1.2

Классификация и условные обозначения кинематических пар

Число степеней подвижности W	Класс пары S	Вид пары	Условное обозначение	Низшая или высшая
1	5	Поступательная		Низшая
1	5	Вращательная		Низшая
1	5	Винтовая		Низшая
2	4	Цилиндрическая		Низшая
3	3	Сферическая (трехподвижная)		Низшая
3	3	Плоскостная		Низшая
4	2	Цилиндр – плоскость		Высшая
5	1	Шар – плоскость		Высшая

Механизмом называется кинематическая цепь с одним неподвижным звеном – стойкой, в которой при заданном законе движения одного или нескольких звеньев, все остальные звенья будут перемещаться по вполне определенным законам.

Структурная схема механизма может существенно отличаться от его реального конструктивного исполнения. Например, на рис. 1.5, 1.6 показаны общие виды щековых дробилок. На рис.1.7 – структурные схемы этих дробилок.

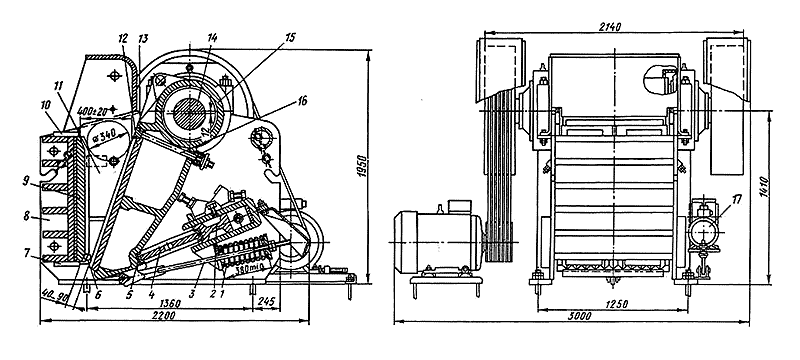
Рис.1.5 Общий вид дробилки.

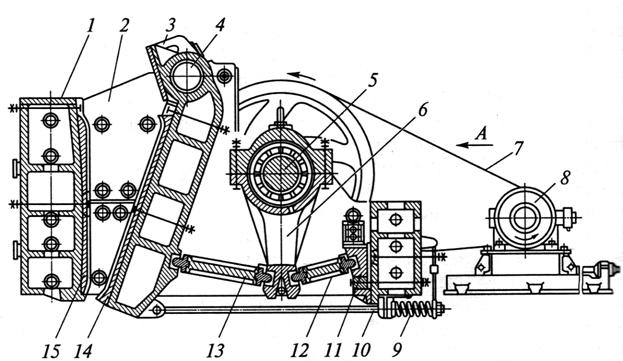
Рис.1.6. Схема щековой дробилки с простым ходом подвижной плиты

Схема для рис. 1.5.	Схема для рис. 1.6.

Рис.1.7. Структурные схемы рычажных механизмов дробилок

Обобщенная координата механизма – независимая координата, однозначно определяющая положение всех звеньев механизма относительно стойки. На механизмах, изображенных на рис. 1.7 угол поворота входного звена − кривошипа, обозначенного стрелкой, полностью определяет положение остальных звеньев, если заданы их длины. Поэтому угол поворота кривошипа является обобщенной координатой механизма.

Степенью подвижности механизма называется число степеней свободы относительно стойки, т.е. неподвижного звена. Число степеней подвижности W равно числу обобщенных координат механизма и показывает скольким звеньям

нужно задать независимые движения. При W = l механизм имеет только одно входное звено.

Для определения степени подвижности механизма в зависимости от его строения служат структурные формулы. В общем случае для пространствен­ного механизма (структурная формула Сомова – Малышева):

, (1.1)

где n – число подвижных звеньев; S – число условий связи; p₅ – число пар 5-го класса; р₄ – число пар 4-го класса; р₃ – число пар 3-го класса;

р₂ – число пар 2-го класса; p₁ – число пар 1-го класса.