5.2. Прямозубая цилиндрическая передача

Основные параметры зубчатого зацепления

Часть зуба, выступающая за начальную окружность (рис. 5.3), называется начальной головкой зуба, а часть, располагающаяся до начальной окружности, – начальной ножкой зуба.

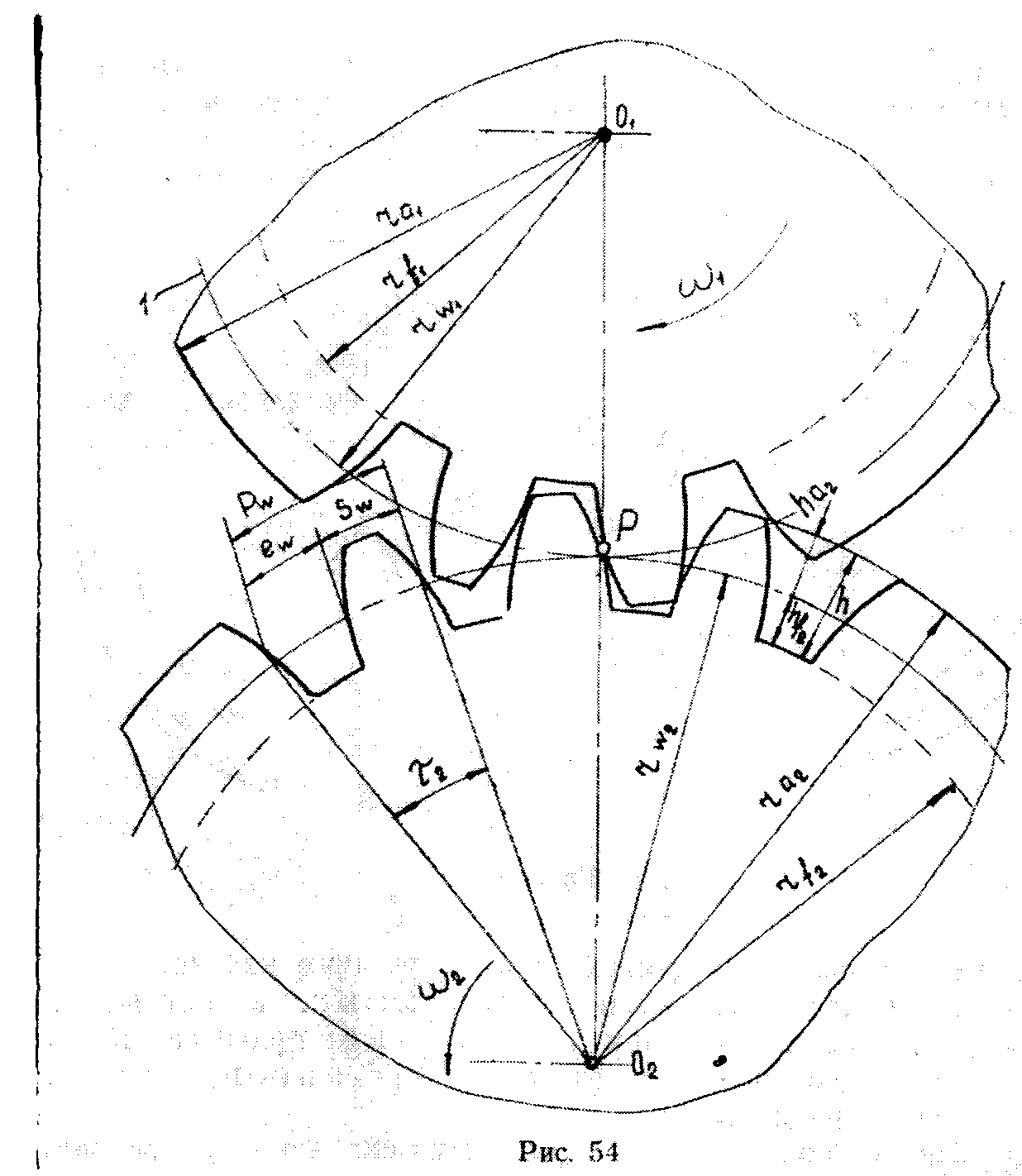
Рис. 5.3. Основные геометрические параметры зубчатого зацепления

Окружность, ограничивающая головки зубьев, называется окружностью вершин, а окружность, ограничивающая впадины зубьев, – окружностью впадин. Геометрические параметры, относящиеся к окружностям вершин, обозначаются индексом а. Геометрические параметры, относящиеся к окружностям впадин, обозначаются индексом f.

Расстояние между одноимёнными профилями соседних зубьев, измеренное по дуге окружности, называется шагом р. Шаг может быть измерен по окружности произвольного радиуса. Центральный угол зубчатого колеса, равный , называется угловым шагом зубьев. Длина дуги окружности, которую занимает зуб, это толщина зуба, длина дуги окружности, занимаемая впадиной, – ширина впадины.

Введём обозначения: r_w1 и r_w2 – радиусы начальных окружностей; h_aw и h_fw – соответственно высота начальной головки и высота начальной ножки зуба; r_a1 и r_a2 – радиусы окружностей вершин; r_f1 и r_f2 – радиусы окружностей впадин; s_w и e_w – соответственно толщина зуба и ширина впадины по начальной окружности; τ₁ и τ₂ – угловой шаг зубьев; z₁ и z₂ – числа зубьев зубчатых колёс.

Из принятых определений следует s_w + e_w = p_w . Шаг по начальным окружностям обоих зубчатых колёс одинаков. Для начальных окружностей толщина зуба колеса 1 равна ширине впадины колеса 2 при отсутствии бокового зазора в зацеплении. Для зубчатых колёс и .

Из этих равенств получим r_w2 / r_w1 = z₂ / z₁. С учётом уже известного выражения для передаточного отношения

u₁₂ = ω₁ /ω₂ = n₁ / n₂ = ± r_w2 / r_w1 = ± z₂ / z₁ .

Длина дуги произвольной окружности с радиусом равна , откуда . Обозначим символом и назовём эту величину модулем для заданного радиуса. Следовательно, у зубчатого колеса может быть бесчисленное множество модулей. Обычно все параметры зубчатых колёс и зацепления принято выражать через модуль, который соответствует ГОСТу. Такой модуль зубчатых колёс, находящихся в зацеплении, будет только один.

Окружность зубчатого колёса, пересекающая зуб, у которой модуль соответствует ГОСТу, называется делительной окружностью. Все геометрические параметры, относящиеся к делительным окружностям, индексами не обозначаются. Радиусы этих окружностей r_w2 / r_w1 = z₂ / z₁

r₁ = m z₁ / 2 и r₂ = m z₂ / 2,

где m – модуль зацепления, соответствующий ГОСТу.

Взяв отношение радиусов делительных окружностей, получим

u₁₂ = ω₁ /ω₂ = ± r_w2 / r_w1 = ± z₂ / z₁ = ± r₂ / r₁.

5.2.2. Эвольвента окружности и её свойства

Существует множество кривых профилей зубьев, обеспечивающих постоянство передаточного отношения. Однако, на практике а основном используют зацепление, предложенное Л. Эйлером, в котором профили зубьев выполнены по эвольвентным кривым.

Эвольвентой окружности, называется траектория (кривая), которую описывает фиксированная точка производящей прямой K_yN_y, перекатывающейся без скольжения по неподвижной окружности (рис. 5.4).

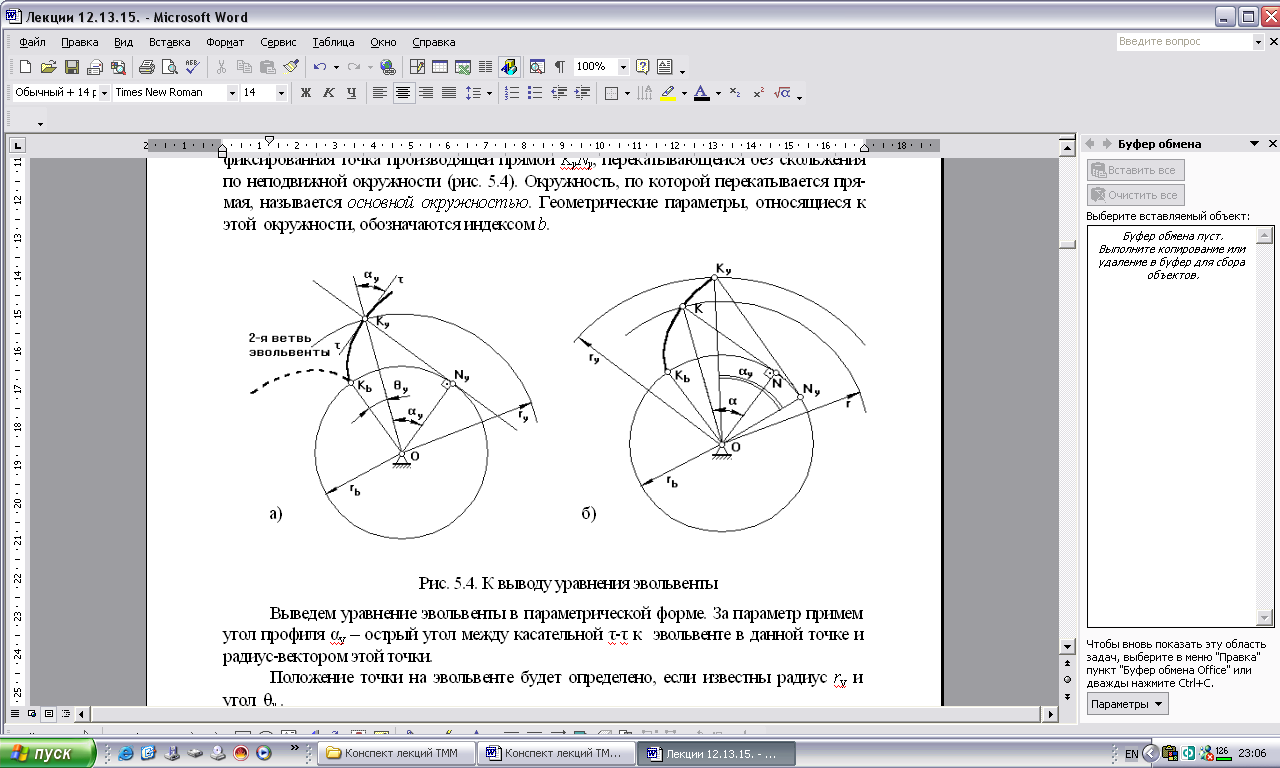
Рис. 5.4. К выводу уравнения эвольвенты

Окружность, по которой перекатывается прямая, называется основной окружностью. Геометрические параметры, относящиеся к этой окружности, обозначаются индексом b.

Выведем уравнение эвольвенты в параметрической форме.

За параметр примем угол профиля α_у – острый угол между касательной τ-τ к эвольвенте в данной точке и радиус-вектором этой точки.

Положение точки на эвольвенте будет определено, если известны радиус r_y и угол q_y .

Из треугольника ON_yK_y определим первое уравнение эвольвенты:

радиус произвольной окружности r_y равен (5.7).

Так как K_yN_y перекатывается без скольжения по основной окружности, то дуга K_bN_y равна отрезку K_yN_y или r_b (q_y + a_y) = r_b ^. tg a_y .

Откуда получаем второе уравнение эвольвенты:

inv a_y = q_y = tg a_y – a_y (5.8)

В теории зубчатых зацеплений угол q_y называют инволютой inv a_y.

a_у – угол профиля эвольвенты для точки K_у, лежащей на произвольной окружности.

a – угол профиля эвольвенты для точки K, лежащей на делительной окружности радиуса r.

Угол профиля эвольвенты для точки K_b, лежащей на основной окружности, равен нулю: a_b=0.

Радиус основной окружности равен r_b= r cos α = 0,5 m z cos α.

Свойства эвольвенты:

– Эвольвента начинается от основной окружности. Внутри основной окружности эвольвенты нет.

– Форма эвольвенты зависит от радиуса основной окружности. При стремлении радиуса r_b основной окружности к бесконечности, эвольвента превращается в прямую линию (пример рейка).

– Производящая прямая K_yN_y является нормалью к эвольвенте в данной точке.

– Нормаль к эвольвенте является касательной к основной окружности.