4.3.3. Алгоритмы силового расчета групп Ассура 2-го класса

Алгоритмы силового расчета группы Ассура 2-го класса различных видов представлены в нижеследующей табл. 4.1.

Таблица 4.1

Алгоритмы силового расчета групп Ассура 2-го класса .

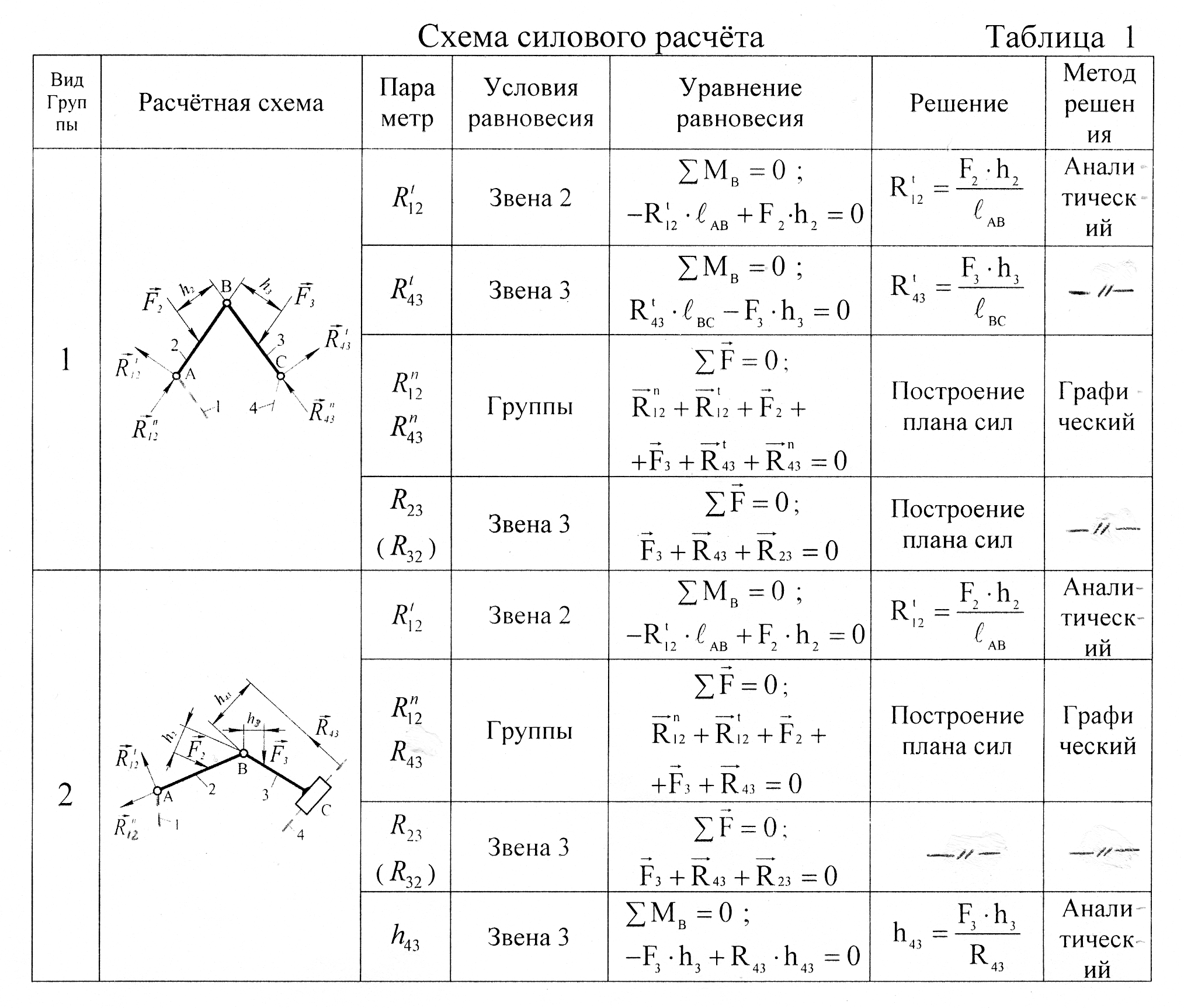
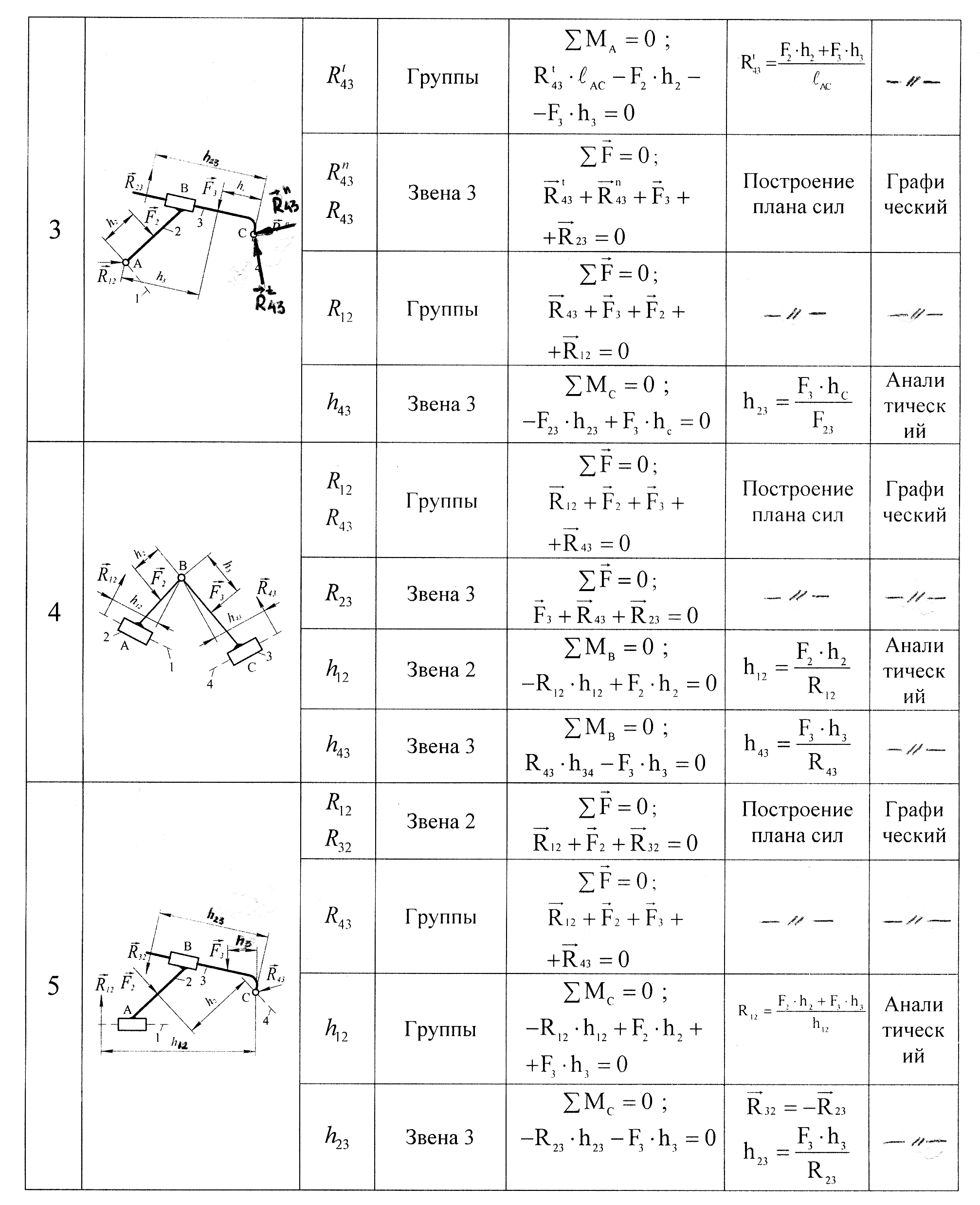
Сначала определяются все активные силы (силы тяжести звеньев, силы технологического сопротивления), а также силы и моменты сил инерции звеньев. Векторы этих сил прикладываются на план группы Ассура вычерченный в масштабе. В табл. 4.1 эти силы заменены их равнодействующими F₁ и F₂.

Затем прикладываются составляющие неизвестных реакций R₁₂ , R₄₃ , R₂₃ в кинематических парах. Далее определяются неизвестные величины и направления реакций.

Лекция 6

4.4. Силовой расчет начального звена

В результате силового расчета всех групп, образующих механизм, была определена сила _1-2 воздействия кривошипа на смежное с ним звено.2. Сила действия звено 2-го звена на кривошип 1 равна

_2-1 = – _1-2.

Движение начального звена 1 рабочей машины осуществляется двигателем через пару зубчатых колес (рис. 4.8,а), или при помощи муфты (рис. 4.8,б). В.первом случае воздействие привода на кривошип осуществляется уравновешивающей силой _y, приложенной в полюсе зацепления P под углом зацепления α, во втором случае – уравновешивающим моментом M_y.

а

б

Рис. 4.8. Действие уравновешивающей силы F_y или уравновешивающего момента M_y на начальное звено: а – схема с передачей движения через зубчатые колеса; б – схема с передачей движения через муфту.

Рассмотрим первый случай, когда движение начального звена 1 осуществляется двигателем, через пару зубчатых колес (рис. 4.9,а). Звено вращается с угловым ускорением ε₁.

Уравновешивающую силу определяем из уравнения равновесия ведущего звена, приравняв к нулю сумму моментов всех сил относительно точки O:

∑М_О = М_и + μ_S (– F_2-1 h₁ – G₁ h₃ + F_и1 h₂ + F_у h_у) = 0.

Откуда F_у = [ F_2-1 h₁ + G₁ h₃ – F_и1 h₂ ) – (М_и / μ_S )] / h_у .

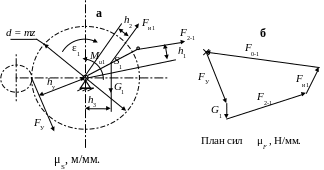
Рис. 4.9. Силовой расчет начального звена

Для определения F_0-1 построим план сил (рис. 4.9,б) в соответствии с векторным уравнением, соблюдая масштабный коэффициент μ_F :

∑ = _у + ₁ + _2-1 + _и1 + _0-1 =0.

4.4. Последовательность выполнения силового расчета

На рис. 4.10 показан механизм, состоящий из группы начальных звеньев, к которой присоединены группы Ассура ABCD и CE, с приложенными к ним силами. Установим последовательность силового расчета такого механизма.

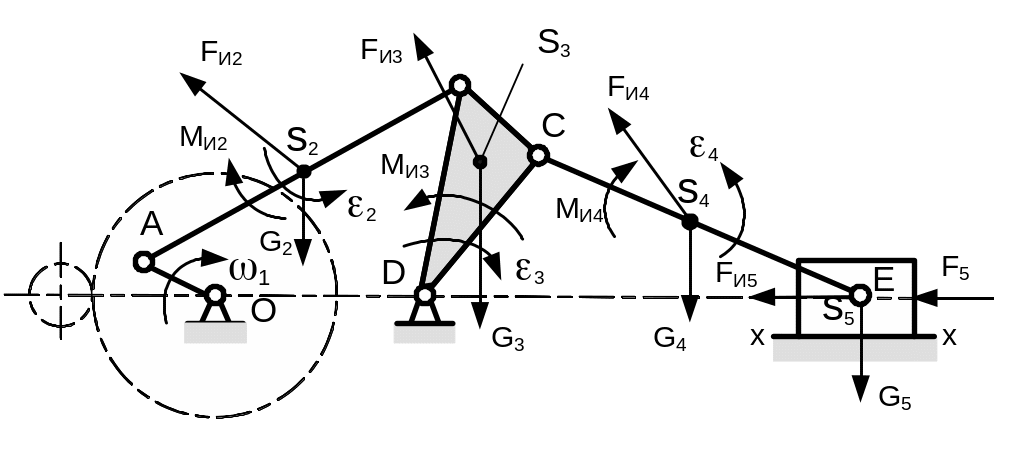Рис. 4.10. Кинематическая схема шестизвенного механизма, μ_S = 0,01 м/мм .

Если начать расчет механизма с начального звена ОА, то неизвестными окажутся силы в парах O и А. Кроме того, будет неизвестна уравновешивающая сила F_у, приложенная в зацеплении зубчатых колес. Таким образом, будет 5 неизвестных, так как векторы реакций в парах О и A определяются двумя неизвестными параметрами дают каждый (величиной и направлением). Для определения этих неизвестных можно составить только три уравнения статики, рассмотрев равновесие сил, приложенных к звену ОА. Следовательно, начинать расчет с начального звена нельзя. Если же начать силовой расчет с группы АВСD, то можно составить только 6 уравнений статики, неизвестных же будет 8 – составляющие реакций в парах A, В, С и D. Поэтому начинать силовой расчет с этой группы также нельзя.

Остается последняя группа СЕ, рассмотрев которую найдем векторы реакций _3-4 и _0-5 в парах С и Е. Это уже дает возможность решить задачу силового расчета группы AВСD, так как реакция _4-3 в паре C равна и противоположно направлена вектору _3-4. Затем можно переходить к расчету ведущего звена.

Следовательно, устанавливается вполне определенная последовательность силового расчета механизма. Начинается расчет с последней группы в порядке присоединения их к механизму 1-го класса, затем ведется расчет предпоследней группы и т. д. и заканчивается ведущим звеном.