Аналитические способы задания движения точки в пространстве
Линия, описываемая движущейся точкой в пространстве, называется траекторией. Она может быть прямолинейной или криволинейной. Движение точки считается заданным, если для любого момента времени можно указать все кинематические параметры движения: положение по отношению к системе отсчета, траекторию, скорость, ускорение.
Векторно-координатный способ задания движения точки
П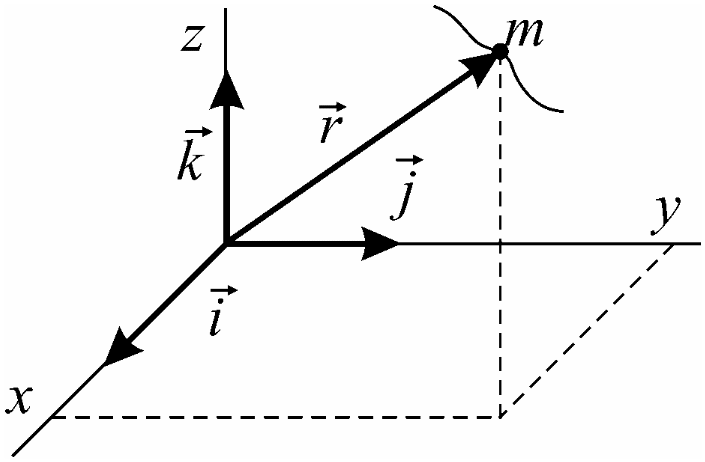
усть
точка m совершает
движение по отношению к прямоугольной
системе координат xyz.
Для определения положения точки в этой
системе необходимо знать три ее координаты
.
Если эти координаты известны для любого
момента времени, то движение точки
считается заданным, то есть координаты
заданы в виде известных функций времени:
. (1)
Система уравнений (1) представляет собой уравнения движения точки в декартовой системе координат.
Функции времени
однозначны (точка в одно и то же время
не может находиться в других точках
пространства), непрерывны (бесконечно
малому приращению времени t
соответствует бесконечно малое приращение
координат) и должны допускать производные.
Положение точки m в
пространстве может быть определено
радиусом-вектором
,
определяющим ее положение относительно
некоторой точки пространства:
.
Приняв за начало радиуса-вектора
начало координат системы xyz,
всегда можно выразить
через его проекции на оси координат:
,
где
– единичные орты координатных осей;
x,
y, z
– координаты точки m,
равные проекциям вектора
на соответствующие оси.
Величина радиуса
вектора равна
,
а направление его определяют направляющие
косинусы:
;
;
.
Очевидно, если задана
система уравнений (1), то можно определить
,
и наоборот. Уравнения
(1) могут рассматриваться как параметрические
с параметром t. При
переходе от параметрических уравнений
к уравнениям, связывающим
координаты (путем исключения параметра
t), получают уравнение
траектории точки. Например, из первого
уравнения выразим
и подставим в остальные:
Эти уравнения дают траекторию точки в виде линии пересечения двух поверхностей.
Естественный способ задания движения точки
П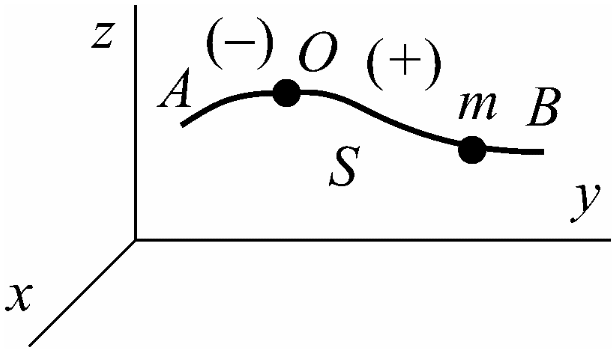
ри
естественном способе задания движения
задана траектория движения точки m
в системе отсчета xyz.
Движение точки будет считаться заданным,
если мы сможем в каждый
момент времени указать ее положение на
траектории.
Возьмем на траектории
точку
и назовем ее началом
отсчета. Измерим длину дуги
(со знаком + или –). Длину дуги S
называют дуговой координатой точки
m. Заданием дуговой
координаты
для любого момента времени однозначно
определяется положение точки на ее
траектории.
– уравнение движения точки при
естественном способе задания движения
или закон движения точки.
Примечание: не следует путать пройденный путь и дуговую координату, так как в общем случае это не одно и то же. Путь всегда положителен, а координата нет. При движении по замкнутой траектории путь по модулю не равен координате.
Определение скорости точки при различных способах задания движения
Под скоростью точки подразумевается быстрота изменения радиуса-вектора или дуговой координаты точки, определяющей ее положение.