Условие равновесия пар

Так как взятую систему пар, расположенных в одной плоскости, можно заменить одной парой, то для равновесия такой системы необходимо и достаточно, чтобы момент результирующей пары равнялся нулю:

.

Момент силы относительно центра

Пусть дана сила F и точка O. Опустим из точки O перпендикуляр на линию действия силы F. Перпендикуляр h называется плечом действия силы F.

Моментом силы относительно произвольно выбранного центра называется векторное произведение радиуса-вектора точки приложения силы на вектор самой силы.

Величина момента силы F относительно центра (точки) O равна взятому со знаком плюс или минус произведению величины силы на длину плеча:

.

Знак «+» в случае, если мысленный поворот тела от действия силы происходит против часовой стрелки; знак «–» – по часовой стрелке.

Точка (центр), относительно которой определяется момент силы, называется моментной.

Момент силы относительно точки равен нулю, если плечо силы равно нулю ( ), т.е. моментная точка лежит на линии действия силы.

Плоская система сил

Теорема Пуансо о переносе силы. Всякая сила, приложенная в данной точке A, эквивалентна той же самой силе, приложенной в другой точке B и паре с моментом, равным моменту силы, приложенной в точке A, относительно точки B.

Доказательство. Пусть задана сила , приложенная в точке A. В произвольной точке B приложим уравновешенную систему ( , ), эквивалентную нулю, причем . Таким образом, силы и  образуют пару. Итак, сила эквивалентна и паре ( , ), причём момент пары равен моменту силы относительно точки B.

Эта теорема позволяет привести все силы, действующие в плоскости, к одному центру.

Приведение произвольной плоской системы сил к данному центру

Выберем точку O и назовем её центром. Пользуясь предыдущей теоремой, перенесём все силы, действующие на тело в точку O. Получим систему сходящихся сил и некоторое количество пар. Сложив полученную систему сил по известному правилу силового многоугольника, получим одну силу , называемую главным вектором системы:

.

Складывая пары, получим результирующую пару с моментом, равным алгебраической сумме моментов слагаемых пар. Обозначив момент результирующей пары m, а моменты слагаемых пар , получим: .

Однако ранее доказано, что

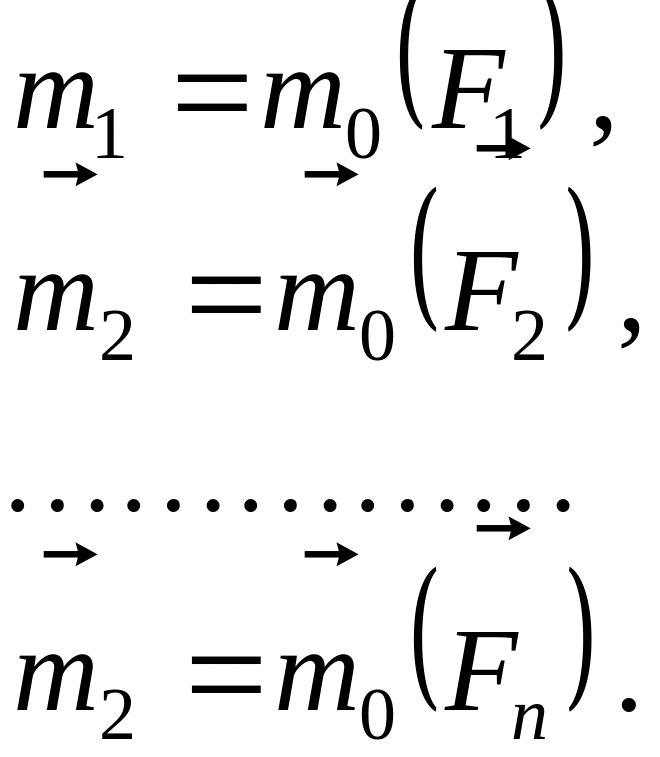
Следовательно, .

Эта сумма моментов всех сил относительно какого-либо центра приведения называется главным моментом системы.

В сякую плоскую систему сил всегда можно заменить одной силой, равной главному вектору системы и приложенной в произвольно выбранном центре приведения, и парой с моментом, равным главному моменту системы относительно выбранного центра приведения.

Важно отметить, что сила не является равнодействующей системы, т.к. она замещает систему только в совокупности с главным моментом.

Для аналитического определения главного вектора проведем оси координат и спроецируем уравнение на эти оси:

Направление главного вектора определяют направляющие косинусы:

.

Теорема Вариньона

Момент равнодействующих сил, расположенных в одной плоскости, относительно некоторой точки равен алгебраической сумме моментов составляющих сил относительно той же точки.

Доказательство.

П роанализируем характер распределения площадей:

2 площади ;

2 площади ;

2 площади .

Следовательно, .

Умножив уравнение на два, получим: .

Это равенство справедливо также и в векторной форме:

,

где знак «+» следует понимать в алгебраическом смысле.