Моменты инерции некоторых тел

1. Тонкий однородный стержень длиной l и массой м.

Найдем момент инерции относительно оси Az.

Для любого отрезка dx величина h = x, а масса , где  = M/l – масса единицы длины стержня.

.

Подставляя значение , получим .

2. Тонкое круглое однородное кольцо радиусом r и массой м.

Все точки кольца равноудалены от его центра C, следовательно:

.

Таким образом, .

Таким же будет результат и для цилиндрической оболочки.

3. Круглая однородная пластина (диск).

Выделим элементарное кольцо радиусом r, шириной dr . Площадь кольца S = 2∙r∙dr. , где , тогда .

Интегрируя, получим

.

Подставив значение , получим .

Момент инерции тела относительно параллельных осей

Теорема Гюйгенса. Моменты инерции данного тела относительно разных осей будут, в общем случае, разными. Зная J_С относительно одной оси, можно найти J_О относительно другой, ей параллельной.

Проведем оси через центр масс С и оси x, y, z, параллельные осям , через произвольную точку O , лежащую на оси .

Пользуясь формулами (3), запишем:

.

Из рисунка видно, что

.

Тогда

,

; ; .

Т.к. точка С является центром тяжести, то

Следовательно, третья сумма равна нулю, тогда

.

Итак, теорема Гюйгенса формулируется следующим образом: момент инерции тела относительно данной оси равен моменту инерции относительно центральной оси, ей параллельной, сложенному с произведением массы всего тела на квадрат расстояния между осями.

Очевидно, что , следовательно, момент инерции тела, относительно оси, проходящей через центр масс, будет наименьшим для всех осей данного направления.

Лекция 10 теорема об изменении количества движения механической системы

Количество движения точки и механической системы и его вычисление через скорость центра масс. Теоремы об изменении количества движения точки и системы

Количеством движения материальной точки называется векторная величина , равная произведению массы точки на вектор ее скорости.

Единица измерения – кг·м/с или Н·с.

Элементарным импульсом силы называется векторная величина , равная произведению вектора силы на элементарный промежуток времени :



Импульс силы за некоторый промежуток времени t₁ равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до t₁. Если сила F постоянна по модулю и направлению, то . В общем случае модуль может быть вычислен по его проекциям на координатные оси:

; ; .

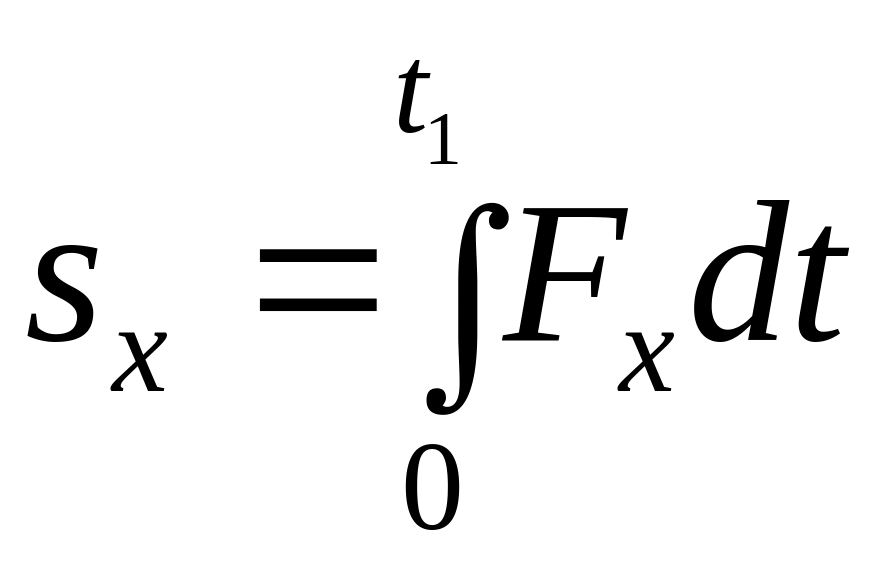Единица измерения [s] – Нс = кг·м·с/с² = кг·м/с.

По второму закону Ньютона,

,

а т.к. , то .

Таким образом, теорема об изменении количества движения материальной точки в дифференциальной форме формулируется в следующем виде: производная по времени от количества движения точки равна сумме действующих на нее сил.

Умножим обе части равенства на dt и проинтегрируем:

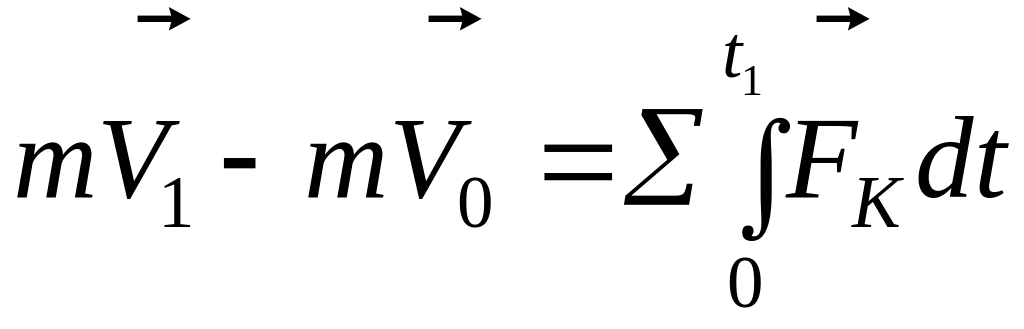
или

.

Теорема об изменении количества движения материальной точки в интегральной форме: изменение количества движения за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.

Количеством движения механической системы называется векторная величина , равная геометрической сумме (главному вектору) количеств движения всех точек системы:

.

Радиус-вектор центра масс:

или

.

Продифференцируем левую и правую части этого уравнения по времени:

.

Следовательно, .

Количество движения системы равно произведению массы всей системы на скорость ее центра масс.

Очевидно, что при V_C = 0, Q = 0, например, при вращении тела относительно оси, проходящей через центр масс тела.

Если движение тела сложное или плоскопараллельное, то количество движения Q не зависит от вращательного движения вокруг центра масс (например, колесо катится по рельсу). Количество движения – характеристика поступательного движения тела, а при сложном движении – характеристика поступательной части движения вместе с центром масс.

Рассмотрим систему из n материальных точек. Составим уравнения движения для каждой точки и сложим их:

.

Т.к. (свойство внутренних сил), то

. (1)

Производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил.

В проекциях на оси координат выражение (1) записывается в виде:

, , .

Разделив переменные и взяв интеграл, получим запись теоремы об изменении количества движения в конечной форме:

или

. (2)

В проекциях на координатные оси выражение (2) записывается в виде:

При решении задач о движении твердого тела удобнее пользоваться теоремой о движении центра масс . Однако в задачах с газами, жидкостью, реактивным движением и ударом целесообразнее пользоваться теоремой об изменении количества движения .