І частина

1. Б)

2. А)

3. Г)

4. А)

5. В)

Іі частина

6. .

Розв’язання:

1) ;

2) ;

3) .

Відповідь: .

7. .

;

;

;

.

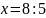Відповідь: .

Ііі частина

8. Розв’язання:

Нехай х см – друга сторона трикутника, тоді 2х см – перша сторона трикутника, а х + 5 см – третя сторона трикутника. За умовою задачі периметр дорівнює 85 см. Отже,

х + 2х + х + 5 = 85;

4х = 80;

х = 80 : 4;

х = 20 (см) – друга сторона трикутника.

Тоді, 20 ∙ 2 = 40 (см) – перша сторона трикутника.

20 + 5 = 25 (см) – третя сторона трикутника.

Відповідь: 40 см, 20 см, 25 см.

Варіант 14

І частина

1. В)

2. Г)

3. Г)

4. Б)

5. А)

Іі частина

6. .

Розв’язання:

1) ;

2) ;

3) .

Відповідь: .

7. ;

;

;

.

Відповідь: .

Ііі частина

8. Розв’язання:

Нехай х см – третя сторона трикутника, тоді 3х см – перша сторона трикутника, а 3х + 2 см – друга сторона трикутника. За умовою задачі периметр дорівнює 65 см. Отже,

х + 3х + 3х + 2 = 65;

7х = 63;

х = 63 : 7;

х = 9 (см) – третя сторона трикутника.

Тоді, 9 ∙ 3 = 27 (см) – перша сторона трикутника.

27 + 2 = 29 (см) – друга сторона трикутника.

Відповідь: 27 см, 29 см, 9 см.

Варіант 15

І частина

1. А)

2. Б)

3. Г)

4. Б)

5. В)

ІІ частина

6. .

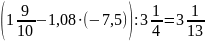Розв’язання:

1. ;

2. ;

3. .

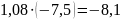Відповідь: .

7. ;

;

;

;

;

.

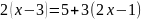Відповідь: .

ІІІ частина

8. Розв’язання:

1. 42 + 2,4 = 44,4 (см) – друга сторона трикутника.

2. 44,4 + 42 = 86,4 (см) – сума довжин першої та другої сторін трикутника.

3. 86,4 ∙ 0,35 = 30,24 (см) – третя сторона трикутника;

4. 44,4 + 42 + 30,24 = 116,64 (см) – периметр трикутника.

Відповідь: 116,64 см.

Варіант 16

І частина

1. Г)

2. А)

3. А)

4. Б)

5. В)

ІІ частина

6. .

Розв’язання:

1. ;

2. ;

3. .

Відповідь: .

7. ;

;

;

;

;

.

Відповідь: .

ІІІ частина

8. Розв’язання:

1. 6,8 ∙ 0,45 = 3,06 (см) – друга сторона трикутника.

2. 6,8 + 3,06 = 9,86 (см) – сума довжин першої та другої сторін трикутника.

3. 9,86 – 3,4 = 6,46 (см) – третя сторона трикутника;

4. 6,8 + 3,06 + 6,46 = 16,32 (см) – периметр трикутника.

Відповідь: 16,32 см.

Варіант 17

І частина

1. Б)

2. Г)

3. Б)

4. В)

5. А)

ІІ частина

6. .

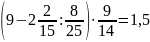Розв’язання:

1) ;

2) ;

3) .

Відповідь: .

7. Розв’язання:

;

При х = 12,4 та у = −7,6

.

Відповідь: .

ІІІ частина

8. Розв’язання:

Нехай х км/год – швидкість велосипедиста, тоді 3х км/год – швидкість мотоцикліста. За умовою задачі відстань між населеними пунктами 64 км, мотоцикліст і велосипедист зустрілися через 1,6 год. Отже,

(х + 3х) ∙ 1,6 = 64;

4х = 64 : 1,6;

4х = 40;

х = 40 : 4;

х = 10 (км/год) – швидкість велосипедиста.

3 ∙ 10 = 30 (км/год) – швидкість мотоцикліста.

Відповідь: 30 км/год.

Варіант 18

І частина

1. В)

2. В)

3. Б)

4. Г)

5. А)

Іі частина

6. .

Розв’язання:

1) ;

2) ;

3) .

Відповідь: 1,9.

7. Розв’язання:

;

При та

;

Відповідь: .

Ііі частина

8. Розв’язання:

Нехай х км/год – швидкість першого мотоцикліста, тоді х + 7 км/год – швидкість другого мотоцикліста. За умовою задачі відстань між містами 665 км, через 7 годин вони зустрілися. Отже,

(х + х + 7) ∙ 7 = 665;

2х + 7 = 665 : 7;

2х + 7 = 95;

2х = 95 – 7;

2х = 88;

х = 88 : 2;

х = 44 (км/год) – швидкість першого мотоцикліста.

44 + 7 = 51 (км/год) – швидкість другого мотоцикліста.

Відповідь: 44 км/год; 51 км/год.

Варіант 19