6. Решение слау методом Гаусса

Написать функцию, которая находить решение системы методом Гаусса. Найти решение системы при помощи данной функции. Проверить результат.

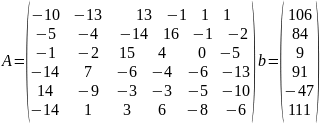
Заполнение матриц происходит с помощью функции Матрица или вектор (Панель векторов и матриц→матрица или вектор) (рисунок 1.13).

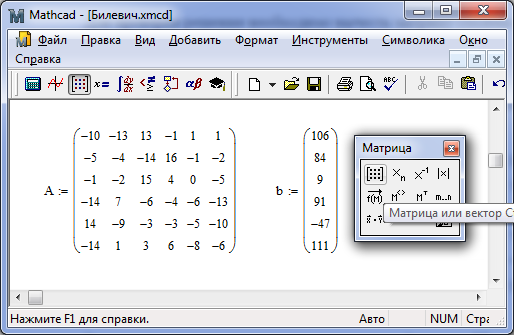
Рисунок 1.13 – Заполнение матриц

С помощью элементов программирования создается функции для решения СЛАУ методом Гаусса. Объединение матриц aиbпроисходить с помощью функции augment. Затем, основная матрица сводиться к единичной при помощи функции rref. Результатом является матрица-столбец значений соответствующих неизвестных, выделенная из последнего столбца расширенной матрицы (рисунок 1.14).

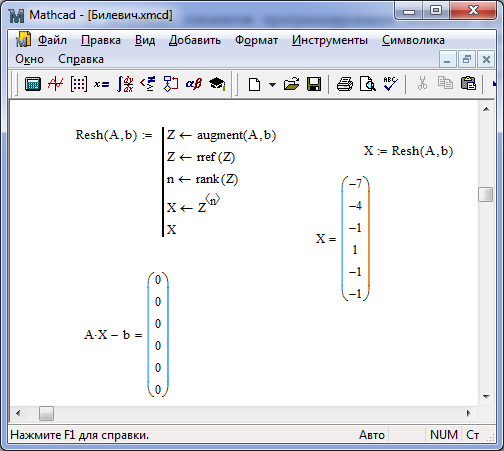
Рисунок 1.14 – Решение СЛАУ методом Гаусса

Для проверки решения необходимо вычесть матрицу столбец из произведения исходной матрицы А и полученной матрицы.

7. Матричные операции

1. Определитель матрицы. Размерность матрицы подбирать с учетом выражения. Количество строк и столбцов исходных матриц – не менее четырех. Обязательно наличие неквадратных матриц.

2. Заполнить матрицы случайными значениями при помощи встроенных функций (не вручную).

3. Вычислить заданное матричное выражение.

4. Для результирующей матрицы выполнить следующее:

1. сложить каждый элемент со скаляром x1;

2. вычесть каждый элемент со скаляром x2;

3. вычислить определитель матрицы;

4. найти обратную матрицу и проверить результат;

5. найти собственные числа и собственный вектора и проверить результат;

6. вычислить ранг матрицы;

7. определить вектора, которые состоят из элементов n-строки и m-столбца и для них вычислить;

• Модуль каждого вектора

• Орт каждого вектора

• Сумму координат

• Количество положительных и отрицательных координат каждого вектора

• Скалярное произведение векторов

• sin(γ),cos(γ), где γ – угол между векторами4

• Векторное произведение

• Вектор, координаты которого являются произведением соответствующих координат векторов

Таблица 1.1 – Необходимые значения для матричных операций

Выражение	X1	X2	n	m
(DA-DO)+BE	25.45	69.54	3	4

Задаем переменные диапазонного значения для описания размера исходных матриц: n=0..2; m=0..3.

Матрицы, требуемые для решения, заполняются случайными целыми значениями.

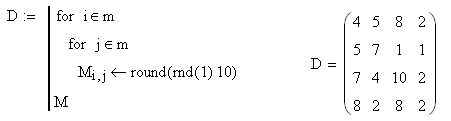
Чтобы вычислить значения искомой матрицы, необходимо присвоить данное выражение новой переменной и вывести значение этой переменной.

Для выполнения математических операций (сложения матрицы со скаляром, вычитания скаляра из матрицы) нужно использовать простой синтаксис сложения (вычитания).

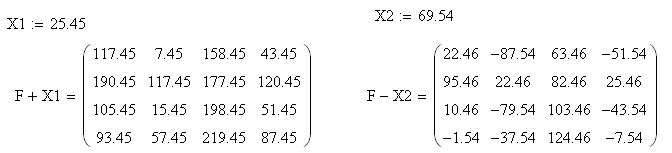
Вычисление определителя выполняется с помощью встроенной функции MathCAD.

Найти обратную матрицу можно с помощью стандартной функции. Проверка осуществляется перемножением исходной матрицы и полученной. Результатом является единичная матрица

Найти собственные числа и собственные вектора матрицы можно с помощью встроенных функций MathCAD (eigenvals, eigenvecs).

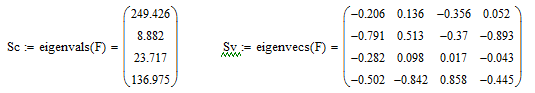
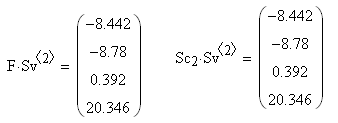
Чтобы проверить результат предыдущего действия, необходимо перемножить матрицу на каждый собственный вектор и сравнить результат с произведением этого собственного вектора на соответствующее собственное число.

Также с помощью встроенной функции rank можно найти ранг матрицы.

Для определения векторов состоящих из элементов n-строки иm-столбца, нужно задать номер строки n и номер столбца mтаким образом, чтобы эти числа намеренно были меньше на 1, так как нумерация элементов матрицы в пакете MathCAD начинается с 0. Для выбора строки необходимо воспользоваться встроенной функцией извлечения столбца матрицы в новую переменную типа, предварительно транспонировав матрицу. Для получения столбца матрицу транспонировать не нужно.

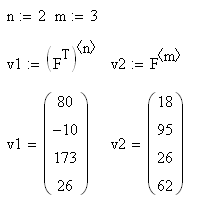
Для нахождения модуля (длины) вектора нужно использовать встроенную функцию Абсолютное значение(Панель инструментов «Калькулятор» → Абсолютное значение) (рисунок 1.15).

Рисунок 1.15 – Нахождение длин векторов

Орт вектор – это вектор единичной длины в направлении исходного вектора. Чтобы его вычислить, необходимо создать функцию ort с помощью элементов программирования. При этом поделим каждую координату вектора на его длину.

Чтобы подсчитать суммы координат, нужно создать функцию, инициализировав переменную S, в которой будет сохраняться результат. Необходимо перебирать координаты векторов и суммировать из них в переменную S.

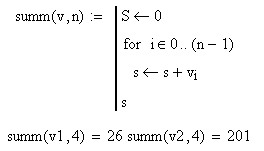
Для подсчета количества положительных и отрицательных координат каждого вектора необходимо создать функции posиnegсоответственно. Эти функции похожи на предыдущую функцию, только вместо суммирования всех координат, значение переменной увеличивается на 1, если текущие координаты положительны для функции pos или отрицательны для функции neg.

Для нахождения скалярного произведения векторов нужно перемножить их с помощью простой операции «умножения».

Вычислить cos(y) можно с помощью преобразования формулы (2), выразив из неё cos(y).

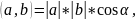(2)

где α – угол между векторами.

Вычислить sin(y) можно, выразив его из основного тригонометрического тождества, зная значениеcos(y). Для нахождения векторного произведения нужно воспользоваться формулой 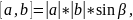(3).

(3)

где α – угол между векторами.

Чтобы получить вектор из произведения координат исходных векторов, нужно создать функцию vector.

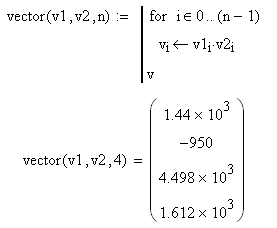
Вектор в MathCAD – это одномерный массив, который можно обрабатывать как с помощью встроенных функций пакета MathCAD, так и при помощи созданных пользователем функций, каждая из которых ссылается на отдельную координату вектора с помощью подстрочных индексов.