Функциональная спецификация модели парной регрессии.
Функциональными называются связи, при которых наличие взаимосвязи между двумя переменными, означает, что любому заданному значению одной переменной отвечает лишь одно значение второй.
Для них характерно то, что изменения результативного признака в целом обусловлены действием факторного признака х: Y=f(X)
Особенность функциональной связи: она проявляется с одинаковой силой для каждой единицы совокупности, которая изучается.
Поэтому, установив при изучении любой единицы совокупности ту или другую закономерность, ее можно распространять как на каждую единицу, так и на всю совокупность.
Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки (выбора) вида модели, исходя из соответствующей теории связи между переменными.
Линейная
регрессия: 
.
граничения модели множественной регрессии.
Предположим,
что связь между объясняемой переменной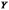 
и
объясняющими переменными 
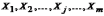линейная,
т.е.
.
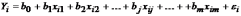Пусть выполняются следующие условия:
1) 
, 
;
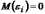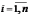2) 
,
для любых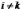 
;
3) 
,
,
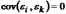4) 
, 
,
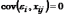т.е. распределение 
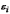не
зависит от распределения любой объясняющей
переменной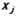 
;
5) ошибки имеют нормальный закон распределения, ;
6) 
,
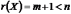т.е. ранг матрицы 
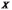должен
быть равен числу оцениваемых параметров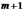 
,
что означает отсутствие линейной
зависимости между объясняющими
переменными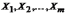 
.
Тогда
МНК-оценка вектора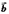 
: 
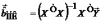имеет
наименьшую дисперсию в классе всех
линейных несмещенных и состоятельных
оценок.
Условия Гаусса-Маркова 1)-6) называются предпосылками МНК для случая множественной линейной регрессии.
дентификация параметров множественной регрессии МНК.
Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.
Ввиду четкой
интерпретации параметров наиболее
широко используется линейная функция.
В линейной множественной регрессии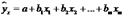 
параметры
при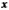 
называются
коэффициентами «чистой» регрессии. Они
характеризуют среднее изменение
результата с изменением соответствующего
фактора на единицу при неизмененном
значении других факторов, закрепленных
на среднем уровне.
Рассмотрим линейную модель множественной регрессии
.
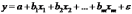(2.1)
Классический
подход к оцениванию параметров линейной
модели множественной регрессии основан
на методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки
параметров, при которых сумма квадратов
отклонений фактических значений
результативного признака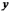 
от
расчетных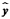 
минимальна:
.
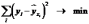(2.2)
Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.
Итак. Имеем
функцию 
аргумента:
.
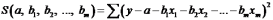Находим частные производные первого порядка:
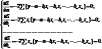
После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (2.1):
(2.3)
Для двухфакторной модели данная система будет иметь вид:
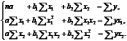
ценка статистической значимости множественного уравнения регрессии, F-критерий Фишера.
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
Частный
F-критерий оценивает статистическую
значимость присутствия каждого факторов
в уравнении. В общем виде для
фактора 
частный
F-критерий определится как
пецификация модели множественной регрессии. Свойства множественных коэффициентов регрессии.
Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.
Вид множественной линейной модели регрессионного анализа:
Y = b0 + b1xi1 + ... + bjxij + ... + bkxik + ei
где ei - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.
Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной.
Экономический смысл параметров множественной регрессии Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом.