
- •Метод наименьших квадратов.
- •Свойства коэффициентов регрессии.
- •Нелинейная регрессия. Методы линеаризации.
- •Приведение к линейному виду регрессий, нелинейных по объясняющим переменным
- •Приведение к линейному виду регрессий, нелинейных по параметрам
- •Функциональная спецификация модели парной регрессии.
- •Матричная запись множественной линейной модели регрессионного анализа:
- •Истемы регрессионных (одновременных) уравнений.
- •Структурная и приведенная формы модели.
- •Модели распределенных лагов.
Метод наименьших квадратов.
Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методоврегрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.
Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.
Свойства коэффициентов регрессии.
В
практике эконометрического анализа
чаще всего используют линейную парную
регрессию (функциональная зависимость
1). Уравнение регрессии будем искать в
виде 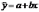 .
Неизвестные (пока) коэффициенты
.
Неизвестные (пока) коэффициенты 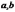 являются
оценками параметров
являются
оценками параметров  .
Можно сказать, что эмпирическое уравнение
регрессии
является оценкой
по выборке регрессионной
модели
.
Можно сказать, что эмпирическое уравнение
регрессии
является оценкой
по выборке регрессионной
модели 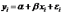 .
.
Метод наименьших квадратов для линейной парной регрессии состоит в следующем:
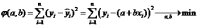 ,
,
где 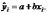
Вычисляя
производные по параметрам 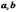 и
приравнивая их к нулю, приходим к
следующей системе из двух уравнений
и
приравнивая их к нулю, приходим к
следующей системе из двух уравнений

Решение системы уравнений называется оценкой неизвестных параметров по методу наименьших квадратов, его можно найти по формулам:

где
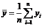 ,
,  ,
,  ,
, 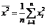 .
.
Используя понятия выборочных дисперсий, ковариаций и корреляций оценки наименьших квадратов (решение системы уравнений) можно записать специальным образом:
 ,
,  ,
,
где  ,
,  —
выборочные средние,
—
выборочные средние,
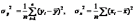 —
выборочные
дисперсии,
—
выборочные
дисперсии,
 —
выборочный
коэффициент корреляции.
—
выборочный
коэффициент корреляции.
Следовательно, парная эмпирическая линейная регрессия имеет вид
 .
.
Нетрудно найти значения показателя, рассчитанные по линейной регрессии для тех значений объясняющего фактора, которые содержатся в выборке
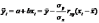 ,
, 
Особое значение для проверки статистической значимости парной линейной регрессии имеют остатки (разности между значениями показателя, полученными в эксперименте, и вычисленными по уравнению линейной регрессии):
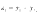
Вычисленному
коэффициенту  при
объясняющем факторе
при
объясняющем факторе  в
парной линейной регрессии можно дать
естественную экономическую интерпретацию.
Параметр b называется
коэффициентом регрессии. Его величина
показывает, насколько единиц изменится
результат с изменением фактора на одну
единицу.
в
парной линейной регрессии можно дать
естественную экономическую интерпретацию.
Параметр b называется
коэффициентом регрессии. Его величина
показывает, насколько единиц изменится
результат с изменением фактора на одну
единицу.
Параметр a,
вообще говоря, не имеет экономической
интерпретации. Формально  –
значение
–
значение 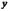 при
при 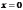 .
Например, если a<0,
то попытка его экономической интерпретации
приводят к абсурду.
.
Например, если a<0,
то попытка его экономической интерпретации
приводят к абсурду.
Зато можно интерпретировать знак при параметре а. Если, а>0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Нелинейная регрессия. Методы линеаризации.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др.
Различают два класса нелинейных регрессий:
регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:
· полиномы разных степеней –у = а +bх + с2 + е,
у =а + bх +сх +dx3+ е,
равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам относятся функции:
степенная — y = axbе
показательная – у = аbх е
экспоненциальная – y=ea+bxе
