Билет n19

1. Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.Эффект Доплера применим не только для звука но и для световых волн.

; где ν-воспринимаемая приемником; ν0-частота звука

1)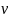 (ист)=0

(приемника )=0 =ƛ/ ν* ν0

2) (приемника )>0

(ист)=0

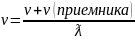
3) (ист)=0

v= (ист)*T)

4) (приемника )>0

(ист)>0

v=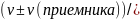 (ист))

2. Внутренняя энергия реального газа будем определяться суммой кинетической энергии Eк теплового движения его молекул и потенциальной энергии взаимодействия молекул между собой - Eп:

U=Eк+Eп.

Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие последних приводит к возникновению внутреннего давления p' на газ.Внутреняя энергия равна const.Следовательно -Eк= Eп - изменяя потенциальную энергию мы изменяем кинетическую, а следовательно и температуру.

Эффект Джоуля-Томсона:

Работа молекул газа против сил трения, в результате просачивания через перегородку, тратиться на изменение температуры газа. Охлаждение газа при расширении это положительный эффект Дж-Тм. Нагревание это отрицательный эффект.

Знак эффекта Дж-Тм зависит от того, какая из поправок играет большую роль в уравнении Вандервальса. Для одного и того же газа в зависимости от T и P может играть большую роль поправка А или В.Существуют такие параметры при которых роль поправок одинакова или такое состояние называется точки инверсии.

Билет n20

1.Корпускулярно – волновой дуализм. Гипотеза де-Бройля. Дифракция электронов.

Дифракция электронов — процесс рассеяния электрона на совокупности частиц вещества, при котором электрон проявляет волновые свойства. Данное явление называется корпускулярно-волновым дуализмом, в том смысле, что частица вещества(в данном случае взаимодействующие электроны) может быть описана, как волна. Таким образом Корпускулярно-волновой дуализм – принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.

Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону.

Соотношение де-Бройля:

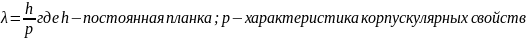
2.Идеальная жидкость. Уравнение Бернулли.

Идеальная жидкость - воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутреннее трение и теплопроводность.

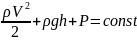- Уравнение Бернули для потока идеальной несжимаемой жидкости.

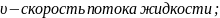
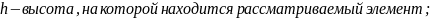
21. 1. Уравнение Шредингера. Волновая ф-ция и ее физический смысл.

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике. Установлено Эрвином Шрёдингером в 1926 году.

Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени :

Зависимое от времени уравнение (общий случай)

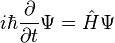
, где — гамильтониан.

В квантовой физике вводится комплекснозначная функция , описывающая чистое состояние объекта, которая называется волновой функцией

Пусть волновая функция задана в n-мерном конфигурационном пространстве, тогда в каждой точке с координатами , в определенный момент времени t она будет иметь вид . В таком случае уравнение Шрёдингера запишется в виде:

где , — постоянная Планка; — масса частицы, — потенциальная энергия в точке в момент времени , — оператор Лапласа

Волнова́я фу́нкция, или пси-функция — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

где — координатный базисный вектор, а — волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

В координатном представлении волновая функция зависит от координат системы. Физический смысл приписывается квадрату её модуля , который интерпретируется как плотность вероятности обнаружить систему в положении, описываемом координатами в момент времени :

.

Тогда в заданном квантовом состоянии системы, описываемом волновой функцией , можно рассчитать вероятность того, что частица будет обнаружена в любой области конфигурационного пространства конечного объема :

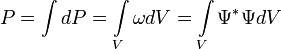
2.Вязкая жидкость. Формула Стокса. Формула Пуазейля.

Вязкая жидкость (Ньютоновская жидкость) - это жидкость в которой возникает трение во время движения

Простое уравнение, описывающее силы вязкости в ньютоновской жидкости, во многом определяющие ее поведение, основано на сдвиговом течении:

,

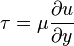где:

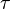• — касательное напряжение, вызываемое жидкостью, Па;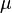

• — динамический коэффициент вязкости — коэффициент пропорциональности, Па·с;

• — производная скорости в направлении, перпендикулярном направлению сдвига, с⁻¹.

Закон Стокса описывает силу трения при движении в вязкой жидкости.

Где:

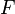• — сила трения, так же называемая силой Стокса,

• — радиус сферического объекта,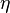

• — динамическая вязкость жидкости,

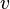• — скорость частицы.

Согласно Пуайзелю, объем вытекаемой вязкой жидкости через капилляр равен:

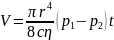
• V— объем жидкости,

• R - радиус капилляра,

• L— длина капилляра,

• — динамическая вязкость жидкости,

• p_1-p₂— перепад давления,

• t - время движения