12)Формула Байеса.

Предположим, что в результате эксперимента зафиксировано событие B. Тот факт, что событие B произошло, позволяет уточнить априорные вероятности гипотез (то есть, получить их апостериорные оценки). Это можно сделать с помощью формулы Байеса:

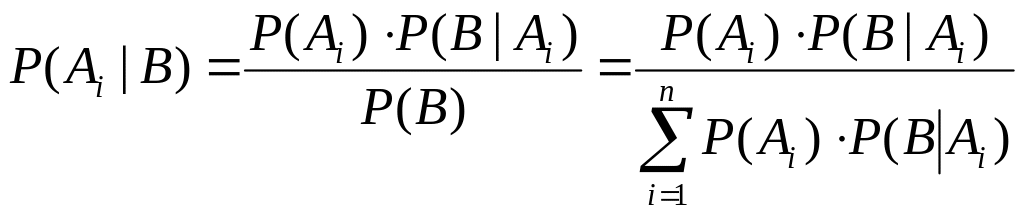
14)Классическая вероятность события и ее свойства.

Рассмотрим некоторый эксперимент, в котором совокупность элементарных событий {W1, W2,…,Wn} образует полную группу событий. Предположим, что в эксперименте фиксируется наступление(ненаступление) события А. Пусть среди n элементарных событий ровно m событий благоприятствуют событию А.

Опр. Классической вероятностью события А называется отношение m к n.

m-число благоприятствующих событию А элементарных событий, а n-число всех элементарных событий данного эксперимента, образующих полную группу.

Св-ва кл. вероят-ти:

1. Если в данном эксперименте событие А явл. достоверным событием, то его кл. вер-ть=1 . Действительно, т.к. достоверное событие обязано произойти в эксперименте, то для него любое элементарное соб-е из полной группы событий явл. благоприятствующим и значит вып-ся

2. Если А явл. невозможным событием в данном эксперименте, то его классическая вер-ть=0 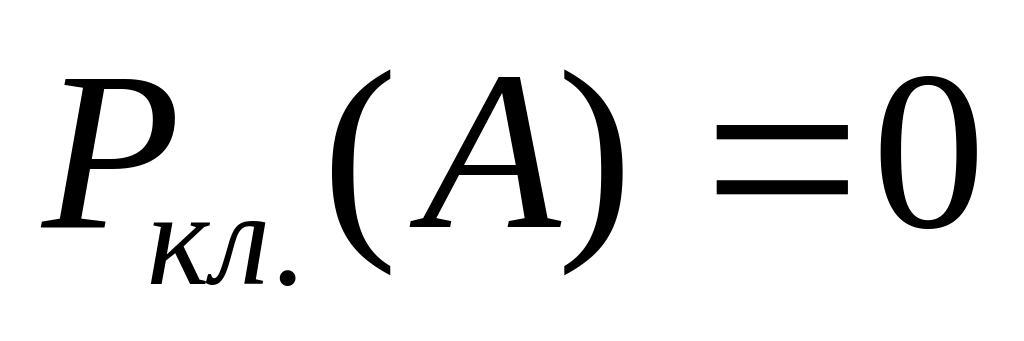. Действительно для невозможного события среди элементарных событий полной группы благоприятствующих ему событий нет, поэтому имеет:

3. Если А-случайное соб-е, то верно неравенство: 0< 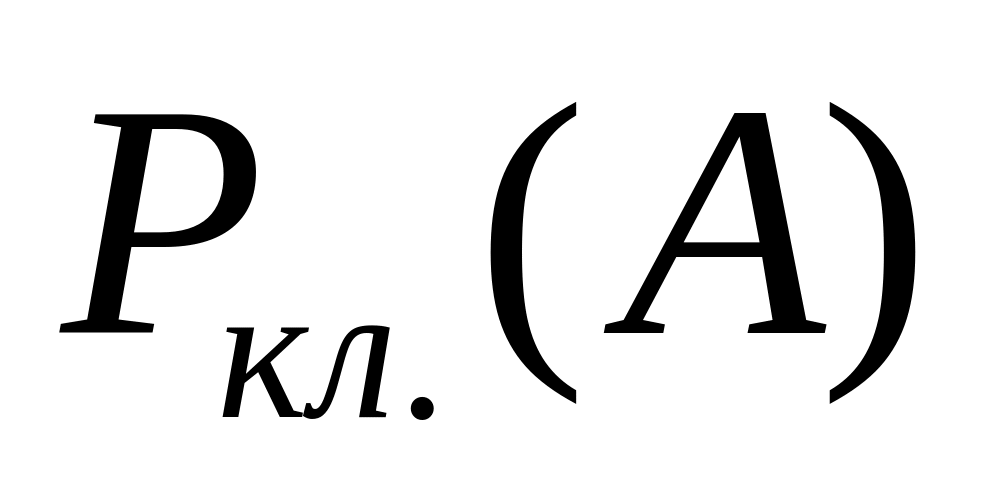<1

Замечание: Т. обр., для любого соб-я экспер-та вып-ся рав-во: 0≤ <1

15)Основные операции над событиями и их св-ва.

Опр. Пусть даны 2 события А и В. Объединением(суммой) этих 2-х событий называется соб-е (АÈB(A+B)), состоящее в том, что в рез-те экспер-та произойдет хотя бы одно из этих событий (т.е. произ. либо только соб-е А, либо-В, либо и А и В).

Замечание: Очевидно, что в том случае, когда соб-я А и В явл. несовместными, соб-е АÈB произойдет тогда, когда произойдет либо только соб-е А, либо только соб-е В.

Операция объединения 2-х событий легко обобщается на случай любого конечного числа событий.

Опр. Объединением соб. называется соб-е (А1ÈA2È…ÈAn=È(вверху n, внизу j=1)Aj), состоящее в том, то в рез-те экспер-та произошло хотя бы одно из этих событий.

Опр. Пусть даны 2 собы-я А и В. Пересечением(произведением) этих 2-х событий называется соб-е (А∩В(AB)), состоящее в том, что в рез-те экспер-та наблюдались оба этих соб-я.

Замечание: Операция произведения 2-х событий обобщается на любое конечное число событий.

Опр.Пусть в рез-те экспер-та могу произойти соб-я . Пересечением(произведением) этих событий называется соб-е (∩Ai), состоящее в том, что в рез-те экспер-та будут наблюдаться все эти соб-я.

Опр. Пусть в экспер-те могут наблюдаться соб-я А и В. Разностью событий А и В называется соб-е, обозначаемое либо A\B(A/B), состоящее в том, что в рез-те экспер-та соб-е А произошло, а соб-е В-нет.

Рассматриваемые операции обладают след. св-вами:

1. АÈВ=ВÈА-свойство коммутативности. А∩В= В∩А

2. АÈ(ВÈС)= (АÈВ)ÈС-св-во ассоциативности. А∩(В ∩С)= (А∩В )∩С

3. АÈ(В∩С)= (АÈВ)∩(АÈС)-св-во дистрибутивности

А∩(ВÈС)= (А∩В) È(А∩С)

Если обозначить через достоверное соб-е, а О-невозможное соб-е, -соб-е, противоположное к А, то верны равенства: , ,

=А, АÈ = , А∩О=О, АÈО=А.