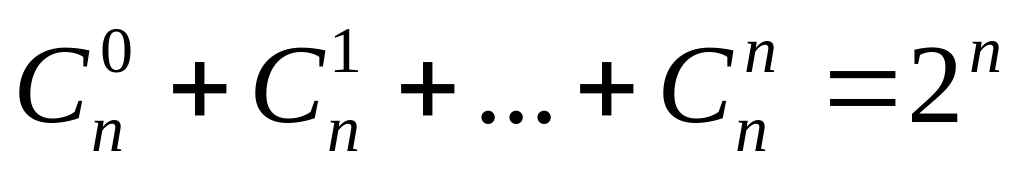1)Правило сложения. Общее правило сложения. Правило умножения. Общее правило умножения.

Пусть А-некоторое конечное множество, обозначим через n(A)-кол-во элементов данного множества. Если мн-во А-пустое, то число его элементов равно нулю. n(Æ)=0

Правило сложения. Если А,В–конечные непересекающиеся множества (А∩В=Æ), то число элементов их объединения равно сумме числа эл-тов мн-ва А и числа эл-тов мн-ва В. n(AÈB)=n(A)+n(B)

Правило сложения допускает следующее обобщения:

-Пусть A1, A2,…, An–конечные попарно пересекающиеся множества (Ai∩Aj=Æ "ij=1,n), тогда кол-во элементов в объединении этих множеств равно сумме n(А1)+n(A2)+…+n(An) или

n(AÈ(на верху n, а внизу i=1)Ai)=(значок суммы от i=1 до n)(Ai).

Пусть А и В-есть некоторые конечные множества. Декартовым произведением этих множеств называется множ-во A×В, элементами которого являются все двойки вида А×В={(а,b):aÎA, bÎB}.

Правило умножения. Число элементов в декартовом произведении множеств А и В равно произведению числа эл-тов множ-ва А на чило элементов множ-ва В. n(A×B)=n(A)*n(B).

Правило умножения допускает след. обобщения:

-пусть A1, A2,…, An-некот. конечные множ-ва, тогда кол-во элементов в декартовом произведении этих множеств равно произведению

n(A1×A2×…×An)=n(A1)*n(A2)*…*n(An)

Для практич. задач ТВ правила сложения формулируются так:

Правило сложения. Если первый из 2-х объектов может быть выбран способами, а второй объект может быть выбран другими способами, то выбор какого-то одного из этих объектов может быть осуществлен всего способами.

Правило умножения. Если первый из 2-х объектов может быть выбран способами и после каждого из таких выборов второй объект может быть выбран способами, то выбор сначала первого объекта, а затем второго объекта можно осуществить всего способами.

2) Вероятность заданного отклонения

Пусть дана случайная величина X(W)~N(a, cигма(с загагулиной)^2).

Зафиксировано некоторое положительное число d>0 и найдем вер-ть соб-я, состоящего в том, что в результате эксперимента случайная величина примет значение, отклоняющееся от своего математического ожидания на величину не большую чем d

d>0

P(|X(W)-a|<d)

Рассмотрим нер-во:

-d< X(W)-a<d

a-d<X(W) <a+d

Найдем вер-ть соб-я P(a-d< X(W) <a+d)=

a-d=альфа, a+d=бета

=|фи(бета-а/сигма с загагулиной)-фи(альфа-а/сигма с загагулиной)|=

=фи(а+d-а/ сигма с загагулиной)-фи(а-d-а/ сигма с загагулиной)=

=фи(d/сигма с загагулиной)-фи(-(d/сигма с загагулиной)=

=(т.к. ф-ция Лапласа нечетная)=2фи(d/сигма с загагулиной)

P(|X(W)-a|<d)=2фи(d/сигма с загагулиной)

Замечание: вследствие соотношение

P(|X(W)-a| ≥d)=1-2фи(d/сигма с загагулиной)

d-отклонение

а-мат. Ожидание

сигма с загагулиной-сред. кв. отклонение.

4)Размещения и их св-ва.

Рассмотрим следующую классическую задачу комбинаторики: пусть имеются ровно n различных объектов 1,2,...,n. Требуется подсчитать ск. сущ. различных способов выбора из них ровно m объектов, если порядок выбора существенен.

Теорема: Существует всего способов выбора m из n объектов, если порядок отбора существенен.

Замечание: Число принято обозначать и называть числом размещений из n по m. =

(a+b)^n=

С с индексами-это биноминальные числа.

Бинон-Ньютон обл. след. свойствами:

1. (n+1)-число слогаемых

2. биноминальные коеф-ты равноудаленные от начала и конца в сумме правой части равны друг другу

3. общий член разложения имеет вид

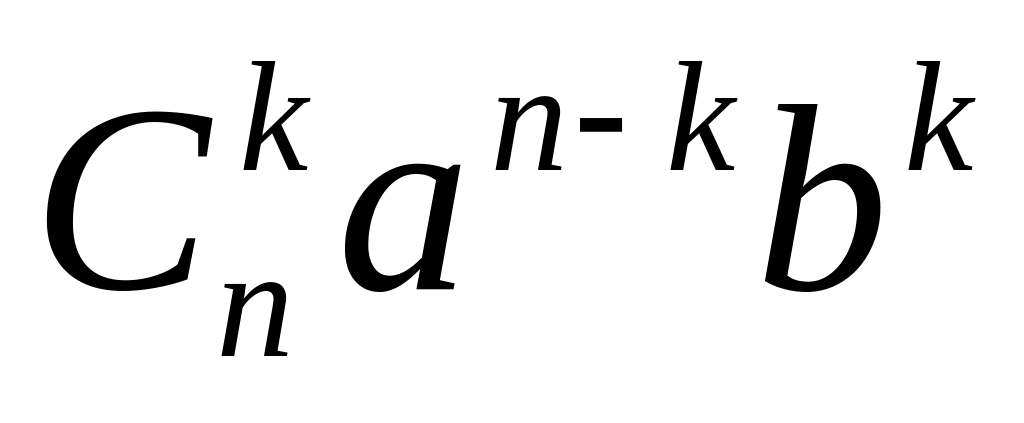
4. сумма всех биноминальных коэф-в равна