Метод падающего шарика

Метод пригоден для измерения вязкости жидкостей (рис.17).

а

б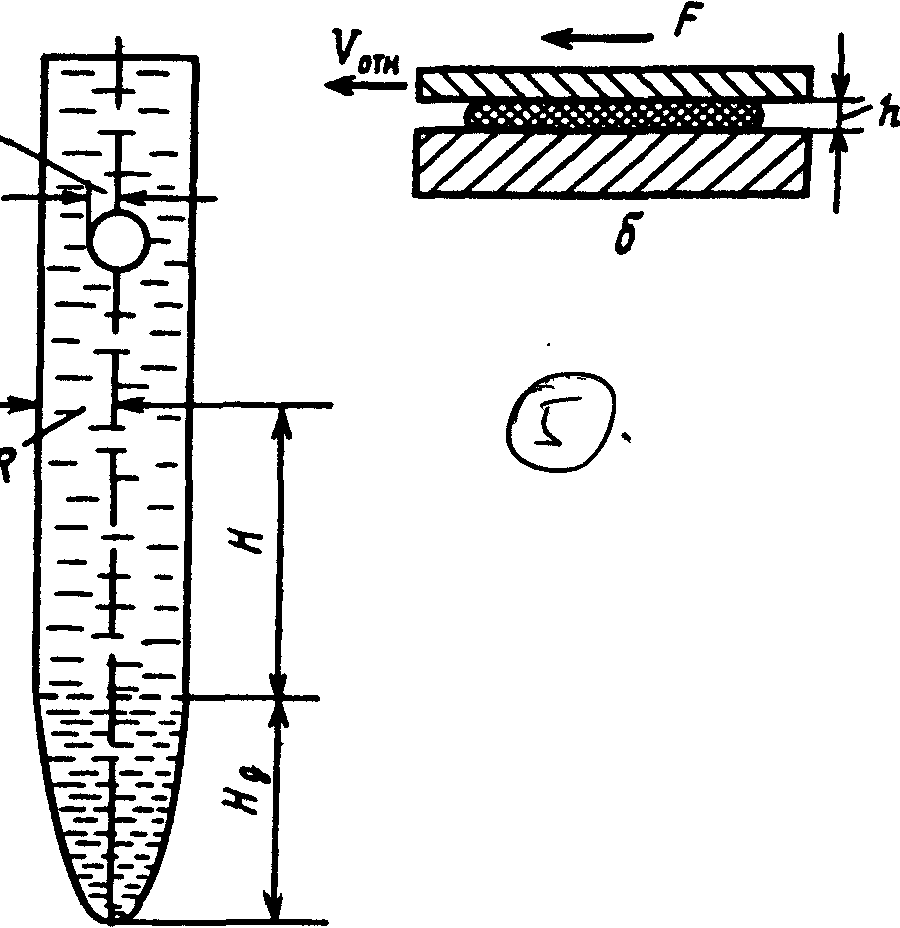

Рис. 17. Схемы шарикового (а) и плоскостного (б) вискозиметров:

а) R – радиус цилиндра; r – радиус шарика; Н – высота падения шарика со скоростью V; Н_д – расстояние от нижней метки до дна цилиндра;

б) V_отн – относительная скорость смещения плоскостей; F – приложенная сила; h – зазор

Вязкость жидкости (плотность которой ₀) определяют по установившейся скорости V падения шарика радиусом r из материала плотностью . При падении шарика по оси цилиндра в соответствии с формулой Стокса  Ладенбурга имеем

    rR  rR²  rR⁵К^1,

где     ₀gR²/V; K = 1 + 3,3R/H.

Это уравнение справедливо при r/R  0,32.

Максимальная скорость падения шарика должна удовлетворять требованию

(11)

где Re – критерий Рейнольдса.

Вместо оценки времени падения тарированного шарика на определенном пути можно вычислять время подъема пузырька газа через жидкость.

Метод сдвига параллельных плоскостей

Метод применяется для определения _эф в диапазоне 10ⁿПас, где n = 110 при малых  (см. рис. 17, б).

При движении плоских пластин относительно друг друга осуществляется простой сдвиг полимерного материала. При этом

(h/S₁₁)(F/V_отн), (12)

где h – зазор между рабочими поверхностями; S₁₁ – площадь контакта образца и рабочей поверхности; F – приложенная сила; V_отн – относительная скорость движения пластин.

Определение значений _эф концентрированных растворов и расплавов полимеров различными методами в изотермических условиях приводит к аналогичным результатам, если выбраны идентичные области  и .

3.3. Термомеханический метод изучения физических состояний пленкообразователей

При достаточно большой длине макромолекулы, независимо от степени заторможенности вращения отдельных групп атомов в повторяющемся звене, можно выделить ее участок, концы которого способны перемещаться независимо друг от друга. При этом, если макромолекула является гибкой (т. е. звенья в ней перемещаются относительно свободно), данный участок будет по размерам меньше, чем в случае жесткой макромолекулы, в которой вращение отдельных групп существенно заторможено.

Наглядно это можно продемонстрировать на следующем опыте. Разместим на плоскости произвольно изогнутую нить и рядом жесткую проволоку, изогнутую точно так же (см. рис. 18). Затем сдвинем нить в определенном месте на некоторую величину . При этом какой-то участок нити, расположенный вблизи точки сдвига, также сместится, но он будет небольшой, поскольку нить гибкая. То же проделаем с жесткой проволокой и убедимся, что, сместив отдельную ее точку на ту же величину , мы изменим ее положение почти полностью. Отмеченные на рис. 18 пунктиром кривые и являются тем участком макромолекулы, концы которого перемещаются независимо друг от друга.



1



2

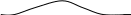
3

Рис. 18. Демонстрация гибкост

и и жесткости макромолекул: