
20. Производная сложной функции.
⊐ u
=f
(x1,
x2,
…, xm)
– сложная функция, где x1
=
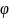 (t1,
t2,
…, tk),
x2
=
(x1,
t2,
…, tk),
…, xm
=
(x1,
t2,
…, tk)
(t1,
t2,
…, tk),
x2
=
(x1,
t2,
…, tk),
…, xm
=
(x1,
t2,
…, tk)
Теорема
⊐ функции
x1
=
(t1,
t2,
…, tk),
x2
=
(t1,
t2,
…, tk),
…, xm
=
(t1,
t2,
…, tk)
дифференцируемы в некоторой точке M
(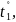
 ,
…,
,
…,
 ),
а функция u
= f
(x1,
x2,
…, xm)
дифференцируема в соответствующей
точке N
(
),
а функция u
= f
(x1,
x2,
…, xm)
дифференцируема в соответствующей
точке N
(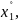
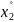 ,
…,
,
…, ),
где
),
где
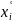 =
i(
,
…,
),
i
= 1, 2, …, m.
Тогда сложная функция u
= =
f
(x1,
x2,
…, xm),
где x1,
x2,
…, xm
определяются соотношениями x1
=
(t1,
t2,
…, tk),
x2
=
(t1,
t2,
…, tk),
…, xm
=
(t1,
t2,
…, tk),
дифференцируема в точке M
определяются формулами
=
i(
,
…,
),
i
= 1, 2, …, m.
Тогда сложная функция u
= =
f
(x1,
x2,
…, xm),
где x1,
x2,
…, xm
определяются соотношениями x1
=
(t1,
t2,
…, tk),
x2
=
(t1,
t2,
…, tk),
…, xm
=
(t1,
t2,
…, tk),
дифференцируема в точке M
определяются формулами
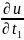 =
=
 +
+
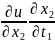 + … +
+ … +
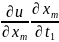 ,
,
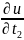 =
=
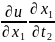 +
+
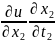 + … +
+ … +
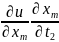 ,
……………………………………….
,
……………………………………….
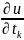 =
=
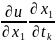 +
+
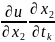 + … +
+ … +
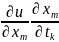 ,
,
в
которых все частные производные
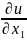 ,
,
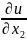 ,
…,
,
…,
 берутся в точке N,
а все частные производные
берутся в точке N,
а все частные производные
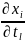 функции u
=f
(x1,
x2,
…, xm),
где x1
=
(t1,
t2,
…, tk),
x2
=
(t1,
t2,
…, tk),
…, xm
=
(t1,
t2,
…, tk),
по аргументам t1,
t2,
…, tk
берутся в
точке M.
функции u
=f
(x1,
x2,
…, xm),
где x1
=
(t1,
t2,
…, tk),
x2
=
(t1,
t2,
…, tk),
…, xm
=
(t1,
t2,
…, tk),
по аргументам t1,
t2,
…, tk
берутся в
точке M.
Доказательство
Придадим аргументам t1, t2, …, tk в точке
M ( , …, ) произвольные приращения
t1, t2, …, tk, не равные одновременно нулю. Этим приращениям соответствуют приращения x1, x2, …, xm функций x1 = (t1, t2, …, tk), x2 = (t1, t2, …, tk), …, xm = = (t1, t2, …, tk) в точке M. Приращениям x1, x2, …, xm в свою очередь соответствует приращение u функции u = f (x1, x2, …, xm) в точке N. Поскольку функция u = f (x1, x2, …, xm) предполагается дифференцируемой в точке N, указанное приращение u этой функции может быть записано в виде
u
=
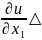 x1
+
x1
+
 x2
+
… +
x2
+
… +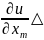 xm
+
1
x1+
+
2
x2
+ … +
m
xm,
где частные производные
xm
+
1
x1+
+
2
x2
+ … +
m
xm,
где частные производные
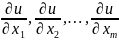 берутся в точке N,
а
1,
2,
…,
m
– бесконечно малые при
берутся в точке N,
а
1,
2,
…,
m
– бесконечно малые при
x1→0, x2→0, …, xm→0 функции, равные нулю при x1 = x2 = … = xm = 0. Подчеркнём, что в соотношении u = x1 + x2 + … + xm + 1 x1+ + 2 x2 + … + m xm, x1, x2, …, xm представляют собой приращения функций x1= (t1, t2, …, tk), x2 = (t1, t2, …, tk), …, xm = (t1, t2, …, tk), отвечающие выбранным приращениям t1, t2, …, tk аргументов этих функций. В силу дифференцируемости функций x1= (t1, t2, …, tk), x2 = (t1, t2, …, tk), …, xm = (t1, t2, …, tk) в точке M ( , …, ) указанные приращения xi, можно записать в следующей форме:
xi
=
 t1
+
t1
+
 t2
+ … +
t2
+ … +
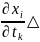 tk
+ o(
),
i
= = 1, 2, …, m,
где частные производные
tk
+ o(
),
i
= = 1, 2, …, m,
где частные производные
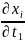 ,
,
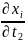 ,
…,
,
…,
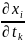 ,берутся в точке M,
а
,берутся в точке M,
а
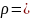 =
=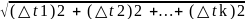
Мы
должны убедиться в том, что после
подстановки в правую часть
u
=
x1
+
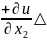 x2
+ … +
xm
+
1
x1+
+
2
x2
+ … +
m
xm
выражений
xi
=
t1
+
t2
+ … +
tk
+ o(
),
i
= = 1, 2, …, m,
приращение
u
может быть приведено к виду
x2
+ … +
xm
+
1
x1+
+
2
x2
+ … +
m
xm
выражений
xi
=
t1
+
t2
+ … +
tk
+ o(
),
i
= = 1, 2, …, m,
приращение
u
может быть приведено к виду
u
= A1
t1
+ A2
t2
+
… + Ak
tk
+ o(
),
где
Ai
=
+
+ … +
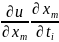 ,
i = 1, 2, …, k.
,
i = 1, 2, …, k.
Т.к. u = A1 t1 + A2 t2 + … + Ak tk + o( ) устанавливает факт дифференцируемости сложной функции, а выражение Ai = + + … + , i = 1, 2, …, k представляет собой частную производную указанной сложной функции, то доказательство теоремы будет завершено.
гд
