
Теоретические вопросы (А)
Расстояние в пространстве Rn. Свойства расстояния
Расстоянием между двумя точками P = (x1,…,xn) и P` = (x`1,…,x`n) в пространстве Rn называется число
ρ(P,P`)=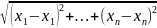 .
Последовательность точек {Pk}в
Rn
сходится к точке P0,
если соответствующая последовательность
расстояний от Pk
до P0
стремится к нулю, то есть limk→∞
.
Последовательность точек {Pk}в
Rn
сходится к точке P0,
если соответствующая последовательность
расстояний от Pk
до P0
стремится к нулю, то есть limk→∞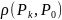 =0.
При этом P0
называют
пределом последовательности {Pk},
используя обозначения limk→∞
Pk=
P0
или Pk→P0
=0.
При этом P0
называют
пределом последовательности {Pk},
используя обозначения limk→∞
Pk=
P0
или Pk→P0
Свойства расстояния:
ρ(x,x1)≥0
ρ(x,x1)=0 ↔ x=x1
ρ(x,x1)= ρ(x1,x) ∀ x,x1 ∊ Rn
ρ(x,x1)+ ρ(x1,x2) ≥ ρ(x,x2)
| x,x1|+| x1,x2| ≥ |x,x2|
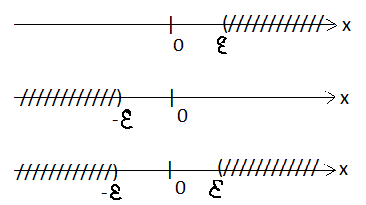
2. Окрестность точки в Rn.
 a,
a,
 n,
n,
Множество
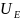 (a)
= (a
̶
(a)
= (a
̶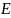 ,
a
+
)
= {x
,
a
+
)
= {x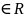 n:
|x-a|<
} –
-окрестность
точки a.
n:
|x-a|<
} –
-окрестность
точки a.

Множество
 (a)
= (a
̶
,
a)
(a)
= (a
̶
,
a)
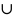 (a,
a
+
)
= {x
(a,
a
+
)
= {x }
– проколотая окрестность точки a.
}
– проколотая окрестность точки a.
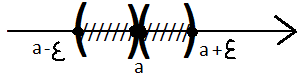
-(a)
=(a ̶
,
a) = {x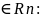 a –
a –
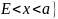 – левая
…
– левая
…
+(a)
= (a,
a
+
)
= {x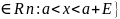 - и правая
-
- и правая
- точки a.
точки a.
(+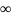 )
= (
)
= ( )
= {x
)
= {x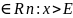 }
}
(-
)
= (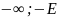 )
= {x
)
= {x }
}
(
)
= (
)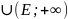
Внутренние и граничные точки множества.
Точку P0 ∊ Rn называют внутренней точкой множества D ⊂ Rn, если найдется такой шар Br(P0), r > 0, с центром в P0, который целиком содержится в D. Точку P0 ∊ Rn называют граничной точкой множества D ⊂ Rn, если каждый шар Br(P0), r > 0, с центром в P0 содержит как точки множества D, так и точки, не принадлежащие множеству D. Если множество D ⊂ Rn имеет размерность n, то множество его граничных точек называется границей множества D.
Открытые и замкнутые множества
Пусть D ⊂ Rn; Rn\D – дополнение множества D до Rn. Множество D ⊂ Rn называется открытым, если все его точки – внутренние (или если множество задано системой только строгих неравенств). Множество D – замкнутое, если его дополнение в Rn открыто ( или если D задано системой, состоящих из уравнений и/или нестрогих неравенств).
Изолированные и предельные точки множества.
Пусть D – произвольное множество в Rn. Точку P0∊ Rn называют предельной точкой множества D, если найдется такая последовательность точек {Pk} множества D, отличных от P0, что limk→∞Pk= P0. Точки множества D, не являющиеся предельными, называют его изолированными точками. Множество, содержащее все свои предельные точки, называют замкнутым.
6. Ограниченные множества.
Множество
D⊂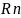 называют
ограниченным, если оно целиком содержится
в некотором шре. Множество D⊂
ограничено
тогда и только тогда, когда найдётся
такое R>0,
что D⊂
называют
ограниченным, если оно целиком содержится
в некотором шре. Множество D⊂
ограничено
тогда и только тогда, когда найдётся
такое R>0,
что D⊂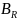 (O),
где O
– начало координат.
(O),
где O
– начало координат.
7. Сходимость последовательности точек в Rn, её эквивалентность покоординатной сходимости.
⊐ {Xk} – последовательность точек в .
{Xk}
сходится к точке X0,
если числовая последовательность { }
} 0
при k
0
при k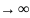 ,
т.е.
,
т.е. =
=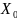 .
Можно сформулировать эквивалентное
определение сходимости последовательности
точек в
.
.
Можно сформулировать эквивалентное
определение сходимости последовательности
точек в
.
⊐
=
(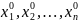 ),
),
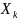 =
(
=
( )k,
)k,
…,
)k),
k∈ℕ
)k,
)k,
…,
)k),
k∈ℕ
Тогда {Xk} X ⟺последовательность соотв. координат и последовательность последних координат:

{Xk} называется фундаментальной, если
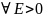
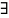 n0
(
)
n0
(
)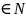 |
|
 k
k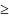 n0,
p
n0,
p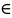 ℕ
ℕ
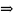
 (
(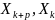 )
<
.
Для того,
чтобы последовательность {Xk}
пр-ва
была
сходящейся, необходимо и достаточно,
чтобы она была фундаментальной.
)
<
.
Для того,
чтобы последовательность {Xk}
пр-ва
была
сходящейся, необходимо и достаточно,
чтобы она была фундаментальной.
