3. Графическая часть расчета кинематической схемы коробок передач
При проектировании кинематической схемы коробок передач применяют аналитический и графо-аналитический методы. Последний метод предпочтительнее вследствие наглядности, удобства варьирования и уменьшения вероятности ошибок. При графо-аналитическом методе аналитически определяют диапазон регулирования частот вращения Rn число ступеней скорости z и число зубьев колес в передачах
Графическая часть метода состоит в построении структурной сетки и графика (картины) частот вращения с целью определения передаточных величин.
Построение ведут на базе логарифмической шкалы. Логарифмируя выражение nz = n1z-1, связывающее максимальную nz и минимальную n1 частоты вращения, получим:
lgnz = lg n1 + (z-1) lg. (3.1)
Каждое деление шкалы (рис. 3.1) соответствует логарифму определенной частоты вращения, но около деления пишется значение этой частоты (или номер ступени скорости). Шкала разделена на z-1 интервалов, каждый из которых равен lg .
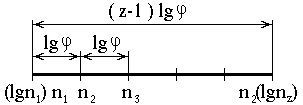
Рис. 3.1. Логарифмическая шкалa,
частот вращения
Таблица 3.1.
Характеристика групп
Названия групп в кинематическом порядке |
Число передач в группе |
Характеристика х группы |
Основная 1-я переборная 2-я переборная ......................... (k-1)-я переборная k-я переборная |
p0 p1 p2 ............... pk-1 pk |
1 p0 p0p1 ................... p0p1p2...pk-2 p0p1p2...pk-1 |
В коробке передач по рис. 3.4 p1 = 4 - основная группа, а p2 = 3 - первая переборная.
Кинематический порядок групп может не совпадать с порядком их конструктивного расположения. Оба порядка учитывают при составлении формулы структуры привода, которая для примера на рис. 3.4 записывается так: z = 12 = 41 · 32.
Каждый сомножитель означает число передач, составляющих группу. Порядок расположения сомножителей соответствует порядку расположения групп передач от двигателя к выходному валу (к шпинделю). Индексы у сомножителей показывают кинематический порядок.
3.1. Выбор структуры и построение структурных сеток.
При разработке кинематической схемы коробки передач, вычислив z, составляют формулу структуры, далее строят структурную сетку, а затем график частот вращения. Каждый шаг должен рассматриваться в вариантах, из которых один выбирают для проработки на последующем этапе.
Представим число ступеней z = 12 в виде произведения трех сомножителей: 2·2·3. Это означает, что должно быть три группы передач, порядок расположения и кинематический порядок которых следует выбрать.
Каждой выбранной формуле структуры однозначно соответствует структурная сетка, которая отличается от графика частот вращения прежде всего полной и обязательной симметричностью (в графике лишь некоторые лучи симметричны, причем это необязательно). Постоянные (одиночные) передачи в сетке не отражаются.
Пусть, например, выбрана структура z = 12 = 22 · 33 · 21. Для структурной сетки сначала проводят линии, соответствующие валам- на одну больше, чем число сомножителей в формуле структуры (число групп передач). Перпендикулярно проводят z линий по числу ступеней скорости (рис. 3.2). Сбоку пишут число передач p и характеристику х для каждой группы (индексы у р и х показывают номер группы в конструктивном порядке расположения). В данном случае за основную группу принята группа с двойным блоком, расположенная в конце.
Построение структурной сетки начинают с точки 0 (рис. 3.2,а). Из каждой выделенной точки проводят симметрично столько лучей, сколько существует передач в данной группе, т.е. р, причем число интервалов шкалы между концами смежных лучей равно характеристике данной группы.
Структурная сетка не показывает частоты вращения и передаточные величины. Она отражает лишь соотношение между передаточными величинами в каждой группе, которое выражено уравнением (3.3). Характеристика каждой группы, а следовательно, число интервалов (lg) между концами соседних лучей одинаковы в сетке и графике.
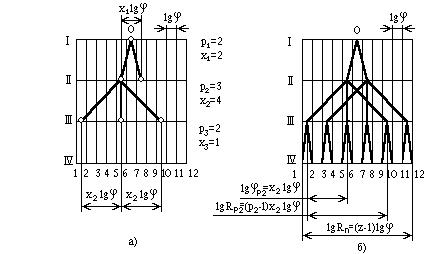
Рис. 3.2. Построение структурной сетки для z = 12 = 22 · 34 · 21:
а - начало построения; б - полная сетка
Структура z = 12 = 23 · 31 · 22 отличается от предыдущей только кинематическим порядком. Здесь основная группа находится в середине. Характеристики: х1 = 6, х2 = 1, х3 = 3.
В структуре z = 12 = 31 · 22 · 23 (рис. 3.3) другой порядок расположения групп. Тройная передача оказалась в начале, но осталась основной. Характеристики: х1 =1, х2 =3, х3 =6.
Общее число вариантов структур зависит от возможного числа перестановок в конструктивном и кинематическом порядках:
(К!)2/q! ,
где К - общее число групп передач; q - число групп с равными числами передач.
При сравнении вариантов структурных сеток необходимо обращать внимание на размах крайних лучей, выходящих из одной точки (в каждой группе). Число интервалов lg между концами таких лучейопределяет диапазон регулирования Rp в группе (характеристику группы) (см. рис. 3.2, б).
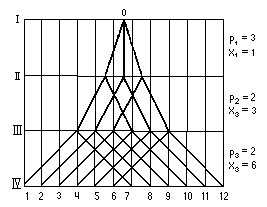
Рис. 3.3. Структурная сетка для z = 12 = 31 · 22 · 23 .