
- •Емтихан сұрақтары
- •Анықталған интеграл және оның қасиеттері
- •Риман интегралы геометриялық және механикалық есептерде қолданылуы
- •Көп айнымалы функция, оның шегі, үзіліссіздігі
- •Шартты экстремум. Мысал
- •Сандық қатарлар және оның қасиеттері. Геометриялық прогрессия қатары
- •Функционалдық қатар. Дәрежелік қатардың жинақтылығы. Абель теоремасы
- •Екі еселі интегралды есептеу, айнымалыны алмастыру. Екі еселі интегралды полярлы жүйеде есептеу
- •Үш еселі интегралды қайталама интегралдау арқылы есептеу
- •Үш еселі интегралды геометриялық және механикалық есептерді шешуге қолдануы
Шартты экстремум. Мысал
Анықтама
1.
f
(x,
y)
функциясының шартты экстремумы деп
оның аргументтері φ
(x,
y)
=
0
теңдеуімен ( байланыс теңдеуі) байланысты
шартпен берілгендегі табылған осы
функцияның максимумы немесе минимумын
айтамыз. f
(x,
y)
функциясының
φ
(x,
y)
=
0
қатысы орындалғандағы шартты экстремумын
табу үшін Лагранж функциясын құрамыз:
F(x,
y)
=
f
(x,
y)
+
λφ
(x,
y),
мұндағы λ
-
анықталмаған тұрақты көбейткіш(Лагранж
көбейткiшi),
жəне осы көмекші функцияның кəдімгі
экстремумын табамыз. Экстремумның
қажетті шарттары мынадай теңдеулер
жүйесіне əкеледі: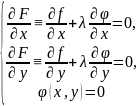 үш
x,
y, λ
белгісізі
бар жəне оны анықтауға болады.
Осы
шарттардан
үш
x,
y, λ
белгісізі
бар жəне оны анықтауға болады.
Осы
шарттардан
 - табылады. Мұндағы
- табылады. Мұндағы
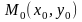 - стационар нүкте, яғни бұл нүктеде
шартты экстремум бар болуы мүмкiн.
Шартты экстремумның табылуы мен
мінездемесі туралы сұрақ Лагранж
функциясының екінші дифференциалының
таңбасын анықтау негізінде шешіледі:
- стационар нүкте, яғни бұл нүктеде
шартты экстремум бар болуы мүмкiн.
Шартты экстремумның табылуы мен
мінездемесі туралы сұрақ Лагранж
функциясының екінші дифференциалының
таңбасын анықтау негізінде шешіледі:
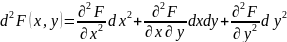 жүйедегі
x, y, λ
мəндері,
(2)-ден алынған dx
жəне
dy
төмендегі
қатынастармен байланысты болатындай:
жүйедегі
x, y, λ
мəндері,
(2)-ден алынған dx
жəне
dy
төмендегі
қатынастармен байланысты болатындай:
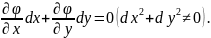 f
(x,
y)
функциясының шартты максимумы бар, егер
d2F
<
0
жəне шартты минимумы бар, егер d2F
>
0
болса. Дербес жағдайда, егер F(x,
y)
функциясының стационар нүктесіндегі
дискриминанты Δ
оң
болса, онда бұл нүктеде f
(x,
y)
функциясының шартты максимумы бар
болады, егер А<0 (немесе С<0) болса жəне
шартты минимумы бар болады, егер А>0
(немесе С>0) болса. Үш жəне одан да көп
айнымалы функциялардың экстремумдары
да дəл осылай табылады (байланыс теңдеулер
саны айнымалылар санынан аз болуы
керек). Бұнда Лагранж функциясына
байланыс теңдеуінде қанша анықталмаған
көбейткіштер болса, сонша анықталмаған
көбейткіш енгіземіз. Мысал.
f
(x,
y)
функциясының шартты максимумы бар, егер
d2F
<
0
жəне шартты минимумы бар, егер d2F
>
0
болса. Дербес жағдайда, егер F(x,
y)
функциясының стационар нүктесіндегі
дискриминанты Δ
оң
болса, онда бұл нүктеде f
(x,
y)
функциясының шартты максимумы бар
болады, егер А<0 (немесе С<0) болса жəне
шартты минимумы бар болады, егер А>0
(немесе С>0) болса. Үш жəне одан да көп
айнымалы функциялардың экстремумдары
да дəл осылай табылады (байланыс теңдеулер
саны айнымалылар санынан аз болуы
керек). Бұнда Лагранж функциясына
байланыс теңдеуінде қанша анықталмаған
көбейткіштер болса, сонша анықталмаған
көбейткіш енгіземіз. Мысал.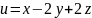 үшін
үшін
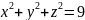
Шешімі:
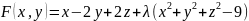
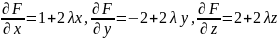
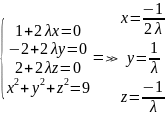
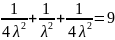
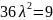
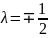
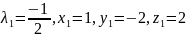
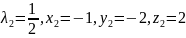
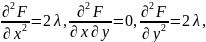
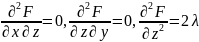
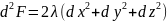
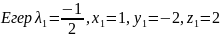 онда
онда
 .
Осы
нүкте функцияның шартты максимум
нүктесі болады.
.
Осы
нүкте функцияның шартты максимум
нүктесі болады.
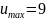
 онда
онда
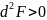 .
Осы нүкте функцияның шартты минимум
нүктесі болады.
.
Осы нүкте функцияның шартты минимум
нүктесі болады.
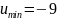 Жауабы:
Жауабы: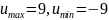
13-билет
Сандық қатарлар және оның қасиеттері. Геометриялық прогрессия қатары
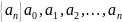
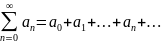

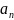 -
жалпы мүше ;
-
жалпы мүше ;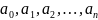 -қатар
мүшелері; Әрбір мүше- функция.
-қатар
мүшелері; Әрбір мүше- функция.
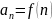
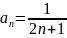 :
1+
:
1+
сандық қатар оң таңбалы болады
S1=a0;
S2=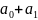 ;
S3=
;
S3=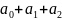 ;
Sn=
;
Sn=
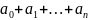
Sn-дербес қосындылардың тізбегі.
S=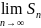 S=
S=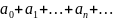 S-қатар
қосындысы.
S-қатар
қосындысы.
Егер S қосындысы бар болса, онда қатар жинақты. Егер S қосындысы жоқ немесе шексіздікке тең болса, онда қатар жинақсыз.
0
 +0+...+0
–жинақты (шегі бар)
+0+...+0
–жинақты (шегі бар)1+1+...+1+... –жинақсыз
1-1+1-1+1...-жинақсыз (шегі жоқ)
Сандық қатардың қасиеттері:
Егер қатары жинақты болса, және с
 тұрақты сан болса, онда
тұрақты сан болса, онда
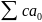 да жинақсыз.
да жинақсыз.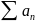 және
және
 қатарлары
қатарлары
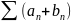 және
осы қатарлар айырымы
және
осы қатарлар айырымы
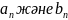 жинақты болса, жинақты.
жинақты болса, жинақты.жинақсыз болса, жинақты немесе жинақсыз болады.
an+1+ an+2+…+an+3+… Егер қатар жинақты болса, онда қалдық қатар да жинақты.
 қалдық
S=Sn+Zn
Zn-
қалдық қатар.
қалдық
S=Sn+Zn
Zn-
қалдық қатар.
Геометриялық прогрессия.
a+aq+aq2+…+aqn-1+… эталондық қатар
S= ,
n
,
n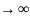
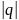 -
еселік
-
еселік
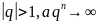 жинақсыз
жинақсыз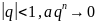 жинақты
жинақты
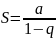
q= 1 –жинақсыз
Мысал:
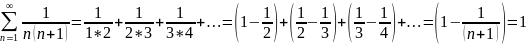
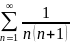 -
жинақты.
-
жинақты.
14-билет
Сандық қатар жинақтылығының қажетті шарты. Гармоникалық қатар
Th-1:
егер

Дәлелдеу:
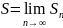 ,
,
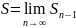 .
.
 .
.
Мысал:
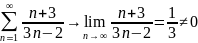 .
.
 2-ші
эталондық қатар немесе гармоникалық
қатар.
2-ші
эталондық қатар немесе гармоникалық
қатар.
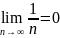
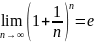
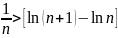
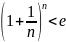
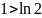
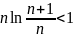
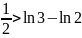
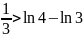
- - - - - - - - - - - - - - - - - -
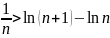
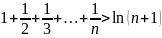
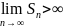
15-билет
Таңбалары тұрақты сандық қатардың жинақтылық заңдарының жеткілікті шарттары (Салыстыру, Даламбер, Коши радикалы)
Салыстыру:
Теорема(салыстыру белгісі):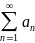 (5)
(5)
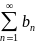 (6) an
(6) an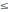 bn
(7)
bn
(7)
Егер жинақты болса, онда - да жинақты. жинақтылығынан қатардың жинақтылығы шығады, жинақсыздығынан жинақсыздығы шығады.
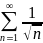
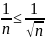 жинақсыз
жинақсыз
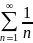
Теорема:(салыстырудың
шектік белгісі): Егер
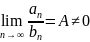 Онда
және
қатарлар бір мезгілде жинақтыб бір
мезгілде жинақсыз.
Онда
және
қатарлар бір мезгілде жинақтыб бір
мезгілде жинақсыз.
Мысал:
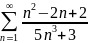
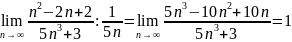
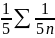 жинақсыз.
жинақсыз.
Доламбер
белгісі:
;
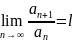
 жинақты;
жинақты;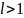 жинақсыз;
жинақсыз;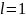 .
.
М
ысалы:
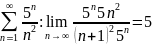
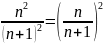 жинақсыз.
жинақсыз.
Коши
радикалы:
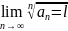
жинақты;
жинақсыз;
.
Мысалы:
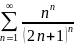
 жинақты.
жинақты.
16-билет
Кошидің интегралдық белгісі. Жалпылама гармоникалық қатар
Бізге
f(1)+f(2)+f(3)+…+f(n)+…=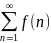 ,
бұның мүшелері қандай да бір f(x) функцияның
мәні болсын, оң үзіліссіз және [1;+
,
бұның мүшелері қандай да бір f(x) функцияның
мәні болсын, оң үзіліссіз және [1;+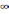 )
кемімелі болсын. Онда егер
)
кемімелі болсын. Онда егер
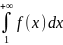 жинақталса, онда
қатары да жинақталады;
егер
жинақталса, онда
қатары да жинақталады;
егер
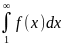 жинақталмаса, онда
қатары да жинақталмайды. Бұнда
=
жинақталмаса, онда
қатары да жинақталмайды. Бұнда
=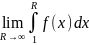
Мысал:
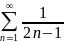 .
.
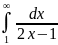 =
=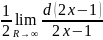 =
=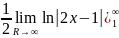 =
=
Жалпылама гармоникалық қатар.
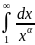 =
=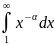 =
=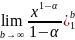 =
=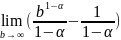
Егер
 >1
жинақты.
>1
жинақты.
Егер <1 жинақсыз.
17-билет
Таңбалары кезекпен ауыспалы сандық қатар. Лейбниц белгісі
Таңбалары
кезекпен ауыспалы сандық қатарлар деп
мына түрдегі қатарды айтамыз
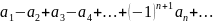 =
,
бұл жерде
>0.
=
,
бұл жерде
>0.
Бұл жерде таңбалар белгілі бір ретпен емес, кез-келген ретте ауысуы мүмкін.
Лейбниц белгісі: Егер таңбалары ауыспалы сандық қатардың мүшелері:
1)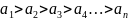 ,
яғни абсолют шамалары монотонды кемімелі
болса;
,
яғни абсолют шамалары монотонды кемімелі
болса;
2)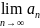 =0
болса,
онда қатар жинақталады.
=0
болса,
онда қатар жинақталады.
Мысал:
 .
.
1)
1>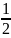 >
>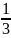 >…
монотонды
кемімелі;
>…
монотонды
кемімелі;
2)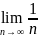 =0.
Лейбництің
екі белгісі орындалып тұр, яғни жинақты.
=0.
Лейбництің
екі белгісі орындалып тұр, яғни жинақты.
(1)қатар
абсолютті
жинақталады
болады, егер
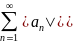 (2)
жинақталса.
Біз (1) жинақталуы туралы айтқан жоқпыз,
себебі (2) қатардың жинақталуы (1) қатардың
жинақталуына әкеледі.
(2)
жинақталса.
Біз (1) жинақталуы туралы айтқан жоқпыз,
себебі (2) қатардың жинақталуы (1) қатардың
жинақталуына әкеледі.
Мысал: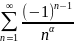 =1-
=1-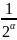 +
+ -
-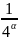 +…
, бұнда
>0.
Бұл
қатар абсолютті жинақталады, себебі
>0
+…
, бұнда
>0.
Бұл
қатар абсолютті жинақталады, себебі
>0
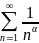 жинақталады.
жинақталады.
қатар шартты жинақталады, егер жинақты болса, ал жинақталмаса.
18-билет
