Емтихан сұрақтары

1. Анықталған интеграл және оның қасиеттері.

2. Риман интегралын есептеу әдістері. Ньютон-Лейбниц формуласы.

3. Риман интегралын геометриялық және механикалық есептеулерде қолданылуы.

4. Көп айнымалы функция,оның шегі,үзіліссіздігі.

5. Көп айнымалы функцияның дербес туындылары.Жоғарғы ретті дербес туынды.Шварц теоремасы.

6. Көп айнымалы функцияның дифференциялдануы.Толық дифференциял және оны жуықтап есептеуде қолдану.

7. Толық дифференциял формасының түрін сақтау қасиеті.

8. Көп айнымалы күрделі функцияны дифференциялдау. Толық туынды формуласы. Мысалдар.

9. Айқындалмаған функцияның бар болуы және оның дифференциялдану туралы теоремасы.

10. Кез келген бағыт бойынша туынды және Градиент.

11. Екі айнымалы функция үшін локальдық экстремумның қажетті және жеткілікті шарттары.

12. Шартты экстремум. Мысал.

13. Сандық қатарлар және оның қасиеттері.Геометриялық прогрессия қатары.

14. Сандық қатар жинақтылығының қажетті шарты. Гармоникалық қатар.

15. Таңбалары тұрақты сандық қатардың жинақтылық заңдарының жеткілікті шарттары (Салыстыру, Даламбер, Кошидің радикалдық белгісі)

16. Кошидің интегралдық белгісі. Жалпылама гармоникалық қатар.

17. Таңбалары кезекпен ауыспалы сандық қатар. Лейбниц белгісі.

18. Функционалдық қатар. Дәрежелік қатардың жинақтылығы.Абель теоремасы.

19. Дәрежелік қатардың жинақтық интервалы және жинақтылық радиусы.

20. Тейлор және Маклорен қатарлары.Тейлор қатарына жіктелудің қажетті және жеткілікті шарты.

21. Кейбір элементар функцияның Тейлор қатарына жіктелуі.

22. Екі еселі интеграл. Негізгі қасиеттері.

23. Екі еселі интегралды есептеу, айнымалыны алмастыру. Екі еселі интегралды полярлы жүйеде есептеу.

24. Екі еселі интегралдың геометриялық және механикалық есептеулерде қолданылуы.

25. Үш еселі интеграл және оның қасиеттері.

26. Үш еселі интегралды қайталама интегралдау арқылы есептеу.

27. Үш еселі интегралда айнымалыны ауыстыру.Жалпы жағдай.

28. Үш еселі интегралды цилиндрлік және сфералық координаталар жүйесінде есептеу.Мысал келтіру.

29. Үш еселі интегралды геометриялық және механикалық есептерді шешуге қолдану.

30. Дәрежелік қатардың, функцияның мәнін анықталған интегралды жуықтап есептеуге қолданылуы.

1-билет

Анықталған интеграл және оның қасиеттері

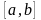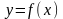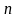Анықталған интегралдың анықтамасы. сегментінде анықталған функциясы берілсін. Осы сегментті қалауымызша алынған нүктелерімен бөлікке бөліп, әр 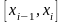бөлік сегменттен кез келген 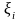нүктесін алып, Риман қосындысы немесе интегралдық қосынды деп аталатын мынадай қосынды жасайық: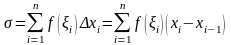 . (3)

Бұл қосындының мәні, жалпы алғанда, 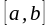сегментін бөлу тәсілінен де, нүктелеріне де тәуелді. Бөлік сегменттердің ұзындықтарының ең үлкенін 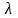, яғни 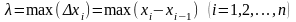деп белгілейік.

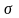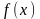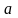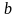Анықтама. Егер интегралдық қосынды -ның нөлге ұмтылғанда (барлық бөлік сегменттердің ұзындықтары нөлге ұмтылғанда) сегментін бөлу тәсілінен тәуелсіз және әр бөлік сегменттен нүктесін таңдап алудан тәуелсіз шекті (тиянақты) шегі бар болса, осы шекті функциясының -дан -ға дейінгі немесе сегментіндегі анықталған интегралы деп,атайды да оны 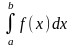деп белгілейді. 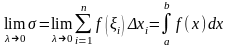. (4)

Мұндағы - интеграл астындағы функция, 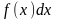- интеграл астындағы өрнек, саны –интегралдың төменгі, саны – интегралдың жоғарғы шегі, ал айнымалысы – интегралдау айнымалысы деп аталады.

Берілген анықтамадан жоғарғы, төменгі шектер тұрақты сандар болса, анықталған интеграл тұрақты санға тең болатынын байқаймыз, себебі ол айнымалы қосындының шегі.

Анықталған интегралдың негізгі қасиеттері.

1⁰.Тұрақты санды анықталған интеграл белгісінің алдына шығаруға болады: 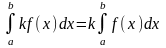, мұнда .

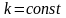Анықталған интегралдың анықтамасы бойынша

2⁰.Бірнеше функциялар қосындысының анықталған интегралы қосылғыштарының анықталған интегралдарының қосындысына тең,яғни

.

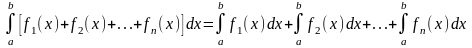Осы екі қасиет интегралдың сызықтық қасиеті д.а.

3⁰.Егер аралығын 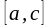және 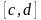аралықтарына бөлсек, онда 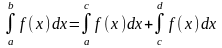Бұл аддитивтілік қасиет д.а..

4⁰.Егер интегралдың жоғарғы шегі мен төменгі шегінің орындарын ауыстырсақ, онда оның таңбасы өзгереді: .

5⁰.Жоғарғы шегі мен төменгі шегі тең болатын интеграл 0-ге тең: .

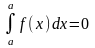6⁰.Егер аралығындағы айнымалысының барлық мәндері үшін 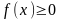болса, онда .

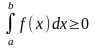7⁰.Егер аралығындағы айнымалысының барлық мәндері үшін 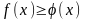болса, онда 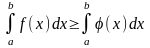. - теңсіздікті мүшелеп интегралдауға болады.

8⁰.Егер аралығындағы 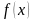функциясының ең үлкен және ең кіші мәндері сәйкес 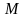мен 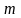сандары болса, онда . 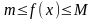қос теңсіздігін 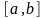кесіндісінде интегралдап 7-қасиетті пайдалансақ: 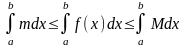немесе .

9⁰.Анықталған интегралдың орта мәні туралы теорема. Егер функциясы 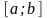сегментінде интегралданса және 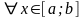үшін теңсіздіктері орындалса, оның интегралы 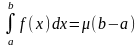( 6 ) теңдігін қанағаттандырады,мұндағы 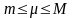теңсіздігін қанағаттандыратын тұрақты сан.

2-билет

Риман интегралын есептеу әдістері. Ньютон-Лейбниц формуласы

Риман интегралы. Анықтама. Егер интегралдық қосынды -ның нөлге ұмтылғанда (барлық бөлік сегменттердің ұзындықтары нөлге ұмтылғанда) сегментін бөлу тәсілінен тәуелсіз және әр бөлік сегменттен нүктесін таңдап алудан тәуелсіз шекті (тиянақты) шегі бар болса, осы шекті функциясының -дан -ға дейінгі немесе сегментіндегі Риман бойынша интегралданады деп,атайды да оны 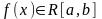деп белгілейді. санын санын Риманның анықталған интегралы д.а және д. белгілейді.

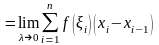
Мұндағы - интеграл астындағы функция, - интеграл астындағы өрнек, саны –интегралдың төменгі, саны – интегралдың жоғарғы шегі, ал айнымалысы – интегралдау айнымалысы деп аталады. Берілген анықтамадан жоғарғы, төменгі шектер тұрақты сандар болса, анықталған интеграл тұрақты санға тең болатынын байқаймыз, себебі ол айнымалы қосындының шегі.

Лейбниц-Ньютон формуласы. функциясы кесіндісінде интегралданатын болсын және 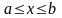. 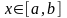үшін жаңа 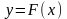функциясын былай анықтайық: .

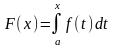Бұл жерде, 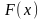жоғарғы шегі айнымалысы болатын функциясының интегралы арқылы өрнектеледі.

Теорема 2. Егер функциясы аралығында үзіліссіз болса, онда функциясы функциясының 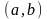аралығындағы алғашқы функциясы деп аталады,яғни, бұл аралықта .

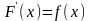Теорема. Егер 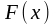функциясы 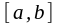аралығына 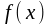функциясының алғашқы функциясы болса, онда 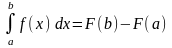. (1) Бұл теңдік Ньютон-Лейбниц формуласы деп аталады.

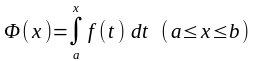
Дәлелдемесі. функциясы -да функциясының алғашқы функцияларының бірі болсын. Жоғарыда айтылған бойынша кесіндісінде функциясының алғашқы функциясы болып табылатын мына 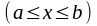функция болады. 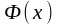пен бір ғана функциясының алғашқы функциялары болғандықтан, 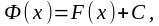яғни 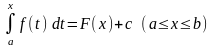. Бұдан 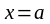болғанда 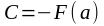теңдігі орындалады. Олай болса 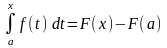. Енді 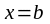деп алсақ, онда (1) формулаға келеміз.

Ньютон-Лейбниц формуласы анықталған интеграл мен алғашқы функцияның (анықталмаған интегралдың) байланысын көрсетеді. Сондықтан анықталған интегралдауды есептеуді анықталмаған интегралдарды есептеуге келтіреді, яғни бірінші теңдеуде қарастырылған анықталмаған интегралдарды есептеп шығару формулаларын пайдалануға мүмкіндік береді. Бұл формула интегралдық есептеудің негізгі формуласы деп те аталады. Ньютон-Лейбниц формуласын есептеуге ыңғайлы болу үшін, оның оң жағын 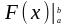символымен белгілейміз, яғни 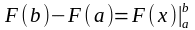. Сонда, (1) формуласы мына түрде 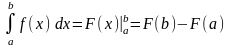жазылады. Ескертпе.Интегралды Ньютон-Лейбниц формуласы бойынша есептегенде ол формуланың қолданылуының заңдылығына әдейі көңіл бөлу керек. Бұл формуланы қолдану үшін аралығындағы үздіксіз функция -тің интегралын есептеу үшін оның алғашқы функциясы жабық кесінді -ның бүкіл бойында 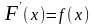теңдігін қанағаттандыру тиіс екендігі шешуші шарт екенін есте сақтау керек. Бұл талаптан функциясының кесінді бойында үздіксіз болатындығы туралы тұжырым шығады. Мысал 4. 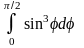тап.

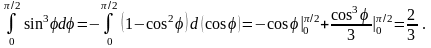
3-билет

3-билет