8.Случайные погрешности измерений

Случайные погрешности измерений изменяются при измерения случайным образом. В качестве истинного значения при многократном измерении параметра выступаетсреднеарифметическое значение которое определяется следующим образом: 

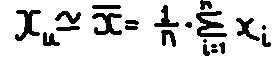
Величина Х, полученная в одной серии измерений является случайным приближением к истинному значению. Для оценки её возможных отклонений вычисляютсреднеквадратическое отклонение :

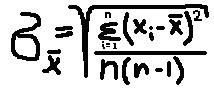
Случайные и систематические составляющие погрешности могут проявляться одновременно, поэтому общая погрешность – это их сумма :

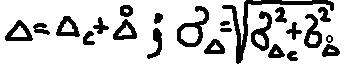
Случайные погрешности не могут быть устранены совсем, но их влияние можно уменьшить путем обработки результатов измерений. Для этого должны быть известны вероятностные и статистические характеристики, математическое ожидание, среднеквадратическое отклонение, доверительную вероятность и доверительный интервал.

>Содержание<

9.Нормирование погрешностей

Основная задача нормирования заключается в выборе показателей, характеризующих погрешность и поиске допустимых значений этих показателей.  Для оценки погрешностей измерений необходимо 

 1)Определить вид модели погрешности с её характерными свойствами.

 2)Определить характеристики этой модели.

 3)Оценить показатели точности измеренные по характеристике этой модели. При установлении модели погрешности возникают типовые статистические задачи :

 а)Оценка параметров закона распределения .

 б)Проверка гипотез.

 в)Планирование эксперимента и т.д. В соответствии с методическими указаниями точность измерения должна быть выражена одним из способов:

 а)Интервалом в котором с установленной вероятностью находится суммарная погрешность измерений.

 б)Интервалом в котором с установленной вероятностью находится систематическая составляющая погрешности измерения.

 в)Стандартной аппроксимацией функции распределения случайной составляющей погрешности и среднеквадратическим отклонением.

 г) Стандартной аппроксимацией функций распределения случайной и систематической составляющей погрешности измерения и их среднеквадратических отклонений.

>Содержание<

10.Качество измерений

Под качеством измерений понимают совокупность свойств, обуславливающих получение результата с требуемой точностью, характеристиками в необходимом виде, и в установленные сроки. Качество измерений характеризуется такими показателями как точность, правильность и достоверность .Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности.

 1)Точность: это близость результатов измерений к истинному значению измеряемой величины, если систематическая составляющая исключена, то точность результата характеризуется степенью рассеяния его значений т.е. дисперсией средней величины.

 2)Правильность: определяется близостью к нулю систематической погрешности.

 3)Достоверность: зависит от степени доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в определенных пределах. Эти вероятности называют доверительными, а границы доверительными границами. Качество измерительных операций характеризуется так же сходимостью и воспроизводимостью результатов.

 4)Сходимость: это близость результатов 2-х испытаний, полученных на идентичных установках в одной лаборатории, а воспроизводимость – это получение 2-х результатов в разных лабораториях.

>Содержание<