Экономическая интерпретация результата решения

1. Максимальная прибыль составляет 2412 тыс. руб.

За счет чего получена эта прибыль? Количество производимых изделий обозначено у нас х1, х2, х3, х4. В последней симплексной таблице х1=46, х2=30, х5=18. Тем самым в оптимальный план производства вошли 2 вида изделий из 4 возможных , это изделия В1- 46 изделий, и В3-30 изделий.

Изделия В2 и В4 по оптимальному плану производиться не вошли (поскольку их нет в списке базисных переменных в столбце П0, значит они – свободные, значит они равны 0).

Проверяем, какую прибыль должно дать производство изделий В1 и В2:

27 *46+ 39*30 = 2412 = Fmax,

как и должно быть.

2. Кроме х1 и х2 в число базисных попала и переменная х5.

Но как мы установили ранее, значение дополнительной переменной означает излишек ресурса соответствующего вида, в данном случае третьего (х5 введена в качестве дополнительной именно в третье неравенство). х5=18 означает, что ресурс первого вида (в условиях нашей задачи это сырье) при организации производства по оптимальному плану недорасходуется, остается в избытке в количестве 18 кг.

Проверяем: расход ресурса А1 на план производства составит

2*46+ 1*30 = 122,

недорасход х5=140-122=18.

Дополнительные переменные х6 и х7 в оптимальный план в качестве базисных не вошли. Это значит, что они – свободные, равны 0, и тем самым излишка ресурсов I и II вида нет, эти ресурсы (А2 и А3) по оптимальному плану в процессе производства расходуются.

Проверяем: 0*46+ 3*30 = 90,

3*46+ 2*30= 198,

действительно эти ресурсы истрачены полностью.

3. Очень полезный смысл имеют двойственные оценки.

Если отрицательная двойственная оценка показывает возможность увеличения прибыли (в расчете на 1 изделие, вводимое в план), то положительная показывает наоборот, на снижение прибыли в расчет на 1 изделие.

Занумеруем двойственные оценки по номерам столбцов, в которых они находятся: d3=18, d4= 8, d6=7 d7=9.

Изделия В3 и В4 в оптимальный план не входят. Но если включить в план одно изделие В3, то прибыль снизится на 18 тыс.руб., а В4 - на 8 тыс.руб. План перестанет быть оптимальным.

4. Ненулевые оценки имеют также столбцы Х6 и Х7:

d6=7, d7=9.

Двойственная оценка дополнительной переменной показывает, на сколько снизится прибыль при уменьшении соответствующего ресурса на 1:

при уменьшении ресурса А2 на 1 (с 90 до 89) прибыль уменьшится на 7 тыс.руб.,

при уменьшении ресурса А3 на 1 (с 198 до 197) прибыль уменьшится на 9 тыс.руб.

И наоборот, при увеличении ресурса А2 на 1 (с 90 до 91) прибыль увеличится на 7 тыс.руб.,

при увеличении ресурса А3 на 1 (с 198 до 199) прибыль увеличится на 9 тыс.руб.

Задание № 3. «Расшивка узких мест».

Решить задачу о «расшивке узких мест» для задачи оптимального планирования, решенной в п.1

Решение можно осуществить графически либо симплексным методом.

Определить новый оптимальный план, полученный в результате расшивки узких мест.

Дать экономический анализ решения.

Задача оптимального планирования выглядит так:

2 х₁+ 1х₂+ 6х₃+ 5х₄ ≤ 140

3х₂ + 4 х₄ ≤ 90

3х₁+2х₂ + 4х₃ ≤ 198

х₁≥0, х₂≥0, х₃≥0, х₄≥0

F=27х₁+ 39х₂+ 18х₃+ 20х₄ → max.

Симплексная таблица и оптимальный план этой задачи приведены в таблицах №1 и №2.

C	П	Н	27	39	18	20	0	0	0
			x1	x2	x3	x4	x5	x6	x7
0	х5	140	2	1	6	5	1	0	0
0	х6	90	0	3	0	4	0	1	0
0	х7	198	3	2	4	0	0	0	1
		0	-27	-39	-18	-20	0	0	0

Таблица №1.

Cопт	Попт	Нопт	27	39	18	20	0	0	0
			x1	x2	x3	x4	x5	x6	x7
0	х5	18	0	0	3 1/3	5 4/9	1	1/9	- 2/3
39	х2	30	0	1	0	1 1/3	0	1/3	0
27	х1	46	1	0	1 1/3	- 8/9	0	- 2/9	1/3
		2412	0	0	18	8	0	7	9

Таблица №2.

При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, т.е. образуют ²узкие места производства². Будем их заказывать дополнительно. Пусть T=(t₁,t₂,t₃)- вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие

H_опт + А₂ T , где

,

Задача состоит в том, чтобы найти вектор

T (0, t₂, t₃),

максимизирующий суммарный прирост прибыли

W = D₂T = 7t2 + 9t₃  max, где

при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)

(1)

Из неравенства (1) получаем следующую систему неравенств:

Приведём её к СЛАУ:

Решим получившуюся задачу симплексным методом. Для этого построим симплексную таблицу (таблица №3).

C	П	T	7	9	0	0	0
			t2	t3	t4	t5	t6
0	t4	18	- 1/9	2/3	1	0	0
0	t5	30	1/3	0	0	1	0
0	t6	46	2/9	- 1/3	0	0	1
		0	-7	-9	0	0	0

Таблица №3.

C	П	T	7	9	0	0	0	α	β
			t2	t3	t4	t5	t6
0	t4	18	- 1/9	2/3	1	0	0	27	1
0	t5	30	1/3	0	0	1	0	-	0
0	t6	46	2/9	- 1/3	0	0	1	-	- 1/2
		0	-7	-9	0	0	0		-13 1/2

Таблица №4.

C	П	T	7	9	0	0	0	α	β
			t2	t3	t4	t5	t6
9	t3	27	- 1/6	1	1 ½	0	0	-	- ½
0	t4	30	1/3	0	0	1	0	90	1
0	t5	55	1/6	0	½	0	1	330	½
		243	-8 ½	0	13 ½	0	0	-	-25 ½

Таблица №5.

В результате преобразований симплексного метода (таблицы №4 и №5), мы получили оптимальный план (таблица №6):

C	П	T	7	9	0	0	0
			t2	t3	t4	t5	t6
9	t3	42	0	1	1 1/2	1/2	0
7	t2	90	1	0	0	3	0
0	t5	40	0	0	1/2	- 1/2	1
		1008	0	0	13 1/2	25 1/2	0

Таблица №6.

Найденный вектор Т = (0, 90, 42).

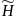_опт = Н_опт + А₂Т = (0, 60, 40),

а новая прибыль составила = F+W = 2412+1008 = 3420.

	0	60	42
	t1	t2	t3	A2T	Hст	Н’
A2	1	1/9	- 2/3	-18	18	0	x1	Fст	F’
	0	1/3	0	30	30	60	x2	2412	3420
	0	- 2/9	1/3	-6	46	40	x3