
- •Дифференциальные уравнения и ряды Сборник типовых заданий
- •1. Индивидуальные задания по дифференциальным уравнениям Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Некоторые разложения в ряд Фурье
- •Оглавление
- •1. Индивидуальные задания по дифференциальным уравнениям..........................3
- •620002, Екатеринбург, Мира, 19
- •620002, Екатеринбург, Мира, 19
Вариант 23
Пользуясь определением , найти сумму ряда
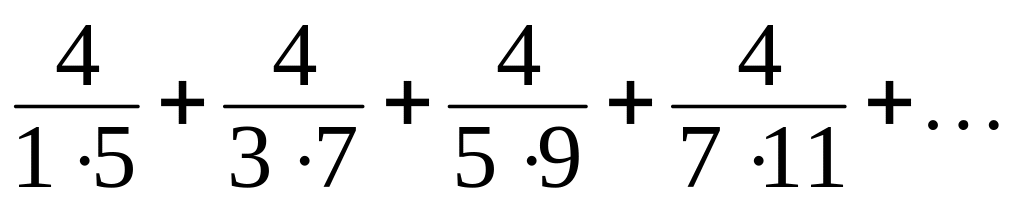
Вычислить частичные суммы ряда для .
Исследовать на сходимость и абсолютную сходимость ряды:
a)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
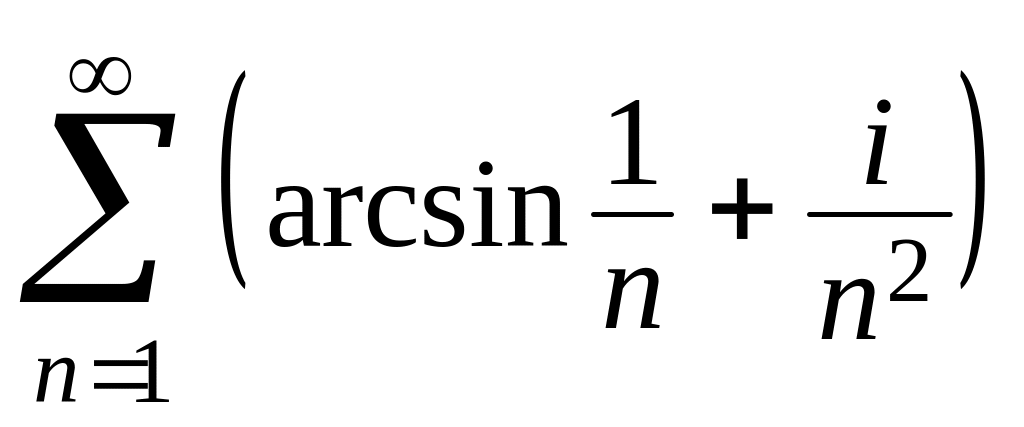 .
.
Найти область сходимости ряда
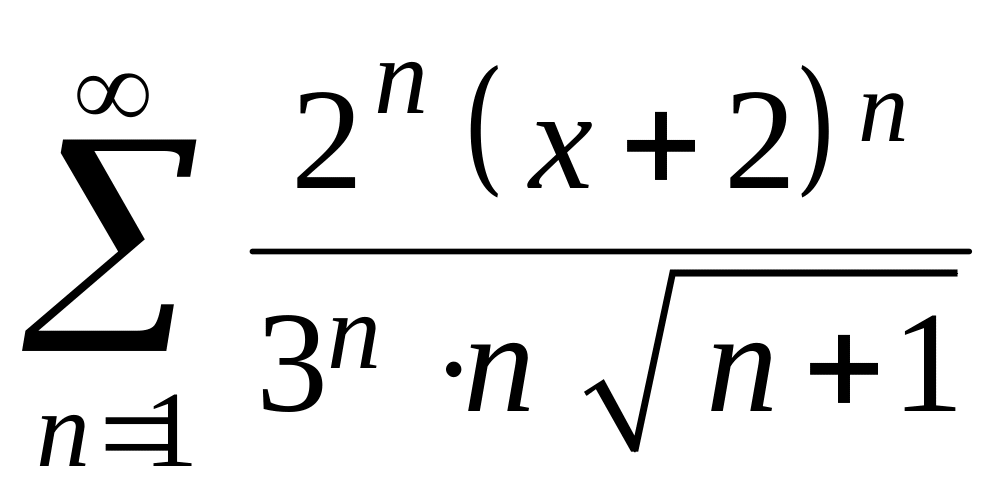 .
Вычислить с
точностью =0,01
сумму ряда в точках
,
где
– радиус сходимости ряда.
.
Вычислить с
точностью =0,01
сумму ряда в точках
,
где
– радиус сходимости ряда.Разложить функцию
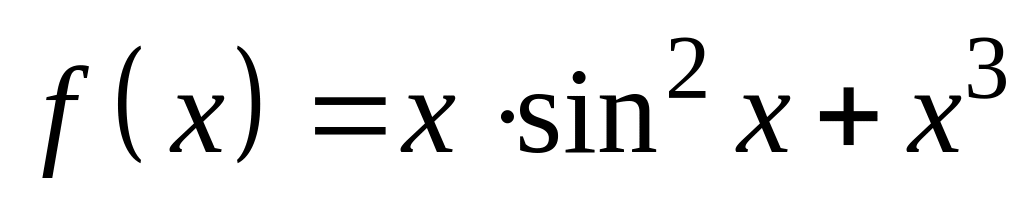 в ряд Маклорена. Определить область
сходимости полученного ряда.
в ряд Маклорена. Определить область
сходимости полученного ряда.Разложить функцию
 в ряд Тейлора по степеням
и найти область сходимости полученного
ряда.
в ряд Тейлора по степеням
и найти область сходимости полученного
ряда.Найти круг сходимости ряда
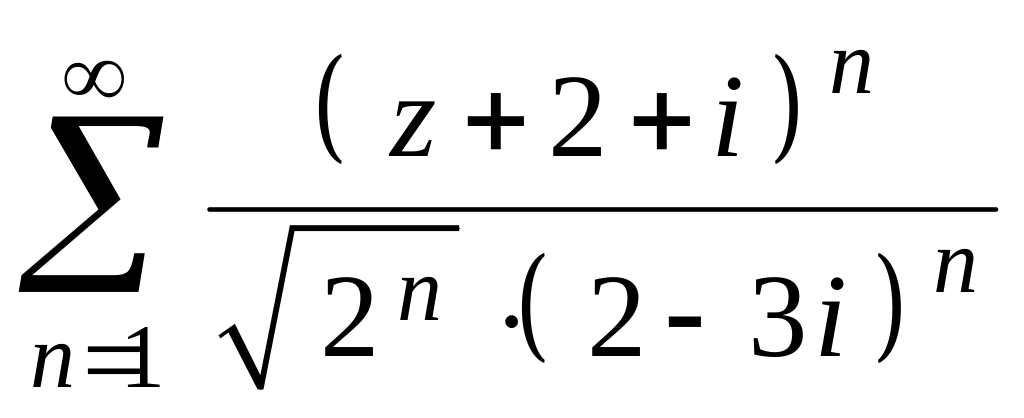 .
.Доказать, что функция
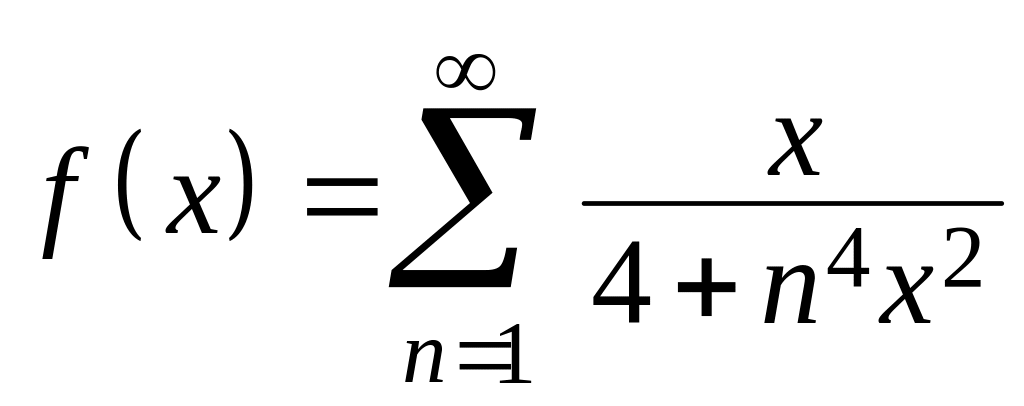 непрерывна в области определения.
непрерывна в области определения.Представить в виде степенного ряда решение дифференциального уравнения
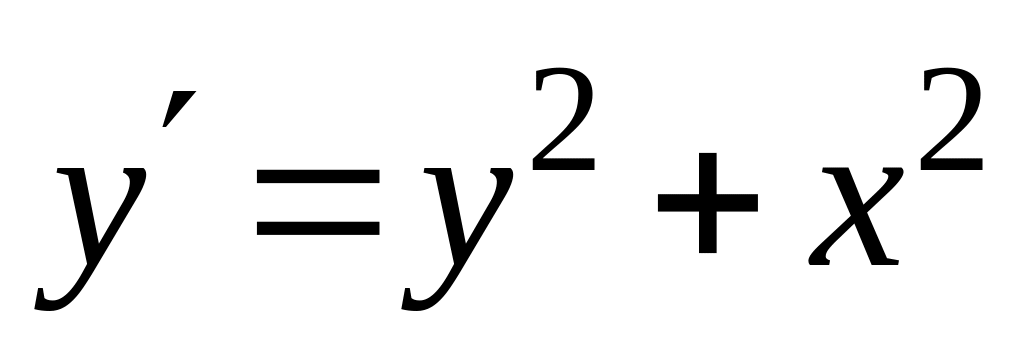 ,
удовлетворяющее начальному условию
.
Найти пять членов ряда.
,
удовлетворяющее начальному условию
.
Найти пять членов ряда.И
 спользуя
ряды, вычислить приближенное значение
интеграла
спользуя
ряды, вычислить приближенное значение
интеграла
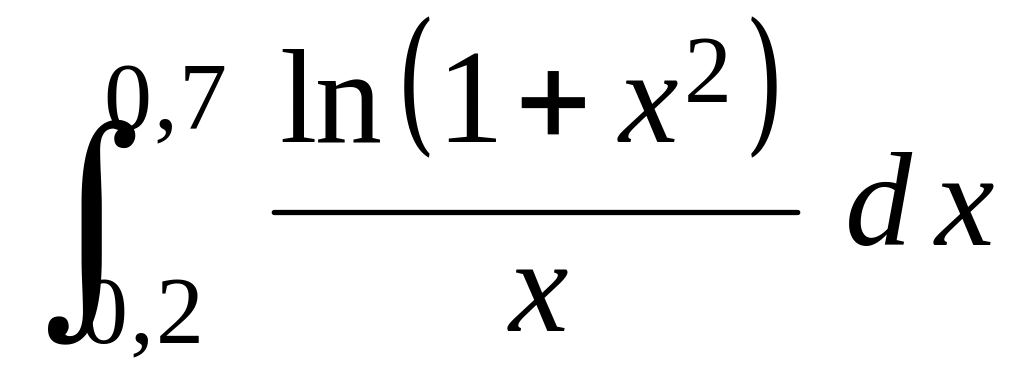 с точностью =10-3.
Указать число членов ряда, взятых в
частичную сумму для достижения нужной
точности на верхнем и нижнем пределах
интегрирования.
с точностью =10-3.
Указать число членов ряда, взятых в
частичную сумму для достижения нужной
точности на верхнем и нижнем пределах
интегрирования.
Разложить в ряд Фурье:
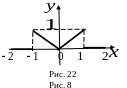
a) периодическую функцию с периодом (рис. 22),
б)
функцию
![]() ,
заданную на промежутке
,
продолжая её чётным или нечётным образом
на промежуток
.
Построить график суммы полученного
ряда.
,
заданную на промежутке
,
продолжая её чётным или нечётным образом
на промежуток
.
Построить график суммы полученного
ряда.
Пользуясь табличными разложениями функций в ряд Фурье, найти сумму числового ряда
 .
.
Вариант 24
Пользуясь определением , найти сумму ряда
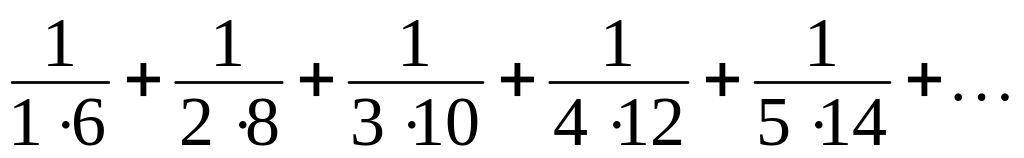
Вычислить частичные суммы ряда для .
Исследовать на сходимость и абсолютную сходимость ряды:
a)
![]() ,
б)
,
б)
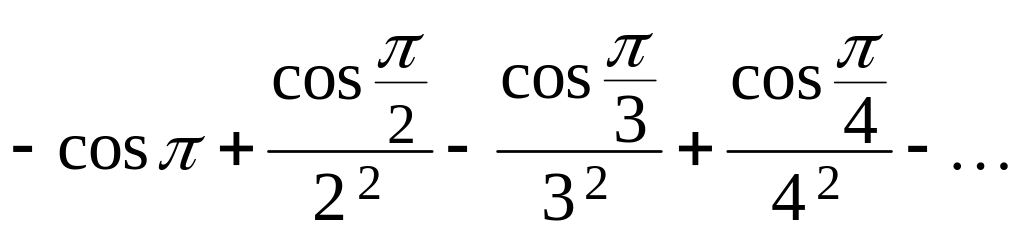 ,
в)
,
в)
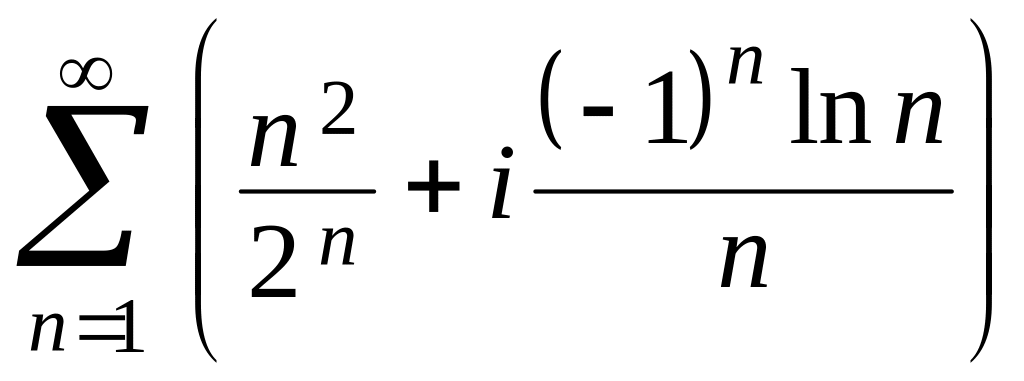 .
.
Найти область сходимости ряда
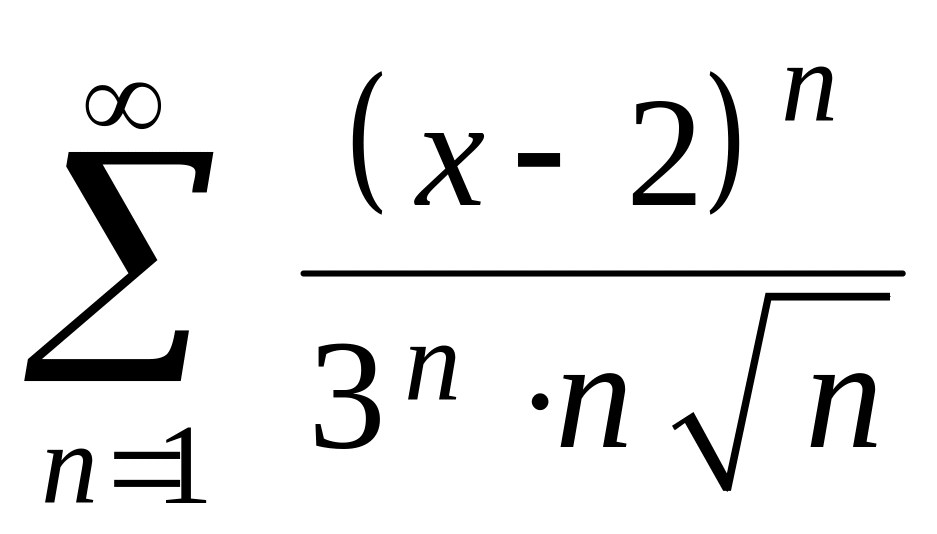 .
.
Вычислить с точностью =0,01 сумму ряда в точках , где – радиус сходимости ряда.
Разложить функцию
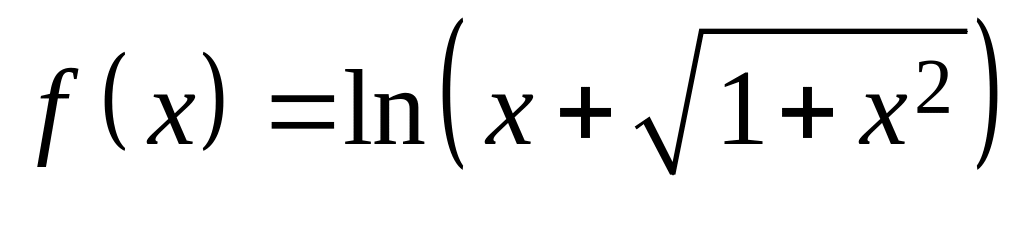 в ряд Маклорена.
Определить область сходимости полученного
ряда.
в ряд Маклорена.
Определить область сходимости полученного
ряда.Разложить функцию
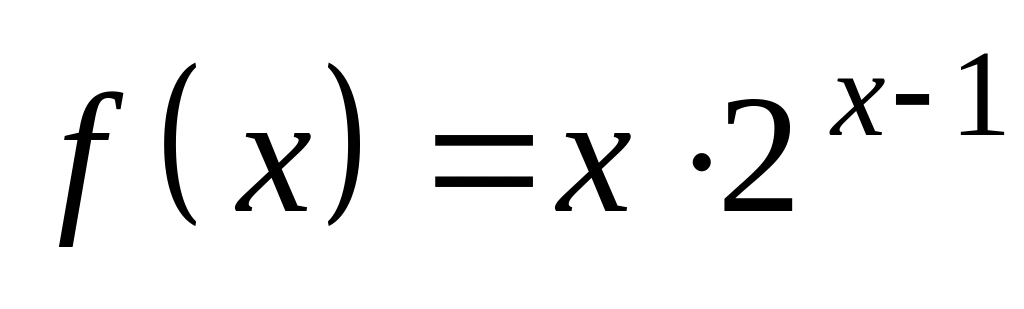 в ряд Тейлора по степеням
и найти область сходимости полученного
ряда.
в ряд Тейлора по степеням
и найти область сходимости полученного
ряда.Найти круг сходимости ряда
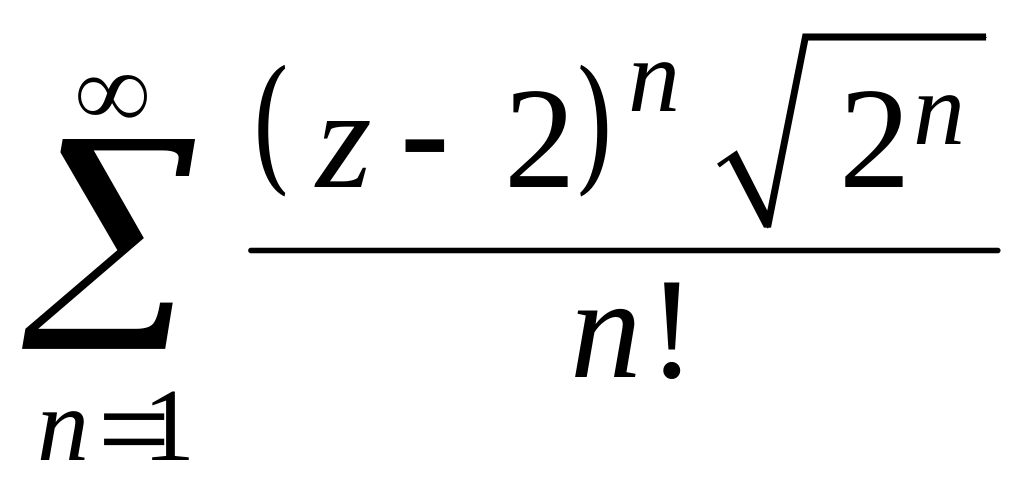 .
.Показать, что тета-функция
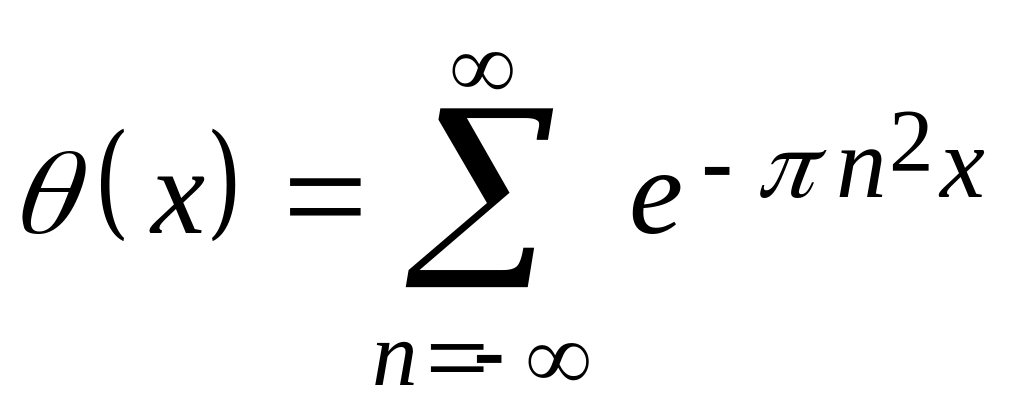 определена и
дифференцируема при
.
определена и
дифференцируема при
.
Представить в виде степенного ряда решение дифференциального уравнения
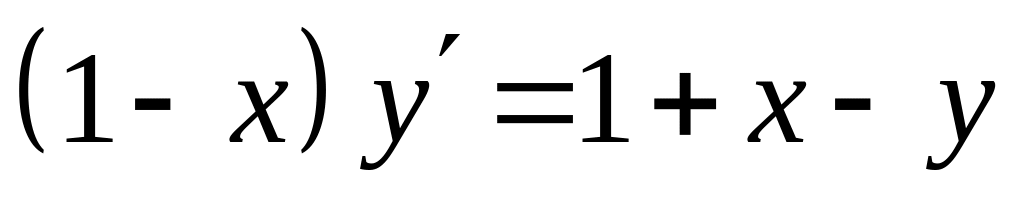 ,
удовлетворяющее начальному условию
.
Найти четыре члена ряда.
,
удовлетворяющее начальному условию
.
Найти четыре члена ряда.Используя ряды, вычислить приближенное значение интеграла
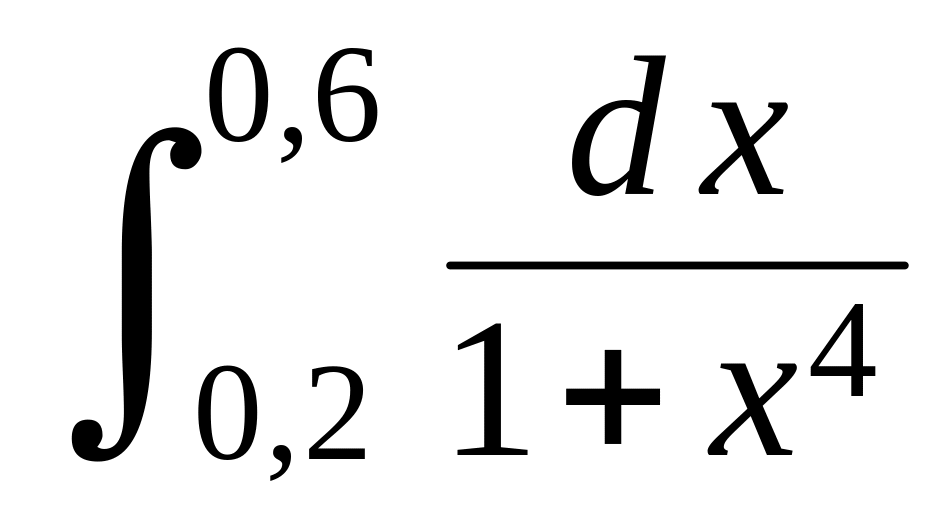
с точностью =10-3. Указать число членов ряда, взятых в частичную сумму для достижения нужной точности на верхнем и нижнем пределах интегрирования.
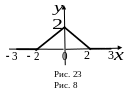 Разложить
в ряд Фурье:
Разложить
в ряд Фурье:
a)
периодическую функцию с периодом
![]() (рис. 23),
(рис. 23),
б)
функцию
![]() заданную на промежутке от
заданную на промежутке от
![]() ,
продолжая её чётным или нечётным образом
на промежуток
,
продолжая её чётным или нечётным образом
на промежуток
![]() .
Построить график суммы полученного
ряда.
.
Построить график суммы полученного
ряда.
Пользуясь табличными разложениями функций в ряд Фурье, найти сумму числового ряда
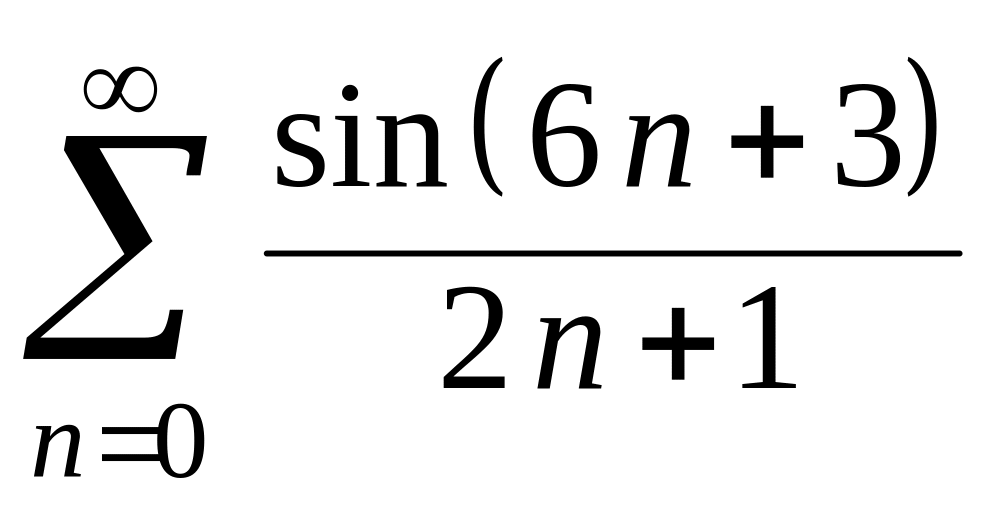 .
.
Некоторые разложения в ряд Фурье
Ниже приведены разложения в ряд Фурье некоторых простейших функций, заданных на определенных интервалах.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]() при
при
![]() и нечетно продолжена на
и нечетно продолжена на
![]() ;
;
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Оглавление
1. Индивидуальные задания по дифференциальным уравнениям..........................3
2. Индивидуальные задания по рядам.....................................................................15
3. Некоторые разложения в ряд Фурье....................................................................39
Дифференциальные уравнения и ряды
Сборник типовых заданий
Редактор Н.П. Кубыщенко
Компьютерная верстка Р.М. Миньковой, А.В.Зенкова
ИД № 06263 от 12.11. 2001 г.
Подписано в печать Формат 6084 116
Бумага типографская Плоская печать Усл. печ.л. 2,38
Уч.-изд. л. 1,4 Тираж Заказ Цена С
Редакционно-издательский отдел ГОУ ВПО УГТУ-УПИ
