75.Числовые ряды, признаки их сходимости. Абсолютно и условно сходящиеся ряды, их свойства.

Рядом называется последовательность .

Числовой ряд – выражение вида , где образуют бесконечную последовательность.

Суммы , назіваются частичными суммами ряда, а член - общим членом ряда. Если последовательность частичных сумм имеет предел (при n ) , то ряд называется сходящимся, а число - суммой ряда. Обозначение: . Если предела не существует, то ряд – расходящийся.

Необходимое условие сходимости ряда:

Если ряд сходится, то общий член ряда должен при стремится к нулю: .

Критерий Коши сходимости ряда:

Числовой ряд является сходящимся тогда и только тогда, когда для любого >0 существует такое N что для любого и для любого натурального p выполняется: .

Свойства сходящихся рядов:

1. Отбрасывание конечного числа начальных членов ряда или присоединение в начале его нескольких новых членов не отражается на поведении (сходимости или расходимости) ряда.

2. Если члены сходящегося ряда умножить на один и тот же множитель с, то его сходимость не нарушится.

3. Сходящиеся ряды можно почленно складывать и вычитать: из сходимости ряда с суммой и с суммой следует, что ряд сходится и его сумма равна .

Числовые ряды с положительными членами

, - числовой ряд с положительными членами.

Признаки сходимости:

1. Признак сравнения. Если два ряда и имеют положительные члены и, начиная с некоторого n, , то из сходимости первого ряда следует сходимость второго, а из расходимости второго ряда следует расходтмость первого.

2. Признак сравнения в предельной форме. Если существует придел . Тогда первый ряд эквивалентен второму (т.е. ведут себя одинаково).

3. Интегральный признак Коши-Маклорена. Пусть функция неотрицательна и не возрастает на [1,+ ), тогда ряд и ведут себя одинаково. (функция не возрастает на (а,b), если для любых и : : ).

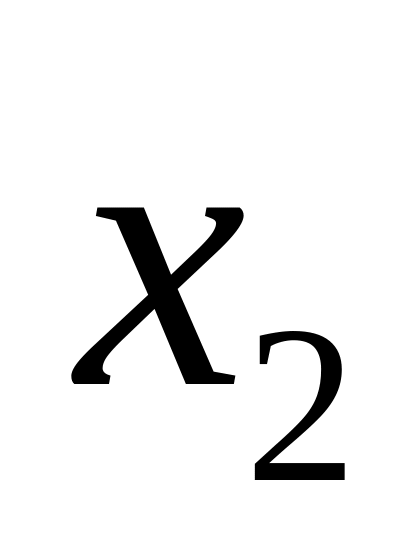
4. Признак Даламбера. 1) Если начиная с некоторого номера для любого выполняется ,то ряд – сходится, если это отношение , то ряд – расходится. 2) Если , то при - ряд сходится, при - ряд расходится, - нельзя сказать.

5. Признак Коши. 1) Если начиная с некоторого номера для любого выполняется 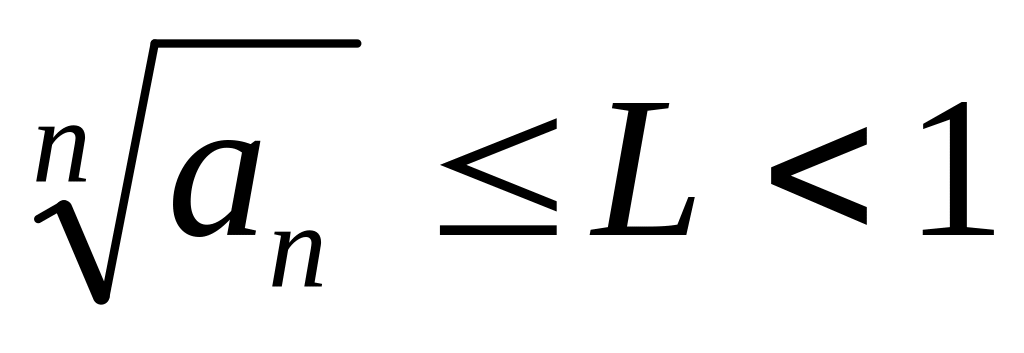,то ряд – сходится, если это отношение , то ряд – расходится. 2) Если , то при - ряд сходится, при - ряд расходится, - нельзя сказать.

Абсолютная и условная сходимость.

Одновременно с рядом , члены которого имеют неодинаковые знаки (знакопеременный ряд), удобно рассматривать ряд , составленный из абсолютных величин членов первого ряда. Если второй ряд сходится, то и первый сходится; в этом случае первый ряд называют абсолютно сходящимся. Если же второй ряд расходится, то первый ряд может расходится, но может и сходится; в последнем случае он называется условно сходящимся.

Свойства абсолютно сходящихся рядов.

1. В абсолютно сходящемся ряде члены можно переставлять местами любым способом; сумма ряда не будет при этом меняться. Переменив же порядок условно сходящегося ряда (т.ч. будет переставлено бесконечное множество членов ряда), можно изменить его сумму, сделать ее равной любому числу и даже сделать ряд расходящимся.

2. Абсолютно сходящиеся ряды можно не только почленно складывать и вычитать, но и перемножать, как обыкновенные многочлены, представляя результат в виде ряда.

Знакопеременные числовые ряды

, ≥0 – знакопеременный ряд.

Если - сходится    - сходится.

Признаки сходимости знакопеременных рядов:

1.Признак Дирихле. Пусть - ограничена, и пусть - монотонно стремится к 0. Тогда - сходится.

2.Признак Абеля. Пусть - ограничена, и пусть - монотонно и ограничена. Тогда - сходится.

3.Признак Лейбница. Пусть - монотонно стремится к 0 ( >0). Тогда - сходится.

Теорема Дирихле: Если ряд абсолютно сходится то любая его перестановка тоже абсолютно сходится к той же сумме.

Теорема Римана: Пусть - условно сходится. Тогда Для любого действительного А существует такая перестановка ряда , которая сходится к этому числу А.

Определения:

Предел переменной величины х – постоянное число а, если для каждого наперед заданного произвольно малого положительного числа можно указать такое значение переменной х, что все последующие значения переменной будут удовлетворять неравенству .

Предел функции . Функция при , если для каждого , как бы мало оно ни было, можно указать такое , что для всех и удовлетворяющих неравенству , имеет место неравенство . Если -предел функции при , то пишут .

Ограничпенная последовательность – если для заданной последовательности можно указать такое число , что все без исключения члены последовательности будут .

Монотонные: возрастающие, убывающие, неубывающие, невозрастающие.