46. Поверхности 2-го порядка.

Общее уравнение поверхности 2-го порядка имеет вид:

К числу поверхностей 2-го порядка относятся: эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, эллиптический параболоид, гиперболический параболоид, конус, цилиндры.

Приведем канонические ур-я этих поверхностей:

эллипсоид:

Если т. М(x,y,z) эллипсоиду, то ему также будут точки: (-x,-y,-z), (-x,y,z,),(x,-y,z),(x,y,-z),(-x,-y,z)…,а это значит, что т. О(0;0;0) явл. центом симметрии. Пл-ти ХОУ,ХОZ,YOZ явл. пл-ми симметрии и координатные оси явл. осями симметрии. Эллипсоид- поверхность огранниченная.

о днополостный гиперболоид: . т.О(0;0;0)- т. симметрии; координатные пл-ти х=0,у=0,z=0 – пл-ти симметрии, оси x,y,z – оси симметрии. Сечение гиперболоида х=0 пл-тью есть гипербола: ; у=0: . Если рассечь гиперболоид z=h, то получим: . Из сказанного выше получаем, что однополостный гиперболоид – неограниченная поверхность и имеет вид:

двуполостный гиперболоид: 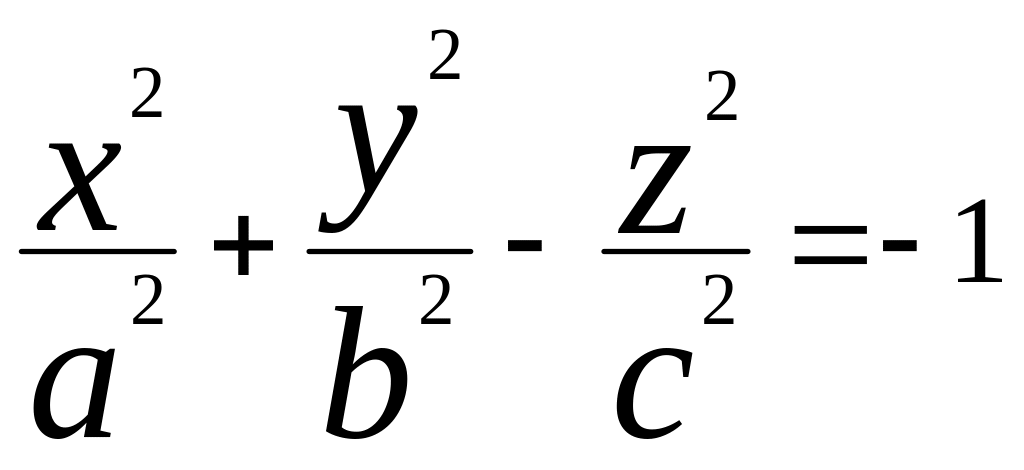. т. О(0;0;0)- центр симметрии; координатные пл-ти явл. пл-ми симметрии; координатные оси- осями симметрии. Если рассекать эту поверхность пл-ми z=h , , то при гиперболоид не будет иметь точек с секущими пл-ми. При двуполостный гиперболоид будет иметь 2 общие точки (0;0;с) и (0;0;-с). Если , то в сечении получим эллипс: . Если мы рассечем поверхность пл-тью х=0, то получим гиперболу:

; если у=0, то гиперболу: . Из сказанного выше двуполостный гиперболоид неограниченная поверхность и имеет вид:

э ллиптический параболоид: х,у: z 0. Значит, что данная поверхность лежит в полупространстве z 0. Счение данной поверхности пл.-ми z=h>0 представляет собой эллипс: . А сечение поверхности координатными плоскостями х=0 и у=0 будут явл. параболами. Эти пл-ти явл. пл-ми симметрии,

а z- осью симметрии. Данная поверхность неограниченная и имеет вид:

гиперболический параболоид: . Сечение поверхности пл-тью у=0 или х=0 явл. параболой;

а сечение параболоида пл-ми z=h , , представляет собой гиперболы: ^. Ось z- ось симметрии, а пл-ти х=0, у=0 – пл-ти симметрии. Поверхность неограниченная.

к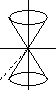 онус: . т. О(0;0;0)- центр симметрии, оси и пл-ти – оси и пл-ти симметрии. Сечение конуса пл-ми х=0 (у=0) представляет собой пару пересекающихся прямых, а сечение конуса пл-тью z=h представляет собой эллипс: . Имеет следующий вид:

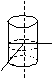
ц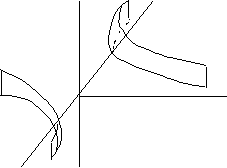 илиндры: а) эллиптический цилиндр

б) гиперболический цилиндр

в) параболический цилиндр у²=2рх

47.Повторение испытании. Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра и Лапласа.

Если проводится n испытаний, и вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания наз. независимыми относительно соб. А.

Повторные независимые испытания наз. испытаниями Бернулли, если при каждом испытании имеются только два возможных исходов и вероятности этих исходов остаются неизменными для всех испытаний. Одному испытанию Бернулли соответствует множество элементарных исходов состоящее из 2-х элемен. событий.

- неудача (0), - успех (1)

множество элементарных исходов для n испытаний состоит из 2ⁿ элемент. исходов , которые представляют собой последовательности состоящие из 0 и 1, соответствующие результату испытаний на каждом этапе.

Формула Бернулли. Вероятность того, что при n испытаниях событие А произойдет ровно m раз. И  не произойдет n-m раз выражает формула Бернулли.

.

Если число испытаний велико, а вероятность успеха мала, то вероятность m успехов в n испытаниях рассчитывается по формуле Пуассона.

Th. Пуассона. Если при и , так что , то вероятность m успехов в n испытаниях Бернулли вычисляется по формуле Пуассона:

. Условие применения формулы Пуассона:

При больших n пользуются локальной теоремой Муавра-Лапласа, которая дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события m раз из n испытаний, если число испытаний достаточно велико.

Th. Если вероятность Р появления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность P_n(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции:

при

Для вычисления функции имеются таблицы.

Пусть проводится n испытании, в каждом из которых вероятность события А появиться в n испытаниях не менее m₁ и не более m₂ раз, существует интегральная теорема Муавра- Лапласа: если вероятность Р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А появится в n испытаниях от m₁ до m₂ раз, приближенно равна определенному интегралу:

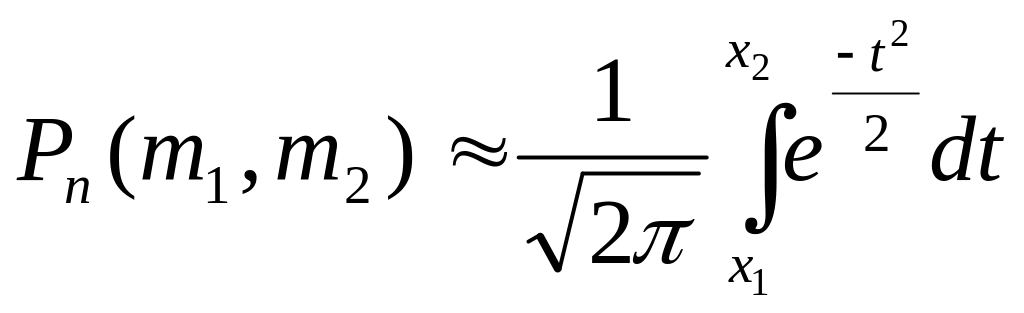, где ,

если npq<20, то .