17. Интегрирование фкп. Интеграл по замкнутому контуру от аналитической функции. Интегральная формула Коши и следствия из нее.
Путь(кривая) на плоскости – непрерывный образ вещественного отрезка: z = z(t)
Если функция
является взаимнооднозначной, то кривая
наз. Жордановой
-
- кривая без самопересечений.
Условия гладкости:
-кривая.
Гладкая Жорданова кривая наз. контуром.
Интеграл Римана.
Пусть есть
непрерывная в обл.D
и
- спрямляемый контур.
Разобъем дугу на n частей:
Тогда
- интегральная сумма,
,
Вычисляется:
1)
2)
Свойства :
1.Линейность
2.Аддитивность
3.Ориентируемость
4.Оценка
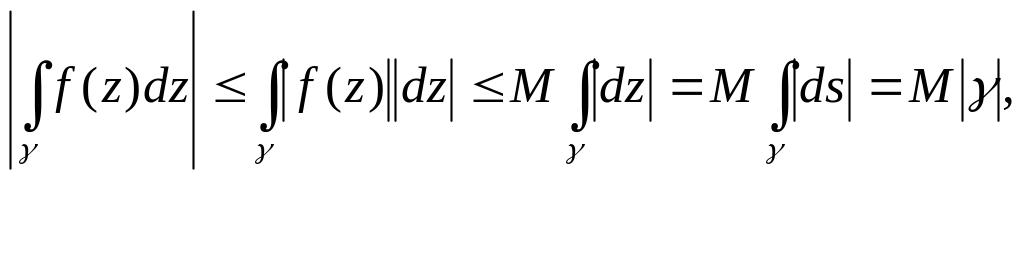
где: f(z)
– непрерівна на
(компакте), значит достигает на нем
наибольшего по модулю значения.
ds – дифференциал дуги
Интеграл по замкнутому контуру:
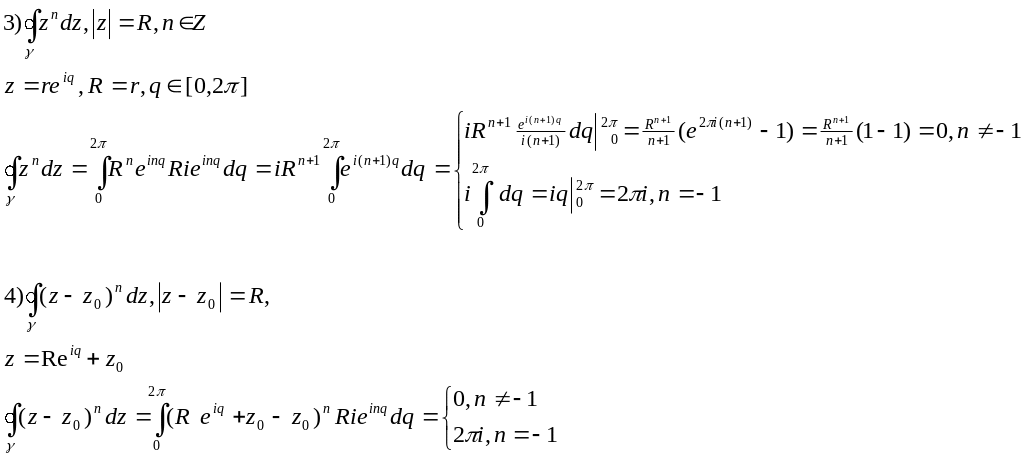
Лемма1
- аналитична в
треугольнике
тогда
Лемма2
- аналитична в
n-угольнике
т
огда
Лемма 3 P D
- непрерывна в области D; - спрямляемый контур.
Тогда
- вписанная в контур ломанная, такая что
Теорема (интегральная теорема Коши).
- аналитична в
.
Тогда
Предложение1:
Пусть f(z)
– аналитична в
.
Тогда
Предложение 2:
Предложение 3:
Пусть f(z) – аналитична в .
|f(z)|
.
Тогда
Теорема
(интегральная формула Коши): Пусть
f(z)
– аналитична в
.Тогда
:
.
Следствия:
Теорема Лиувилля:
Пусть f(z)
– аналитична в С и |f(z)|
(ф-я
ограничена всюду)
Тогда f(z) – константа.
Основная теорема высшей алгебры:
Пусть многочлен
Тогда
Теорема о среднем:
Пусть f(z)
– аналитична в
.
Тогда
18. Интерполирование функций. Интерпол. Полином лагранжа
Задача определ. произвольной функции либо интеграла от ф.-ии y=f(x) по заданным дискретным значениям yі=f(xі ) использует понятие апроксимации ф.-ии. Аппроксимация также использ.-ся при построении сеточных уравнений.
Суть задачи аппроксимации зал. в след. Пусть дана некот. неизвестная в аналитическом смысле ф.-ия y=f(x), и известно лишь ее поведение на отрезке [a, b]. Такую ф.-ию наз. аппроксимируемой. Требуется построить другую ф.-ию y=F(x), наз. аппроксимирующей ф.-ией, которая была бы близка к ф.-ии y=f(x) некот. погрешностью. Т.е. задача аппроксимации сост. в том, чтобы по зад. значениям ф.-ии y=f(x) в нескольких точках отрезка [a, b], получить ее значения в остальных точках этого отрезка. При этом необх. выполнение след.:
задание дискретных значений ф.-ий yі=f(xі )
класс аппроксир.-щих ф.-ий, из кот. конструируется ф.-ия y=F(x)
вид критерия согласия между ф.-ями y=f(x) и y=F(x)
оценка погрешности аппроксимации
Вид задания ф.-ии y= F (x) зависит от класса решаемых задач. При исследовании напряженно-деформированного состояния по методу конечных элементов в задачах механики деформир.-го тела аппроксим.-щие ф.-ии предст.-ся комбинацией ф.-ий 1,х,…,хп, либо сплайнами.
Критерий согласия либо близости аппрокс.-мой и аппрокс.-щей ф.-ий опр.-ся из условия минимума расстояний между ними. Например, самым распространенным критерием явл. критерий Чебышева:
Другой критерий (метод наименьших квадратов)может быть записан в виде:
В
опросы
оценки погрешности зависят от трех
первых требований и рассм.-ся отдельно
для каждого случая аппроксимации.
Геометр. процесс интерполяции:
Если f(x) и F(x) совпадают в узлах аппроксимации, то этот вид аппрок.-ии наз. интерполируемым. Если же х[a, b], то имеет место интерполяция, х [a, b], то имеет место экстраполяция.
При = 0 в узлах интерполяции значение интерп.-мой и интерп.-щей ф.-ии совпадают, т.е. f(xі )= F (xі), (1)
a0 + a1 xi 1+a2 xi2+…+anxi n= f(xi). (2)
В этом случае F(x)
– интерполирующий полином порядка n 
,
коэф.-ты ак – неизвестны . Они нах.-ся из равенства (1), что эквив.-но (2).
a0 + a1 xi 1+a2 xi2+…+anxin = f(xi) (і=0, 1, 2,…,n)
Получим матрицу:
-
определитель Вандермонда
W0, если нет несовпадаемых условий, то из системы (2) всегда можем найти ак, т.е. построить интерпол. полином.
Интерполяц.
полином Лагранжа.
Задача: найти F(x),
надо
знать аі.Эта
задача трудна, но можно ее обойти.
Ln
(x)-
полином Лагранжа, n
– порядок (n=1,2,..).
При n=1
– полином 1-го порядка,…., n-го
порядка: 
. (1)
Интерпол. полином представляется через значения самой ф.-ии в узлах интерполирования. Ск(х) – коэф.-ты разложения. Удовлетворяя услов. Чебышева:
(2) Ск(х)
обладают
свойством:
(3)
Ск(х) = к(х-х0)(х-х1)…(х-хк-1)(х-хк+1)…(х-хп) (4).
Учитывая (4), к=1 (хк – х0)(хк – х1)…(хк – хп). Подставив к в (3), (3) в (2) – получим интерпол. полином Лагранжа:
.
Чаще всего применяется линейная интерполяция при n=1
