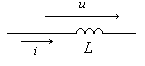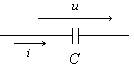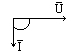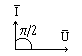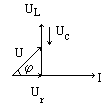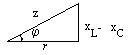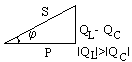Программа работы

1. Изучить схему замещения экспериментальной цепи (рис. 6.1)

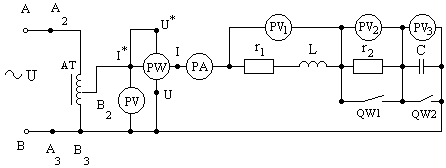
Рис. 6.1

2. Измерить и рассчитать параметры цепи для трех опытов (табл. 6.1):

а) включена реальная катушка индуктивности (выключатели QW₁ и QW₂ замкнуты);

б) включены катушка и активное сопротивление (QW₁ разомкнут, QW₂ замкнут);

в) включены катушка, активное сопротивление и конденсатор (QW₁ и QW₂ разомкнуты).

3. Вычислить параметры цепи и построить в масштабе векторные диаграммы напряжений и тока для каждого опыта, а также треугольники мощностей.

4. Рассчитать емкость конденсатора для получения резонанса напряжений при последовательном включении катушки и конденсатора, а также напряжения на элементах схемы для этого варианта.

Таблица 6.1

№ опыта

Измерено

Вычислено

Р

U

I

U1

U2

U3

Ur1

UL

Ur2

UC

P

Q

S

Вт

В

А

В

В

В

В

В

В

В

Вт

ВАр

ВА

1

2

3

Теоретические положения

На переменном токе различают три вида идеальных сопротивлений, определяющих различный характер электромагнитных процессов в таких цепях: активное r, индуктивное x_L и емкостное х_С. Последние два называются реактивными сопротивлениями. Это позволяет реальные приемники электроэнергии изображать схемами замещения в виде соединения идеальных сопротивлений и проводить электротехнические расчеты, отражающие суть физических процессов в цепях переменного тока.

Идеальное активное сопротивление r. Это приемники, для которых можно пренебречь наличием переменных магнитных полей и связанных с этим явлений самоиндукции и скинэффекта (вытеснение тока из центра проводника к поверхности, в результате чего сопротивление возрастает); а также пренебрегаем возможностью накапливания электрических зарядов. В таком сопротивлении напряжение и ток совпадают по фазе, электрическая энергия безвозвратно превращается в другой вид энергии (тепло, свет и др.). Примерами таких сопротивлений являются лампы накаливания, резисторы, нагреватели. Потребляемая ими средняя мощность за период называется активной и измеряется в ваттах (Вт): P = U_r · I.

Идеальное индуктивное сопротивление x_L. Если на сердечник из ферромагнитного материала намотать катушку из сверхпроводника (r = 0), включит в цепь переменного тока, то в связи с появлением ЭДС самоиндукции величина тока будет ограничена, а ток отстает по фазе от напряжения U_L на 90 электрических градусов. Мгновенная мощность р изменяется с двойной частотой. Средняя мощность за период Р равна нулю. Четверть периода мощность потребляется из сети, превращаясь в энергию магнитного поля, а во вторую четверть возвращается в сеть, преобразуясь в электрическую энергию. Амплитудное значение мощности за четверть периода называется реактивной мощностью (Q_L = U_L · I) измеряется в ВАр (вольт-ампер реактивный).

Идеальное емкостное сопротивление x_С. При включении в цепь переменного тока конденсатора амперметр покажет постоянное наличие тока в цепи. Это не означает, что ток проходит через изоляцию между обкладками конденсатора. Это будет пробой конденсатора. Физика процессов заключается в том, что четверть периода конденсатор заряжается, потребляя энергию из сети, а вторую четверть разряжается, отдавая энергию обратно в сеть, т.е. энергия циркулирует между генератором и приемником так же, как в идеальном индуктивном сопротивлении с двойной частотой. Средняя мощность за период Р равна нулю, а амплитудная за четверть периода (Q_C = U_C · I) также называется реактивной. Ток в такой цепи опережает напряжение U_C на 90 электрических градусов. Напряжения U_L и U_C, а также реактивные мощности Q_L и Q_C находятся в противофазе (сдвинуты друг относительно друга во времени на 180 электрических градусов).

Реальные сопротивления. В реальных приемниках электроэнергии на переменном токе наблюдаются одновременно все те физические процессы, которые отмечены для идеальных сопротивлений. Степень возможностей идеализации определяется требуемой точностью инженерных расчетов. С учетом этого реальные приемники можно представить в виде схемы замещения, состоящей из идеальных сопротивлений. При их последовательном соединении ток в цепи одинаков, напряжение на участке цепи находится по закону Ома, напряжение на нескольких элементах определяется векторной суммой напряжений участков.

Характеристики участков цепи переменного тока при последовательном соединении элементов приведены в таблице 6.2. В общем случае в результате векторного сложения напряжений по участкам цепи образуется треугольник напряжений; разделив его стороны на ток, получим треугольник сопротивлений, а умножив на ток – треугольник мощностей. По ним находятся формулы для расчета неизвестных параметров.

Таблица 6.2

Характеристики	Идеальное активное сопротивление	Идеальное индуктивное сопротивление	Идеальное емкостное сопротивление	Последовательное соединение r, L, C-элементов
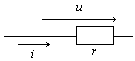
1. Изображение и обозначение
2. Связь между током и напряжением
3. Выражение мгновенных значений напряжения тока	u = Um · sinω t i = Im · sinω t	u = Um · sinω t i= Im · sin(ωt – )	u = Um · sinω t i = Im · sin(ωt+ )	u = Um · sinω t i = Im · sin(ωt φ)
4. Векторная диаграмма	φ = 0	π / 2 φ = π / 2 – отстающий	φ = π / 2 – опережающий	UL>UC φ >0
5. Формула для определения сопротивления		хL=ωL
6. Закон Ома для участка цепи
7. Коэффициент мощности
8. Мощность	активная P = I 2r = UrI	реактивная QL = I 2 · xL = ULI	реактивная QC = I 2 · xC = UC I	полная

Резонанс напряжений. Если x_L = x_C, то полное сопротивление цепи будет минимальным z = r, ток – максимальным, а U_L = U_C, U = U_r. Это состояние цепи называется резонансом напряжений.

При x(L,C) >> r напряжения на реактивных элементах L, C будут значительно превышать напряжение сети. Это используется в телеуправлении, автоматике для выделения полезного сигнала.

Резонанс напряжений возможен при любых параметрах L, C при определенной частоте тока, называемой резонансной ω:

x_L = x_C .

где .

Из этих же соотношений при известной частоте тока и величины одного из параметров (L или C) можно рассчитать величину второго параметра для получения резонанса.

В электротехнике последовательное соединение r, L, C-элементов встречается, например, в конденсаторных двигателях, причем индуктивное сопротивление обмотки и соответственно напряжение обычно на порядок больше ее активного сопротивления. При резонансе повышение напряжения на обмотке и конденсаторе может быть опасным как для оборудования, так и для персонала.