Глава 2. Расчет сложных цепей постоянного тока

Сложная цепь имеет два и более источника ЭДС, и направление токов нельзя определить без расчета.

Основные определения и законы Кирхгофа:

1. Ветвь – участок цепи с последовательным соединением элементов.

2. Узел – точка соединения нескольких ветвей.

3. Контур – любой замкнутый путь по цепи с началом и концом в одном узле.

4. Независимый контур – отличается от другого хотя бы одной ветвью.

I закон Кирхгофа.

Алгебраическая сумма токов, сходящихся в узле, равна нулю, или сумма токов, подходящих к узлу, равна сумме токов, выходящих из узла:

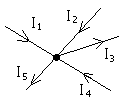
I₁ + I₂ – I₃ + I₄ – I₅ = 0;

или

I₁ + I₂ + I₄ = I₃ + I₅.

II закон Кирхгофа. В любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений.

.

Правило выбора знака: если ЭДС, ток совпадают с направлением обхода контура, берутся со знаком “плюс”, не совпадают – “минус”.

Методика расчета с использованием законов Кирхгофа

1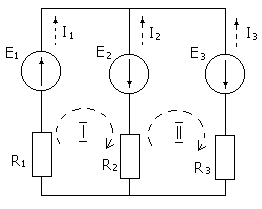 . Выбираем независимые контуры, например, I и II, произвольно задаемся направлением их обхода и направлением токов в ветвях (отмечено пунктиром).

2. Составляем (n – 1) уравнений по I закону, где n – число узлов, а недостающее число уравнений – по II закону.

3. Получаем систему уравнений:

Решаем, находим токи в ветвях. Если ток получился со знаком “минус”, значит он протекает в противоположном направлении.

4. Проверка правильности решения определяется соблюдением I закона Кирхгофа и баланса мощностей.

Необходимо иметь в виду, что источники ЭДС могут работать в режиме генератора (направления тока и ЭДС совпадают) и быть потребителем энергии, если такого совпадения нет.

Метод контурных токов

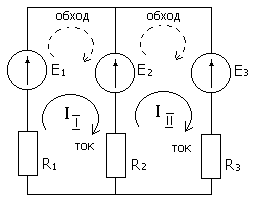
1. Определяемся с числом независимых контуров и считаем, что в каждом контуре проходит свой контурный ток. Произвольно задаемся их направлениями и направлением обхода контуров (берем все по часовой стрелке).

2. Составляем уравнения по II закону Кирхгофа для выбранных контуров с учетом того, что по некоторым ветвям проходят токи нескольких контуров, а для каждого контура имеем последовательное соединение элементов.

Имеем:

E₁ – E₂ = I_I (R₁+R₂) – I_IIR₂;

E₂ – E₃ = I_II (R₂+R₃) – I_IR₂.

3. Решаем систему уравнений, определяем контурные токи. Если ток получился со знаком “минус”, значит фактически он имеет противоположное направление.

Токи в ветвях определяем по соотношениям:

I₁ = I_I; I₃ = I_II; I₂ = I_I-I_II

4. Проверка: I-й закон Кирхгофа и баланс мощностей.

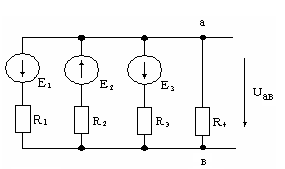
Метод узлового напряжения (двух узлов)

Если электрическая цепь состоит только из параллельных ветвей, т.е. имеет всего два узла, напряжение между которыми называется узловым (U_aв), то его можно определить в общем случае по формуле:

,

где E_i – ЭДС; g_i = 1/R_i – проводимость ветви.

ЭДС ветви берется со знаком “плюс”, если направлено к узлу, обозначенному первым индексом (а), и со знаком “минус”, если направлено ко второму узлу.

В нашем случае имеем:

.

Зная узловое напряжение, можно каждую ветвь рассматривать в отдельности и определить токи.

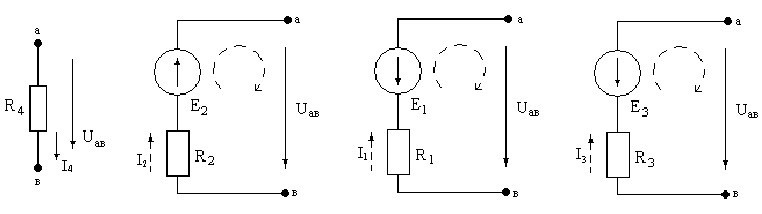
Для пассивной ветви (где нет источника ЭДС) направление тока совпадает с направлением узлового напряжения, а для активных ветвей задаемся произвольно направлениями токов и составляем уравнения по II закону Кирхгофа:

-E₁ = U_aв + I₁R₁; E₂ = U_aв + I₂R₂; -E₃ = U_aв + I₃R₃,

откуда определяем токи:

I₁ = (-U_aв – E₁)g₁; I₂ = (E₂ - U_aв)g₂; I₃ = (–E₃ - U_aв)g₃.

Кроме рассмотренных применяются и другие методы расчета сложных цепей.

Примеры решения задач

2.1. В цепи ЭДС источников питания равны Е₁, Е₂, Е₃, а сопротивления ветвей – соответственно r₁, r₂, r₃, r₄ (включая внутренние сопротивления источников питания). Определитеь силы токов во всех ветвях цепи и режим работы каждого из источников. Составьте баланс мощностей. Задачу решите двумя методами: узлового напряжения и контурных токов.

Вариант	Данные к задаче № 1
	Е1, В	Е2, В	Е3, В	r1, Ом	r2, Ом	r3, Ом	r4, Ом
1	220	150	120	5	4	2	1

Р е ш е н и е. Определяем силы токов во всех ветвях цепи методом двух узлов. Предварительно направим все токи из узла «а».

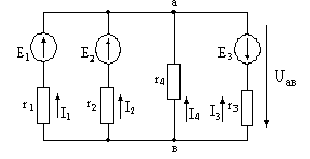
Рис. 2.1

Определим напряжение между узлами «ав»:

, (1)

где E_i – ЭДС;

g_i = 1/R_i – проводимость ветви.

Определим токи в ветвях:

Если направления токов и ЭДС совпадают, то источник ЭДС работает в режиме генератора, если нет – потребителя. Так как все токи совпадают с ЭДС, то все источники ЭДС работают в режиме генератора.

Составим баланс мощностей:

;

;

кВт;

;

Вт.

Баланс мощностей соблюдается.

Определим токи в ветвях методом контурных токов:

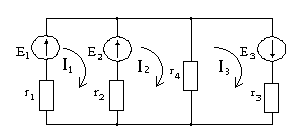
Выбираем контуры: I – r₁E₁E₂r₂; II – r₂E₂r₄; III – r₄E₃r₃.

Направления обхода и токов выбираем произвольно (по часовой стрелке). Составим уравнения по II закону Кирхгофа для каждого контура:

Применим правило Крамера:

Определим токи в ветвях:

I₁ = I_I = 41,8 A;

I₂ = I_II – I_I = 76,5 – 41,8 = 34,7 A;

I₃ = I_III = 65,5 A;

I₄ = I_II – I_III = 76,5 – 65,5 = 11 A.

Значения токов совпадают с предыдущим расчетом. Задача решена правильно.