13. Метод Зейделя
Метод Зейделя представляет собой некоторую модификацию метода итерации. Основная его идея заключается в том, что при вычислении (к+1)-го приближения неизвестной х учитываются уже вычисленные ранее (к+1)-го приближения неизвестных
х
,
х
… х
Например х =а * х +а *х
х =а * х +а *х
Пример: Метод Зейделя решить систему с точностью до 0,001
4,5х -1,8х +3,6х =-1,7
3,1х +2,3х -1,2х =3,6
1,8х +2,5х +4,6х =2,2
Решение: приведем систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк:
7,6х +0,5х +2,4х =1,9 [(1)+(2)]
2,2х +9,1х +4,4х =9,7 [2*(3)+(2)-(1)]
-1,3х +0,2х +5,8х = -1,4 [(3)-(2)]
Теперь в левой части оставляем 10х , а оставшиеся компоненты переносим в правую часть:
10х =2,4х -0,5х -2,4х +1,9
10х = -2,2х +0,9х -4,4х +9,7
10х =1,3х -0,2х -4,2х -1,4
Теперь каждое уравнение делим на 10:
х =0,24х -0,05х -0,24х +0,19
х = -0,22х +0,09х -0,44х +0,97
х =0,13х -0,02х -0,42х -0,14
для начала выбираем нулевые приближения (за нулевые приближения берем свободные члены):
х =0,19; х =0,97; х = -0,14.
Теперь вычисляем первые приближения:
х =а *х +а *х +а *х +b =0,24*0,19-0,05*0,97-0,24*(-0,14)+0,19=0,2207
х =а *х +а *х +а *х +b = -0,22*0,2207+0,09*0,97-0,44*(-0,14)+0,97=1,0703
х =а *х +а *х +а *х +b =0,13*0,2207-0,02*1,0703-0,42*(-0,14)-0,14= - 0,1915
Затем вычисляем вторые приближения, третьи и т.д. До тех пор пока последующее значение корня минус предыдущее не станет меньше 0,001
Реализация данного метода в среде Excel
Заполним исходные данные системы как показано на рисунке 10.2
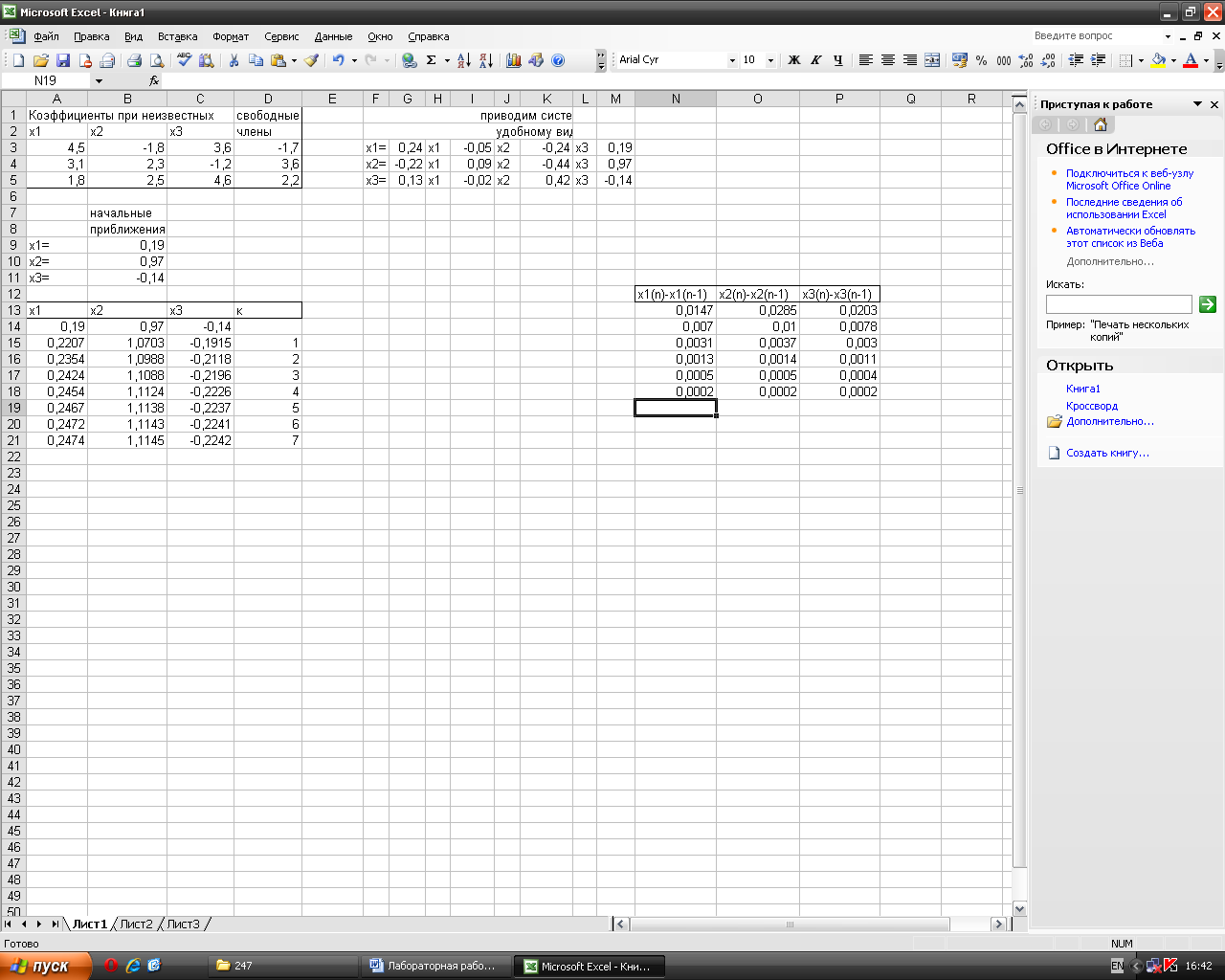
Рисунок 10.2
Коэффициенты исходной системы вносим в ячейки блока A3:D5. В ячейки блока B9:B11 записываем начальные приближения, которые равны свободным членам. В ячейки блока A14:C14 записываем последующие приближения:
Для х : А15=$G$3*A14+$I$3*B14+$K$3*C14+$M$3;
Для х : B15=$G$4*A15+$I$4*B14+$K$4*C14+$M$4;
Для х : С15=$G$5*A15+$I$5*B15+$K$5*C14+$M$5;
Затем копируем данные формулы:
A15 в A16; B15 в B16; C15 в C16;
Проделываем эти операции до тех пор, пока |x -x |<=0.001; |x -x |<=0.001; |x -x |<=0.001; |x -x |<=0.001;
Данная разность вычисляется в ячейках блока N14:P14
Для х : N14=ABS(A15-A14);
Для х : O14=ABS(B15-B14);
Для х : P14=ABS(C15-C14);
Затем копируем данные формулы: N14 в N15; O14 в O15; P14 в P15;
Ответ: х =0,247; х =1,114; х = -0,224
Задания для самоконтроля: решить систему с точностью до 0,001
М етод итерации
х =0,32х -0,18 х +0,02 х +0,21 х +1,83
А) х =0,16х +0,12 х -0,14 х +0,27 х -0,65
х =0,37х +0,27х -0,02 х -0,24 х +2,23
х =0,12х +0,21х -0,18 х +0,25 х -1,13
х =0,42х-0,32 х 0,03 х +0,44
х =0,11х -0,26х -0,36 х +1,42
Б) х =0,12х +0,08х -0,14 х -0,24 х -0,83
х =0,15х -0,35х -0,18 х -1,42
х
=0,18х
-0,34х
-0,12
х
+0,15
х
-1,33
В) х =0,11х +0,23х -0,15 х+0,32 +0,84
х =0,05х -0,12х +0,14 х -0,18 х -1,16
х =0,12х +0,08х 0,06 х +0,57
х =0,13х +0,23х -0,44 х -0,05 х +2,13
Г) х =0,24х -0,31 х +0,15 х -0,18
х =0,06х -0,15х -0,23 х +1,44
х =0,72х -0,08х -0,05 х +2,42
Метод Зейделя
3,7х -3,1х +4,0х =5,0
А) 4,1х +4,5х -4,8х =4,9
-2,1х +3,7х +1,8х =2,7
3,3х -3,7х -4,2х =5,8
Б) 2,7х +2,3х -2,9х =8,1
4,1х +1,8х +5,0х = -1,9
Лабораторная работа №11.
Тема: Интерполирование функций.
Формула Лагранжа для неравноотстоящих значений аргумента.
Пример 1.Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана в неравноотстоящих узлах таблицы.
Условия задачи:
х |
у |
0,05 |
0,050042 |
0,10 |
0,100335 |
0,17 |
0,171657 |
0,25 |
0,255342 |
0,30 |
0,309336 |
0,36 |
0,376403 |
Вычислить значение функции f(x) = y(x) при х = 0,263.
Решение:
Для
вычисления f(x)
необходимо воспользоваться формулой
f(x)
≈ Пn+1*
(yi
/Di),
где
Пn+1 =(x-x0)*(x-x1)*…*(x-xn)
Di = (xi-x0)*(xi-x1)*…*(xi -xi-1)*(x-xi)*(xi –xi+1)*…*(xi –xn).
Все вычисления произведем по таблице(рис.11.1):
i |
Разности |
Di |
yi /Di |
|||||
0 |
(x-x0) |
(x-x0) |
(x0-x2) |
(x0-x3) |
(x0-x4) |
(x0-x5) |
Сумма по 0-строке |
|
1 |
(x1-x0) |
(x-x1) |
(x1-x2) |
(x1-x3) |
(x1-x4) |
(x1-x5) |
Сумма по 1-строке |
|
2 |
(x2-x0) |
(x2-x1) |
(x-x2) |
(x2-x3) |
(x2-x4) |
(x2-x5) |
Сумма по 2-строке |
|
3 |
(x3-x0) |
(x3-x1) |
(x3-x2) |
(x-x3) |
(x3-x4) |
(x3-x5) |
Сумма по 3-строке |
|
4 |
(x4-x0) |
(x4-x1) |
(x4-x2) |
(x4-x3) |
(x-x4) |
(x4-x5) |
Сумма по 4-строке |
|
5 |
(x5-x0) |
(x5-x1) |
(x5-x2) |
(x5-x3) |
(x5-x4) |
(x-x5) |
Сумма по 5-строке |
|
Рисунок 11.1
Т.е. вычисляются как:
D0 = (x-x0)* (x-x0)* (x0-x2)* (x0-x3)* (x0-x4)* (x0-x5);
D1 = (x1-x0)* (x-x1)* (x1-x2)* (x1-x3)* (x1-x4)* (x1-x5);
D2
=
(x2-x0)*
(x2-x1)*
(x-x2)*
(x2-x3)*
(x2-x4)*
(x2-x5);
D3 = (x3-x0)* (x3-x1)* (x3-x2)* (x-x3)* (x3-x4)* (x3-x5);
D4 = (x4-x0)* (x4-x1)* (x4-x2)* (x4-x3)* (x-x4)* (x4-x5);
D5 = (x5-x0)* (x5-x1)* (x5-x2)* (x5-x3)* (x5-x4)* (x-x5);
Производя эти вычисления, получим следующую таблицу(рис.11.2)
i |
Разности |
Di |
y/Di |
|||||
0 |
0,213 |
-0,05 |
-0,12 |
-0,2 |
-0,25 |
-0,31 |
-1,9809Е-05 |
-2526,23 |
1 |
0,05 |
0,163 |
-0,07 |
-0,15 |
-0,2 |
-0,26 |
4,4499Е-06 |
22547,7 |
2 |
0,12 |
0,07 |
0,093 |
-0,08 |
-0,13 |
-0,19 |
-1,54365Е-06 |
-111202 |
3 |
0,2 |
0,15 |
0,08 |
0,013 |
-0,05 |
-0,11 |
1,716Е-07 |
1488007 |
4 |
0,25 |
0,2 |
0,13 |
0,05 |
-0,037 |
-0,06 |
7,215Е-07 |
428740,1 |
5 |
0,31 |
0,26 |
0,19 |
0,11 |
0,06 |
-0,097 |
-9,80402Е-06 |
-38392,7 |
Рисунок 11.2
Итак,
П5+1 = 0,213*0,163*0,093*0,013*(-0,037)*(-0,097)= 1,50649Е-07= 0,150649*10-6.
(yi
/Di)=
-2526,23+25547,7-111202+1488007+428740,1-38392,7= 1787173,95.
Теперь непосредственно вычисляем
f(0,263)= П5+1* (yi /Di)= 0,150649*10-6 * 1787173,95= 0,26924.
Ответ: 0,26924.
Реализация в среде Excel.
Заполним исходные данные системы как показано на рисунке 11.3.
В ячейку А9 вносим значение х.
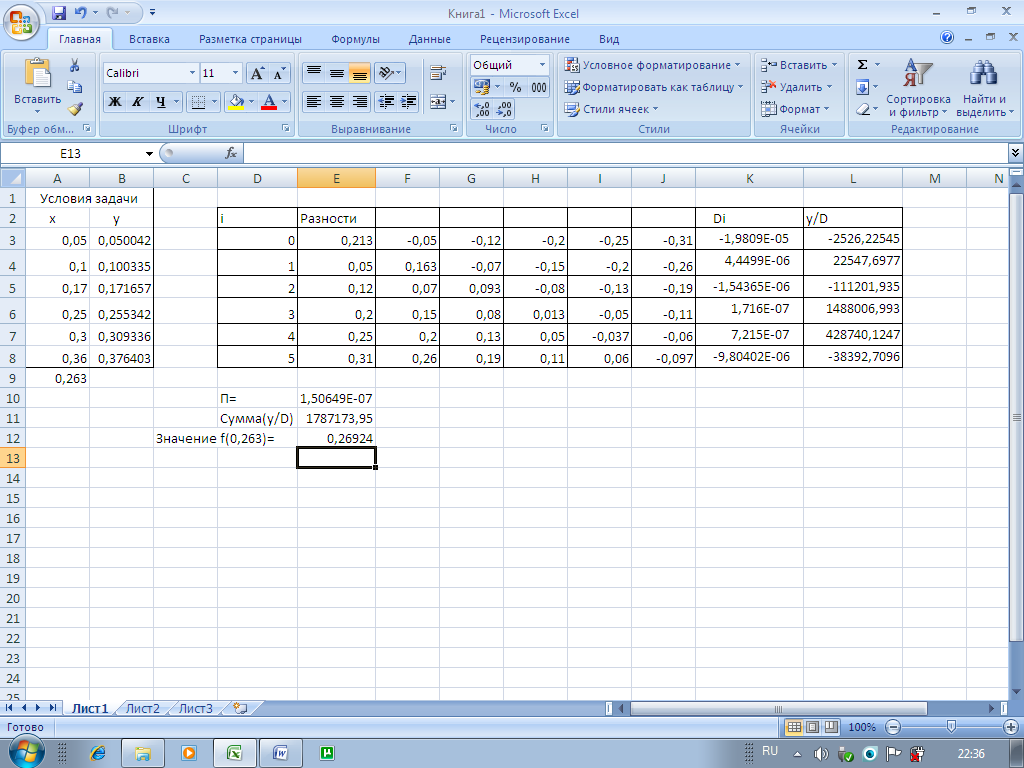
Рисунок 11.3
Данную таблицу заполняем согласно таблице (рис.11.1).
По диагонали вычисляем значения (х – хi),чтобы затем определить Пn+1
E3=A9+A3;
F4= A9+A4;
G5= A9+A5;
H6= A9+A6;
I7= A9+A7;
J8= A9+A8;
Теперь заполняем ячейки, которые находятся ниже диагонали:
E4=A4-$A$3……………………Копируем эту формулу в ячейки Е5, Е6, Е7 и Е8.
F5= A5-$A$4………………….. Копируем эту формулу в ячейки F6, F7, F8.
G6= A6-$A$5………………….. Копируем эту формулу в ячейки G7, G8.
H7= A7-$A$6…………………… Копируем эту формулу в ячейки H8.
I8= A8-$A$7.
Теперь заполняем ячейки, которые находятся выше диагонали:
F3=$A$3-A4
G3=A3-$A$5……………………Копируем эту формулу в ячейку G4.
H3= A3-$A$6………………….. Копируем эту формулу в ячейки H4,H5.
I3= A3-$A$7………………….. Копируем эту формулу в ячейки I4, I5, I6.
J3= A3-$A$8…………………… Копируем эту формулу в ячейки J4, J5, J6, J7.
Теперь определяем Di
K3=E3*F3*G3*H3*I3*J3 Копируем эту формулу в ячейки К4, К5, К6, К7, К8.
Определяем yi /Di
L3=B3/K3 Копируем эту формулу в ячейки L4, L5, L6, L7, L8.
Определяем Пn+1
E10=E3*F4*G5*H6*I7*J8= 1,50649Е-07.
Определяем (yi /Di)
Е11=СУММ(L3:L8)= 1,7872Е+06.
Теперь непосредственно вычисляем f(0,263)= П5+1* (yi /Di)
Е12=Е10*Е11=0,26924.
Ответ:0,26924.
Формула Лагранжа для равноотстоящих значений аргумента.
Пример 1. Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лагранжа, если функция задана в равноотстоящих узлах таблицы.
Условия задачи:
х |
у |
0,101 |
1,26183 |
0,106 |
1,27644 |
0,111 |
1,29122 |
0,116 |
1,30617 |
0,121 |
1,32130 |
0,126 |
1,32660 |
Вычислить значение функции f(x)=y(x) при х = 0,1157.
Решение:
Для
вычисления f(x)
необходимо воспользоваться формулой
f(x)≈Пn+1(t)*
,
где Пn+1(t)
= (t-0)*(t-1)*…*(t-n);
t=(x-x0)/h;
h=xi+1
-
xi
– шаг
интерполяции.
Ci = (-1)n-1 *i! * (n-i)!.
Здесь h=0,106-0,101= 0,005
t=(0,1157-0,101)/0,005= 2,94
Все вычисления произведём по таблице(рис.11.4)
I |
t-i |
Ci =(-1)n-1 *i!*(n-i)! |
(t-i)*Ci |
yi /((t-i)*Ci) |
0 |
t-0=2,94-0=2,94 |
(-1)5-0*0!*(5-0)!=-120 |
2,94*(-120)= -352,8 |
|
1 |
t-1=2,94-1=1,94 |
(-1)5-1*1!*(5-1)!=24 |
1,94*24=46,56 |
|
2 |
t-2=2,94-2=0,94 |
(-1)5-2*2!*(5-2)!=-12 |
0,94*(-12)= -11,28 |
|
3 |
t-3=2,94-3=-0,06 |
(-1)5-3*3!*(5-3)!=12 |
-0,06*12= -0,72 |
|
4 |
t-4=2,94-4=-1,06 |
(-1)5-4*4!*(5-4)!=-24 |
-1,06*(-24)=25,44 |
|
5 |
t-5=2,94-5=-2,06 |
(-1)5-5*5!*(5-5)!=120 |
-2,06*120= -247,2 |
|
Рисунок 11.4.
В результате вычислений получаем следующую таблицу (рис.11.5)
i |
t-i |
Ci |
(t-i)*Ci |
yi /((t-i)*Ci) |
0 |
2,94 |
-120 |
-352,8 |
-0,0035766 |
1 |
1,94 |
24 |
46,56 |
0,0274149 |
2 |
0,94 |
-12 |
-11,28 |
-0,1144699 |
3 |
-0,06 |
12 |
-0,72 |
-1,8141250 |
4 |
-1,06 |
-24 |
25,44 |
0,0519379 |
5 |
-2,06 |
120 |
-247,2 |
-0,0053665 |
Рисунок 11.5
Итак П5+1(t)= 2,94*1,94*0,94*(-0,06)*(-1,06)*(-2,06)= -0,7024271
= -0,0035766 *(0,0274149)*(-0,1144699)*(-1,8141250)*(0,0519379)*(0,0053665) = -1,858185
Следовательно, = -0,7024271*(-1,858185)= 1,30524
Ответ: 1,30524.
Реализация в среде Excel.
Заполним исходные данные системы как показано на рисунке 11.6.
В ячейку А9 вносим значение х.
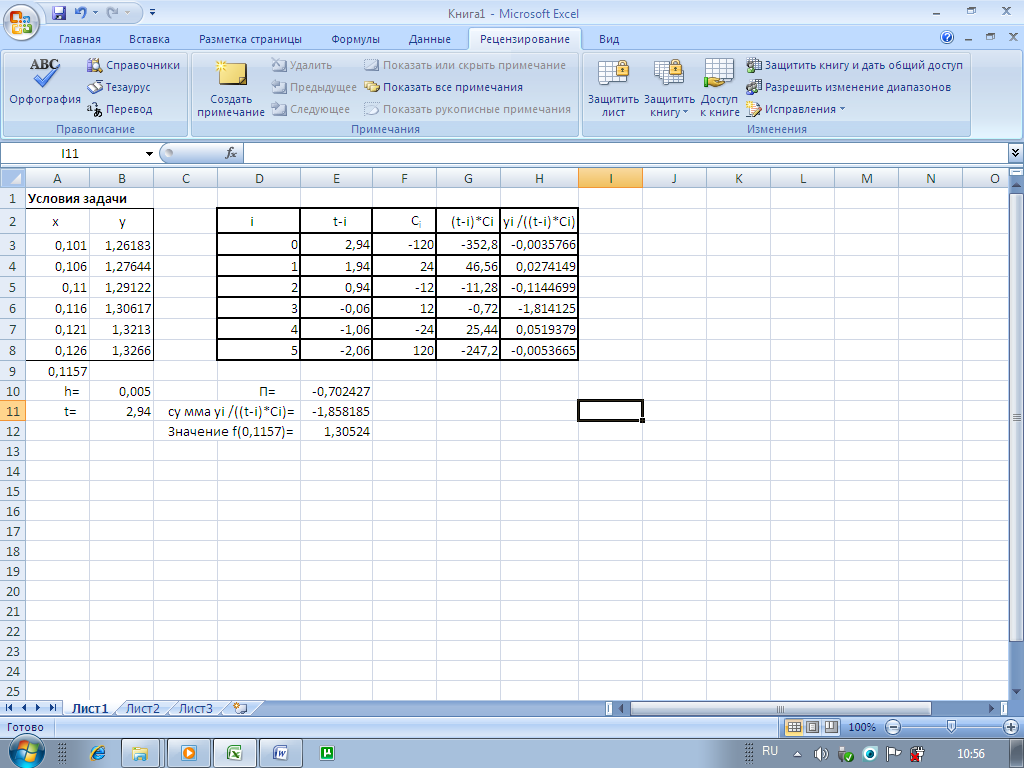Рисунок
11.6
Данную таблицу заполняем согласно условию задачи.
Для начала вычислим (t-i):
Е3=$B$11-D3……….Копируем эту формулу в ячейки Е4,Е5,Е6,Е7,Е8.
Теперь вычислим Ci
F3=((-1)^(5-D3))*ФАКТР(D3)*ФАКТР(5-D3)……………. Копируем эту формулу в ячейки F4,F5,F6,F7,F8.
Теперь вычислим (t-i)*Ci
G3=E3*F3…………..Копируем эту формулу в ячейки G4, G5, G6, G7, G8.
Теперь вычислим yi /((t-i)*Ci)
H3= B3/G3…………… Копируем эту формулу в ячейки H4, H5,H6,H7,H8.
Определяем П5+1 Е10=ПРОИЗВЕД(Е3:Е8)= -0,7024271.
Определяем :Е11= СУММ(Н3:Н8 = -1,858185.
Теперь непосредственно вычисляем f(0,1157)= П5+1* :Е12= Е10*Е11=1,30524.
Ответ: 1,30524.
Задания для самоконтроля.
Формула Лагранжа для неравноотстоящих значений аргумента.
А)
х |
у |
0,43 |
1,63597 |
0,48 |
1,73234 |
0,55 |
1,87686 |
0,62 |
2,03345 |
0,70 |
2,22846 |
0,75 |
2,35973 |
Вычислить значение функции f(x)=y(x) при x=0,512.
Б)
х |
у |
0,02 |
1,02316 |
0,08 |
1,09590 |
0,12 |
1,14725 |
0,17 |
1,21483 |
0,23 |
1,30120 |
0,30 |
1,40976 |
Вычислить значение функции f(x)=y(x) при x=0,203.
В)
х |
у |
0,35 |
2,73951 |
0,41 |
2,30080 |
0,47 |
1,96864 |
0,51 |
1,78776 |
0,56 |
1,59502 |
0,64 |
1,34310 |
Вычислить значение функции f(x)=y(x) при x=0,482.
Формула Лагранжа для равноотстоящих значений аргумента.
А)
х |
у |
1,375 |
5,04192 |
1,380 |
5,17744 |
1,385 |
5,32016 |
1,390 |
5,47069 |
1,395 |
5,62968 |
1,400 |
5,79788 |
Вычислить значение функции f(x)=y(x) при x=0,3926.
Б)
х |
у |
0,115 |
8,65729 |
0,120 |
8,29329 |
0,125 |
7,95829 |
0,130 |
7,64893 |
0,135 |
7,36235 |
0,140 |
7,09613 |
Вычислить значение функции f(x)=y(x) при x=0,1334.
В)
х |
у |
0,150 |
6,61659 |
0,155 |
6,39989 |
0,160 |
6,19658 |
0,165 |
6,00551 |
0,170 |
5,82558 |
0,175 |
5,65583 |
Вычислить значение функции f(x)=y(x) при x=0,1662.