
- •Рассмотрено на заседании пцк естественно-математических дисциплин
- •Пояснительная записка
- •Лабораторная работа №1 Тема: Элементарная теория погрешностей.
- •Лабораторная работа №2 Тема: Погрешности результата
- •Лабораторная работа №3. Тема: Отделение корней. Метод проб.
- •1. Метод Крамера.
- •2.Метод Гаусса.
- •3.Метод главных элементов.
- •4.Метод квадратных корней.
- •12. Метод итерации
- •13. Метод Зейделя
- •Лабораторная работа №12. Тема: Интерполирование функций.
- •Лабораторная работа № 13 Тема: Интерполирование функций.
- •1. Первая интерполяционная формула Гаусса.
- •2.Вторая интерполяционная формула Гаусса.
- •3. Интерполяционная формула Бесселя.
- •4. Интерполяционная формула Стирлинга.
- •Задания для самоконтроля.
- •Лабораторная работа №13. Тема: Интерполирование функций.
- •1. Первая интерполяционная формула Гаусса.
- •2.Вторая интерполяционная формула Гаусса.
- •3. Интерполяционная формула Бесселя.
- •4. Интерполяционная формула Стирлинга.
- •Задания для самоконтроля.
- •Лабораторная работа №14. Тема: интерполирование функций.
- •Задания для самоконтроля.
- •1)Заполните таблицу, используя следующие данные:
- •2)Заполните таблицу, используя следующие данные:
- •3)Заполните таблицу, используя следующие данные:
- •Лабораторная работа № 15. Тема: Симплекс-метод решения задач линейного программирования.
- •1. Введем зависимость для целевой функции:
- •2. Введем зависимости для левых частей ограничений задачи:
- •Задания для самоконтроля.
- •Лабораторная работа №16. Тема: Транспортная задача. Метод потенциалов.
- •1. Введём зависимость для целевой функции:
- •2. Введем формулу зависимости для целевой функции:
- •3. Введём зависимости для левых частей ограничений задачи:
- •Задания для самоконтроля.
Лабораторная работа №2 Тема: Погрешности результата
Задание 1:
Вычислить и определить погрешности результата
Х=![]() ,
где m=28.3(±2,02),n=7,45(±0,01),k=0,678(±0,003)
,
где m=28.3(±2,02),n=7,45(±0,01),k=0,678(±0,003)
Решение: для начала необходимо определить
m![]() ,n
,n![]() и
и
![]() .
Получаем:
.
Получаем:
m =(28,3) =800,9; n =(7,45) =413,5; =1,8234;
Далее определяем Х без учета абсолютных
погрешностей: Х=![]() =402,200
=402,200
Теперь определяем предельные относительные погрешности для m,n и k:
δ![]() =0,02/28,3=0,00071;
δ
=0,02/28,3=0,00071;
δ![]() =0,01/7,45=0,00134;
δ
=0,01/7,45=0,00134;
δ![]() =0,003/0,678=0,00442
=0,003/0,678=0,00442
Получив эти данные, определим погрешность результата:
δ![]() =2
δ
+3
δ
+0,5
δ
,
где 2 δ
т.к по условию дано m
,
3 δ
т.к. по условию дано n
,
0,5 δ
т.к. по условию дано k
=2
δ
+3
δ
+0,5
δ
,
где 2 δ
т.к по условию дано m
,
3 δ
т.к. по условию дано n
,
0,5 δ
т.к. по условию дано k![]()
Таким образом, δ =2 δ +3 δ +0,5 δ =2*0,00071+3*0,00135+0,5*0,00443=
=0,00142+0,00405+0,00222=0,00769=0,77%
В заключении определим предельную абсолютную погрешность результата:
∆ =Х* δ =402,200*0,0077=3,096994.
Ответ: Х=402,200(±3,097); δ =0,77%
Задание 2:
Вычислить и определить погрешности результата:
N=![]() ,
где n=3,0567(±0,0001), m=5,72(±0,02)
,
где n=3,0567(±0,0001), m=5,72(±0,02)
Для начала находим
n-1 =2,0567(±0,0001) (2,0567 получается из 3,0567-1),
m+n=5,72(±0,02)+3,0567(±0,0001)=8,7767(±0,0201),
m-n=5,72(±1,02)-3,0567(±0,0001)=2,6633(±0,0201) (погрешности складываются)
Далее определяем N без учета абсолютных погрешностей:
N=![]() =
=![]() =2,545≈2,55;
=2,545≈2,55;
Теперь определим предельные относительные погрешности для (n-1),(m+n) и (m-n) .
δ![]() =0,0001/2,0567=0,000049;
=0,0001/2,0567=0,000049;
δ![]() =1,0201/8,7767=0,0023;
=1,0201/8,7767=0,0023;
δ![]() =0,0201/2,6633=0,0075,
откуда определим погрешность результата:
=0,0201/2,6633=0,0075,
откуда определим погрешность результата:
δ![]() =
δ
+
δ
+ 2δ
,здесь
2δ
т.к. по условию дано (m-n)
=
δ
+
δ
+ 2δ
,здесь
2δ
т.к. по условию дано (m-n)
∆ = δ + δ +2δ =0,000049+0,0023+2*0,0075=0,0173=1,74%
В заключении определим предельную абсолютную погрешность результата:
∆ = N* δ =2,55*0,0173=0,044
Ответ: N ≈2,55(±0,044); δ =1,74%
Автоматический поиск погрешностей результата
Для автоматического поиска погрешностей результата начертите следующую таблицу в Excel т.к. показано на рис.2.1
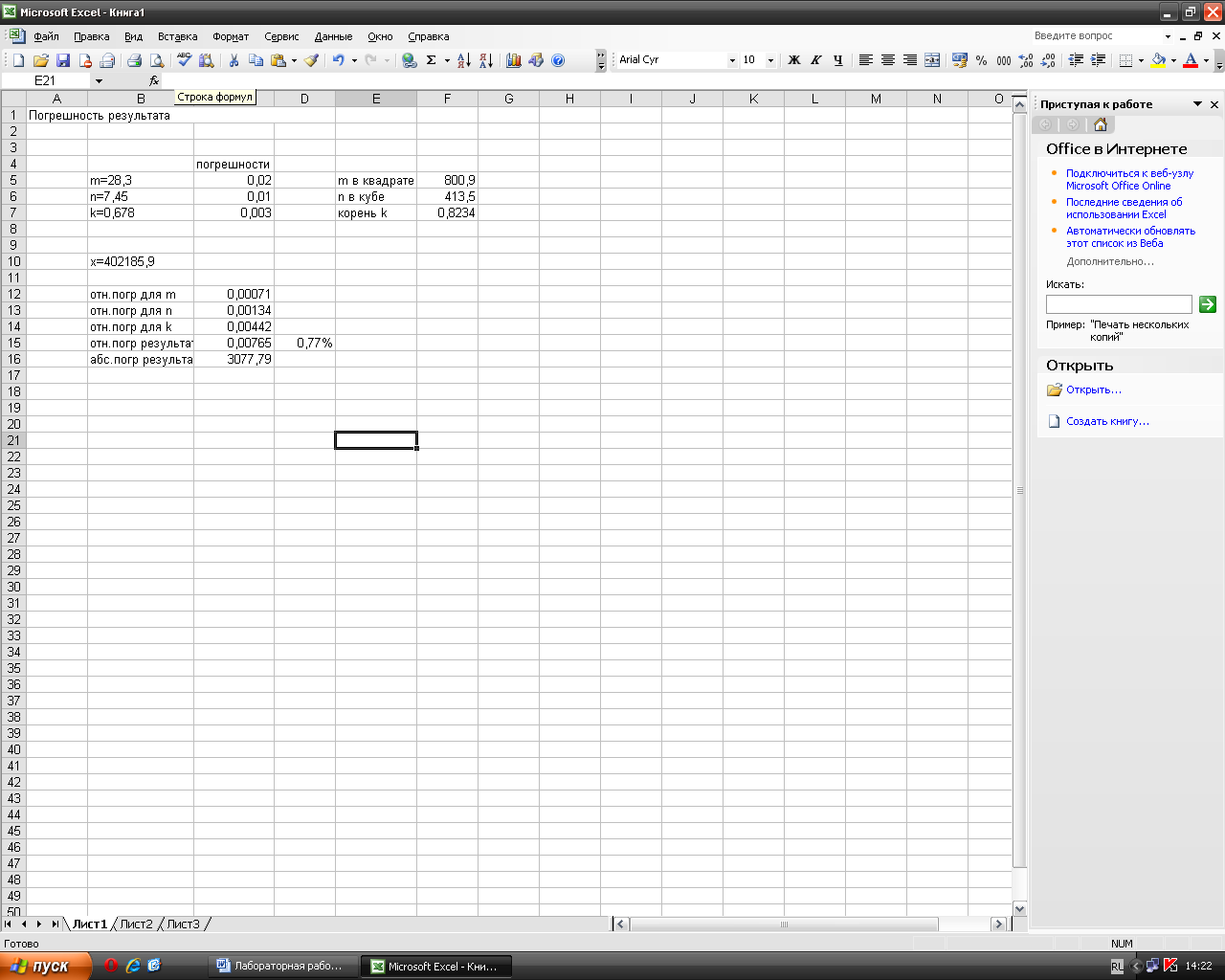
Рис.2.1. Автоматический поиск погрешностей результата
Определяем m :Ячейка F5=В5^2.
n : Ячейка F6=В6^3.
: Ячейка F7=КОРЕНЬ(В7).
Далее определяем X без учета абсолютных погрешностей: Ячейка В10= (F5*F6)/F7.
Теперь определим предельные относительные погрешности для
m: Ячейка С12=С5/В5.
n: Ячейка С13=С6/В6.
k: Ячейка С14=С7/В7.
Откуда определим погрешность результата
δ![]() :
Ячейка С15=2*С12+3*С13+0,5*С14.
:
Ячейка С15=2*С12+3*С13+0,5*С14.
В заключении определим предельную абсолютную погрешность результата ∆ : Ячейка С16=В10+С15.
Задания для самоконтроля: Определить какое равенство точнее:
а) X=
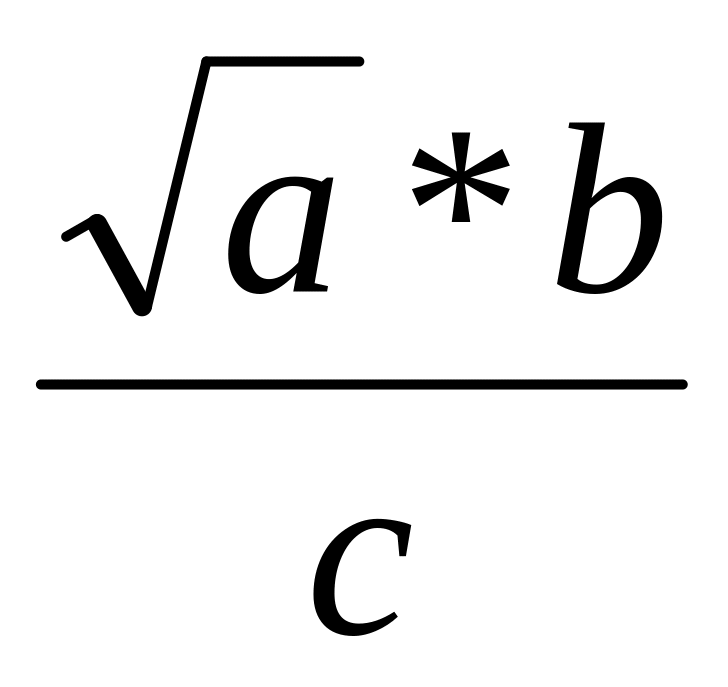 ,
a=228,6(±0,06),b=86,4(±0,02),c=68,7(±0,5).
,
a=228,6(±0,06),b=86,4(±0,02),c=68,7(±0,5).
Б) X=
![]() ,
m=4,22(±0,004),
a=13,5(±0,02),
b=3,7(±0,02),
c=34,5(±0,02),
d=23,725(±0,005)/
,
m=4,22(±0,004),
a=13,5(±0,02),
b=3,7(±0,02),
c=34,5(±0,02),
d=23,725(±0,005)/
2. а) X= , a=3,845(±0,04),b=16,2(±0,05),c=10,8(±0,1).
Б) X=
![]() ,
a=2,754(±0,001), b=11,7(±0,04), m=0,56(±0,005), c=10,536(±0,002),
d=6,32(±0,008).
,
a=2,754(±0,001), b=11,7(±0,04), m=0,56(±0,005), c=10,536(±0,002),
d=6,32(±0,008).
3. a) X=![]() ,
a=3,456(±0,002),b=0,642(±0,0005), c=7,12(±0,004).
,
a=3,456(±0,002),b=0,642(±0,0005), c=7,12(±0,004).
Б) X=![]() ,
a=23,16(±0,02), b=8,23(±0,005),
c=145,5(±0,08), d=28,6(±0,1),
m=0,28(±0,006).
,
a=23,16(±0,02), b=8,23(±0,005),
c=145,5(±0,08), d=28,6(±0,1),
m=0,28(±0,006).
Лабораторная работа №3. Тема: Отделение корней. Метод проб.
Задание 1. отделить корни аналитически
и уточнить один из них методом проб с
точностью до 0,01. х![]() -x
-2x
+3x-3=0
-x
-2x
+3x-3=0
Решение: Полагаем, что f(x)= х -x -2x +3x-3. Определим f(x), а затем найдем корни уравнения.
F(x) = х -x -2x +3x-3=0
4x(x -1)-3(x -1) =0
(x -1)(4x-3)=0
1) (x -1)=0 2) (4x-3)=0
x
= 1 x![]() =3/4
=3/4
x = -1
x = 1
Составим таблицу знаков функции f(x) (табл.3.1):
Таблица 3.1
Таблица знаков функции
x |
-∞ |
-1 |
3/4 |
1 |
+∞ |
Знак функции f(x) |
+ |
- |
- |
- |
+ |
Из таблицы видно, что уравнение имеет два действительных корня: x € [-∞;-1];x € [1;+∞]
Уменьшим промежутки, в которых находятся корни (табл. 3.2):
Таблица 3.2
Определение промежутков, содержащих корни уравнения
x |
-2 |
-1 |
1 |
2 |
Знак функции f(x) |
+ |
- |
- |
+ |
|
a
|
b
|
- |
+ |
Следовательно, x € [-2;-1];x € [1;2].
Уточним один из корней, например на промежутке [-2;-1], методом проб до сотых долей. Все вычисления удобно производить, используя следующую таблицу:
если в столбце f(x ) отрицательное число, то полученное число x =… заносится в столбец, где a или b отрицательны;
если в столбце f(x ) положительное число, то полученное число x =… заносится в столбец, где a или b положительны.
Знак a и b определяется из таблицы 3.2 знаков функции. В нашем случае a имеет знак “+”, т.е. a , а b имеет знак “-‘, т.е. b ).
Таблица 3.3
Таблица решения уравнения
N |
a |
b |
X
= |
f(x ) |
|a -b | |
0 |
-2 |
-1 |
-1,5 |
-3,5625 |
1 |
1 |
-2 |
-1,5 |
-1,750 |
0,3633 |
0,5 |
2 |
-1,750 |
-1,5 |
-1,625 |
-1,8923 |
0,25 |
3 |
-1,750 |
-1,625 |
-1,688 |
-0,8432 |
0,125 |
4 |
-1,750 |
-1,688 |
-1,719 |
-0,2555 |
0,062 |
5 |
-1,750 |
-1,719 |
-1,735 |
0,0488 |
0,031 |
6 |
-1,735 |
-1,719 |
-1,727 |
-0,0998 |
0,016 |
7 |
-1,735 |
-1,727 |
-1,731 |
-0,0208 |
0,008 |
Вычисляем до тех пор, пока |a -b |≤0.01
Ответ:х≈-1,73 (взяли меньшее)
Реализация этого метода в MS Exсel осуществляется следующим образом (Рис. 3.1)
Здесь вычисляемыми являются столбцы Н (т.е. х = ). I(т.е. f(х )), J(т.е. |a -b |)
H9=(F9+G9)/2 и аналогично для остальных a и b .
I9=H9^4- H9^3-2* H9^2+3* H9-3 и аналогично для остальных х
J9=ABC(F9-G9) и аналогично для остальных a и b .
Затем в зависимости от того является ли f(x ) положительным или торицательным числом, записываем x в a или в b
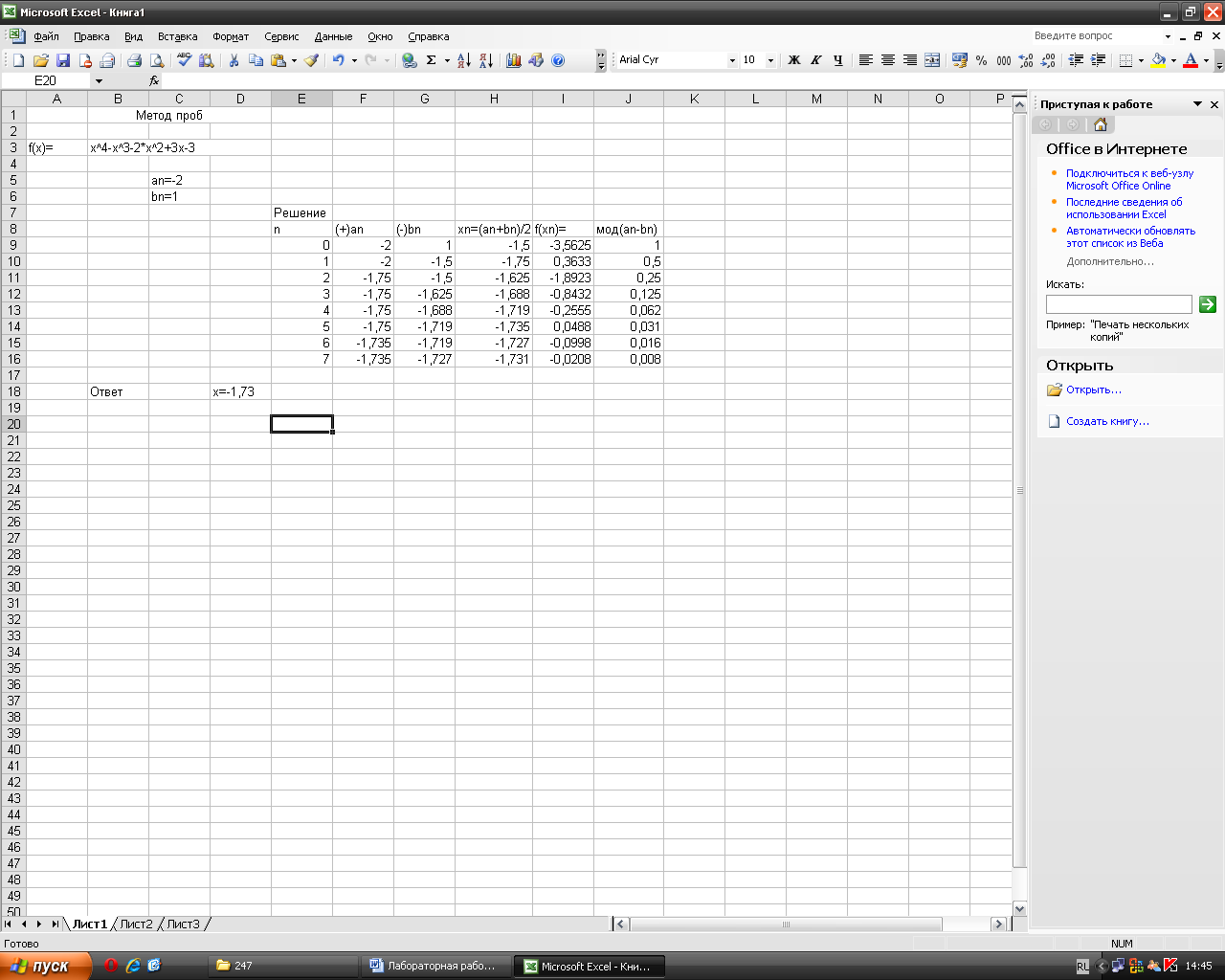
Рисунок 3.1
Задания для самоконтроля. Отделить корни аналитически и уточнить один из них методом проб с точностью до 0,01.
Вариант 1.
1. 2x -9x -60x+1=0;
2. 3x +8x +6x -10=0;
3. 3x -8x -18x +2=0.
Вариант 2.
2x +8x +8x -1=0;
x +4x -8x -17=0;
3x +4x -12x +1=0.
Лабораторная работа №4.
Тема: Отделение корней. Метод хорд.
Задание: Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до 0,001.
x -0,2x +0,5x+1,5=0
Решение: Полагаем, что f(x)= x -0,2x +0,5x+1,5. Определим f’(x), а затем найдем корни уравнения.
f’(x)=3x -0,4x+0,5=0
D=b -4ac=0,16-4*3*0,5=0,16-6= -5,84
D<0, следовательно непосредственно корни найти нельзя. Следовательно, необходимо найти интервал, в котором находятся корни данного уравнения f(x)=0. Возьмем любую точку, например, x=0 и будем перебирать все точки до тех пор, пока функция не изменит знак. И точки, в которых функция меняет знак, примем за границы интервала.
X |
-∞ |
-1 |
0 |
1 |
+∞ |
Sign f(x) |
- |
- |
+ |
+ |
+ |
Следовательно, уравнение имеет один действительный корень, лежащий в промежутке [-1;0].
Чтобы уточнить корень, находим вторую производную f’(x)=6х-0,4; в промежутке [-1;0] выполняется неравенство f”(x)<0. Подставляем интервал [-1;0] в функцию f”(x) и f(x) и находим при каком значении х знаки f”(x) и f(x) совпадают:
F”(-1)<0 f”(0)<0
f(-1)<0 f(0)<0
т.е. при х = -1 знаки f”(x) и f(x) совпадают
Следовательно, а = -1 – неподвижная точка
х![]() = 0 – подвижная точка
= 0 – подвижная точка
Для вычислений применяем формулу
х
![]() =
а -
=
а -
![]() *(x
-a)
*(x
-a)
Все вычисления располагаем в таблице:
N |
x |
x |
0 |
x =0 |
-0,882 |
1 |
x = -0,882 |
-0,943 |
2 |
x = -0,943 |
-0,946 |
3 |
x = -0,946 |
-0,946 |
x =0; f(0)=0-0+0+1,5=1,5
x =0
х
![]() =а
-
=а
-
![]() *(x
-a)=
-1-
*(x
-a)=
-1-
![]() *(0-(-1))=
-1-
*(0-(-1))=
-1-
![]() *(0+1)
= -0,882
*(0+1)
= -0,882
х
=а
-
![]() *(x
-a)=
-1 -
*(x
-a)=
-1 -
![]() *
(-0,882-(-1)) = -1-
*
(-0,882-(-1)) = -1-
![]() * 0,118= -0,943
* 0,118= -0,943
х
=а
-
![]() *(x
-a)=
-1 -
*(x
-a)=
-1 -
![]() *
(-0,943-(-1)) = -1-
*
(-0,943-(-1)) = -1-
![]() * 0,057 = -0,946
* 0,057 = -0,946
х![]() =а
-
=а
-
![]() *(x
-a)=
-1 -
*(x
-a)=
-1 -
![]() *
(-0,946-(-1)) = -1-
*
(-0,946-(-1)) = -1-
![]() * 0,054 = -0,946
* 0,054 = -0,946
|x![]() -x
|
= |-0,946-(-0,946)| = 0 ≤ 0,001
-x
|
= |-0,946-(-0,946)| = 0 ≤ 0,001
Вычисляем до тех пор, пока |x -x | ≤ 0,001
F(-0,882)=(-0,882) +0,2*(-0,882) +0,5*(-0,882)+1,5=-0,686-0,156-0,441+1,5=0,217
F(-0,943)=(-0,943) +0,2*(-0,943) +0,5*(-0,943)+1,5=-0,839-0,178-0,472+1,5=0,011
F(-0,946)=(-0,946) +0,2*(-0,946) +0,5*(-0,946)+1,5=-0,847-0,179-0,473+1,5=0,001
Ответ: x≈-0,946
Задания для самоконтроля: Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до 0,001
х -3х +6х+3=0;
х +0,2х +0,5х-2=0;
Задания для самостоятельной работы: Разработать требования к реализации этого метода в MS Excel
Лабораторная работа №5
Тема: Отделение корней. Метод касательных
Задание: Отделить корни уравнения аналитически и уточнить один из них методом касательных с точностью до 0,001
х -0,2х +0,5х-1,5=0;
Решение: Полагаем, что F(x)= х -0,2х +0,5х-1,5. Определим F’(x), а затем найдем корни уравнения
F’(x)= 3х -0,4х +0,4х+0,5=0
D=b -4ac=0.16-4*3*0.5=0.16-6= -5.84
D<0, поэтому непосредственно действительные корни найти нельзя. Следовательно, необходимо найти интервал, в котором находятся корни данного уравнения F(x)=0. Возьмем любую точку, например, х=0 и будем перебирать все точки до тех пор, пока функция не изменит знак. И точки, в которых функция меняет знак, примем за границы интервала.
X |
-∞ |
-1 |
0 |
1 |
+∞ |
Sign f(x) |
- |
- |
+ |
+ |
+ |
Следовательно, уравнение имеет один действительный корень, лежащий в промежутке [-1;0].
Чтобы уточнить корень, находим вторую производную f”=6x-0,4; в промежутке [-1;0]выполняется неравенство f”(х). Подставляем интервал [-1;0] в функции f”(х) и f(х) и находим при каком х знаки f”(х) и f(х) совпадают:
F”(-1)<0 f”(0)<0
f(-1)<0 f(0)<0
т.е.при х=-1 знаки f”(х) и f(х) совпадают
Следовательно, а=0 – неподвижная точка
х =-1 – подвижная точка
Т.е. в данном методе всё наоборот, чем в методе хорд
Для вычисления применяем формулу
х
=х
-![]()
Все вычисления располагаем в таблице: f(x) = 3x -0,4x+0,5
N |
х |
х |
0 |
-1 |
-0,949 |
1 |
-0,949 |
-0,946 |
2 |
-0,946 |
-0,946 |
x = -1
x
=x
-![]() =
-1-
=
-1-
![]() =
-1-
=
-1-
![]() =
-1+0,051= -0,949;
=
-1+0,051= -0,949;
x
=x
-![]() =
-0,949-
=
-0,949-
![]() =
-0,949-
=
-0,949-
![]() =
-0,949 + 0,003= -0,946;
=
-0,949 + 0,003= -0,946;
x
=x
-![]() =
-0,946-
=
-0,946-
![]() =
-0,946-
=
-0,946-
![]() =
-0,946-0,0002= -0,9458;
=
-0,946-0,0002= -0,9458;
|x
-x![]() |=|-0,9458-(-0,0946)|=0,0002≤0,001.
|=|-0,9458-(-0,0946)|=0,0002≤0,001.
Вычисляем до тех пор, пока |x -x |≤0,001.
F(-0,949)=(-0,949) -0,2*(-0,949) +0,5*(-0,949)+1,5= -0,855-0,180-0,475+1,5= -0,01;
f’(-0,949)=3* (-0,949) +0,4*(-0,949)+0,5=2,702+0,380+0,5=3,582;
F(-0,946)=(-0,946) -0,2*(-0,946) +0,5*(-0,946)+1,5= -0,847-0,179-0,473+1,5= 0,001;
f’(-0,946)=3* (-0,946) +0,4*(-0,946)+0,5=2,685+0,378+0,5=3,563.
Ответ: x≈ -0,946.
Задания для самоконтроля: Отделить корни уравнения аналитически и уточнить один из них методом касательных с точностью до 0,001
x -3x +6x+3=0;
x -0,2x +0,3x-1,2=0.
Задания для самостоятельной работы: Разработать требования к реализации этого метода в MS Excel.
Лабораторная работа №6.
Тема: Отделение корней. Комбинированный метод.
Задание: Комбинированным методом хорд и касательных решить уравнение третье степени, вычислив корни с точностью до 0,001.
x - 2x -4x+7=0.
Решение: Полагаем f(x)= x - 2x -4x+7=0. Определим f’(x)= 3x -4x-4=0.
Составим таблицу знаков функции для определения интервала, в котором лежат корни уравнения:
X |
-2 |
-1 |
0 |
1 |
2 |
3 |
Sign f(x) |
- |
+ |
+ |
+ |
- |
+ |
Т.е. корни уравнения находятся в интервалах [-2;-1],[1;2],[2;3].
Уточним корни уравнения комбинированным методом на одном из интервалов, например, на интервале [-2;-1]. Находим вторую производную f”(x)= 6x-4. Подставляем интервал [-2;-1] в функции f”(x) и f(x) и находим, при каком значении х знаки f”(x) и f(x) совпадают:
F”(-2)<0 f”(-1)>0
f(-2)<0 f(-1)<0
т.е. при х=-2 знаки f”(x) и f(x) совпадают.
Следовательно:
![]() =
-2, а х
=
-1.
=
-2, а х
=
-1.
Для расчетов применяем формулы:
x
=x
-
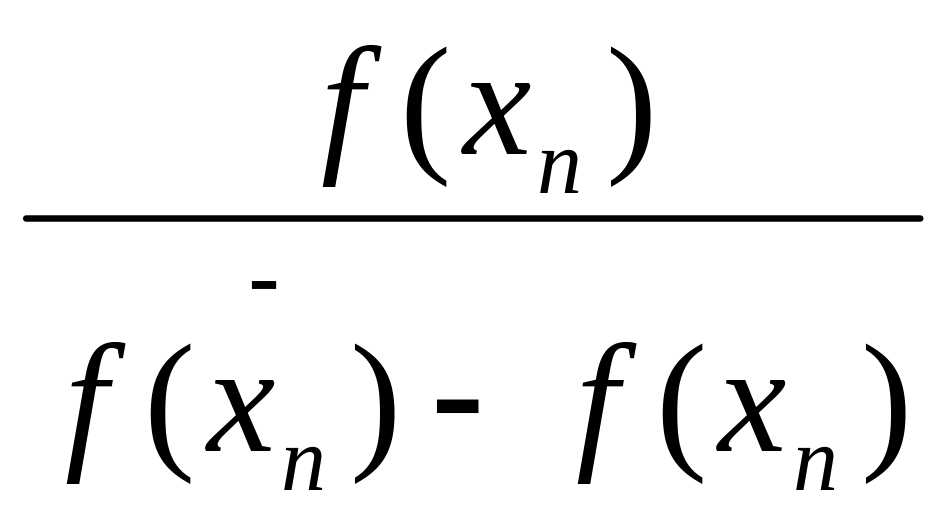 *(
*(![]() -x
);
-x
);
![]() =
=
![]() -
-
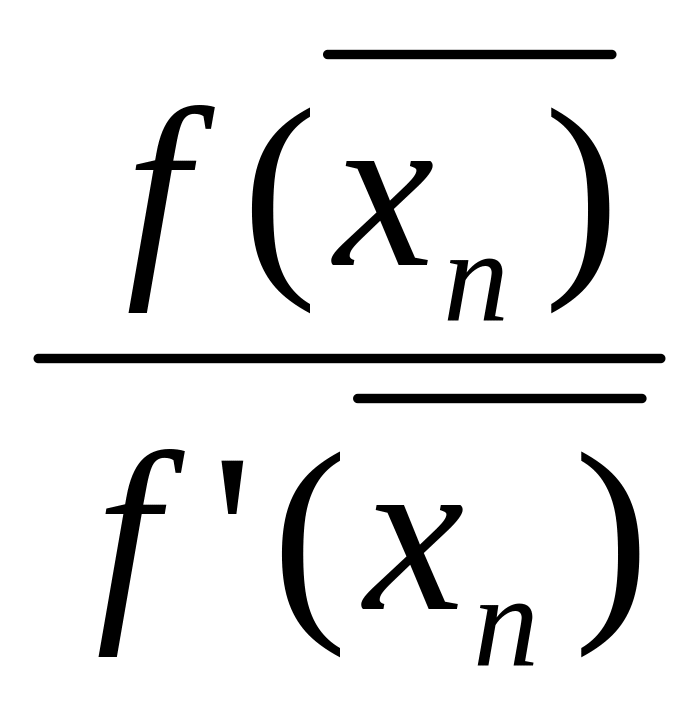 .
.
Все вычисления располагаем в таблице:
N |
x |
x |
|
|
|
0 |
-1 |
-1,889 |
-2 |
-1,938 |
|
1 |
-1,889 |
-1,9353 |
-1,938 |
-1,9354 |
Вычисляем до тех пор, пока | - x |≤0,001.
x = -1.
![]() =
-2.
=
-2.
x
=x
-
![]() *
(
-
x
)=
-1 -
*
(
-
x
)=
-1 -
![]() *(-1+2)=
-1,889.
*(-1+2)=
-1,889.
![]() =
-
=
-
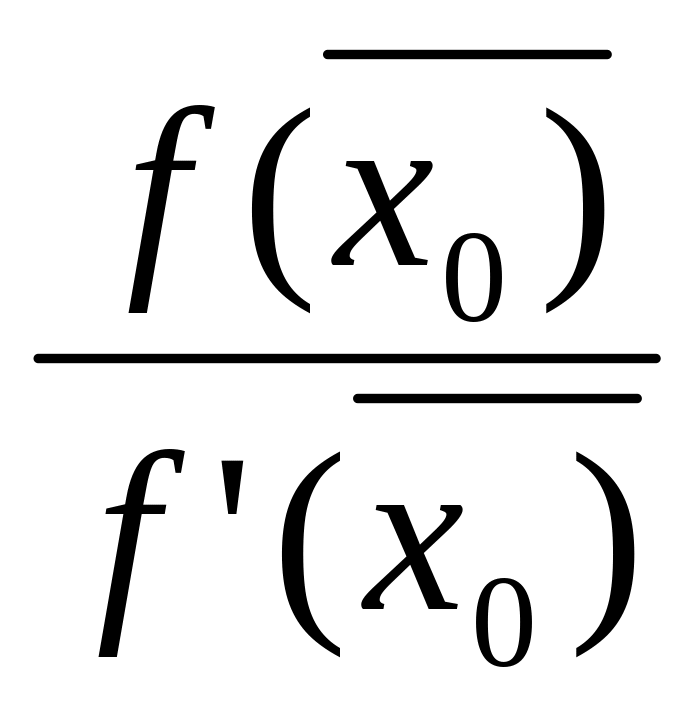 =
-2 -
=
-2 -
![]() =
-1,938.
=
-1,938.
f(x ) = f(-1)= -1-2+4+7= 8 f( )=f(-2)=-8-8+8+7= -1 f’( )=f(-2)=12+8-4=16
x
=x
-
![]() *
(
-
x
)
= -1,889-
*
(
-
x
)
= -1,889-
![]() *
(-1,938+1,889)= -1,9353.
*
(-1,938+1,889)= -1,9353.
![]() =
-
=
-
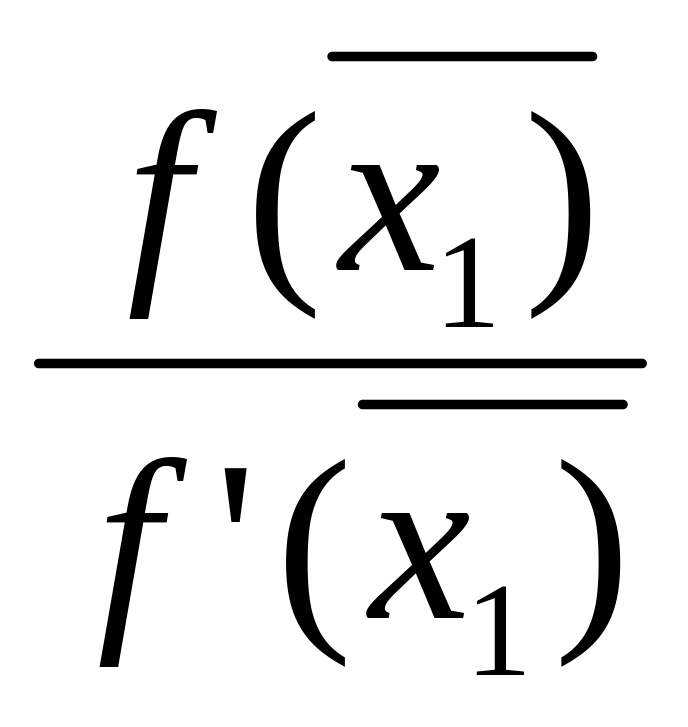 =
-1,938-
=
-1,938-
![]() =
-1,9354
=
-1,9354
f(x ) = f(-1,889)= -6,741-7,137+7,556+7=0,678 f( )=f(-1,938)=-7,279-7,512+7,752+7= -0,039
f( ) = f(-1,938) = 11,268+7,752-4= 15,02
| - x |= | -1,9354-(-1,9353)|=0,0001. Ответ: х ≈ -1,935.
Задания для самоконтроля:
x +4x -24x-10=0;
2x +9x -21=0.
Задания для самостоятельной работы: Разработать требования к реализации этого метода в MS Excel.
Лабораторная работа №7.
Тема: Отделение корней. Метод итерации.
Задание: Отделить корни уравнения аналитически и уточнить один из них методом итерации с точностью до 0,001.
x -2x +7x+3=0.
Решение: Полагаем f(x)= x -2x +7x+3=0. Составим таблицу знаков функции для определения интервала, в котором лежат корни уравнения:
X |
-2 |
-1 |
0 |
1 |
2 |
Sign f(x) |
- |
- |
+ |
+ |
+ |
Т.е. корни уравнения находятся в интервалах [-1;0].
Уточним этот корень методом итерации. Для этого приведём функцию к виду x= φ(x), где | φ(x)|<1.
Находим f’(x)=3x -4x+7.
f’(-1)=3+4+7=14 f’(0)=0-0+7=7.
Q =max| f’(x)|= max(14 и 7)=14.
Определяем k=10. (берем меньшее ближайшее удобное число к 14)
φ(x)= х -
 ;
φ(x)= х -
;
φ(x)= х -
 +
+
 -
-
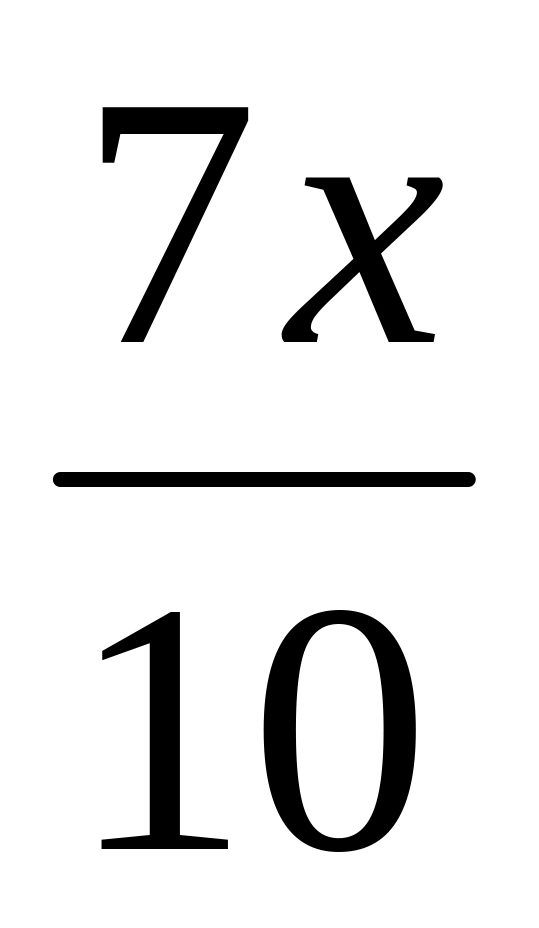 -
-
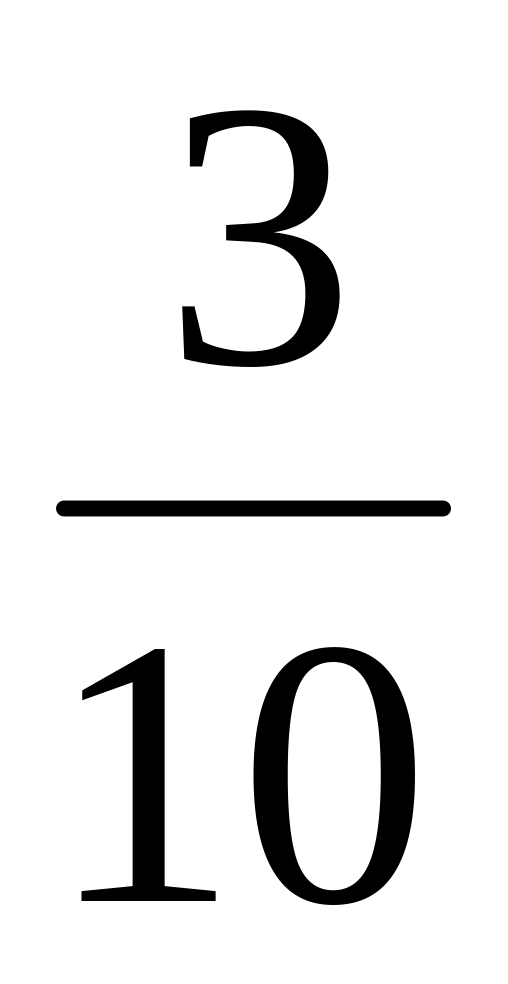 = х -0,1х
+0,2х
-0,7х-0,3
= х -0,1х
+0,2х
-0,7х-0,3φ(x)= -0,1х +0,2х -0,3х-0,3.
Пусть х =0, тогда х = φ(x ). Все вычисления располагаем в таблице:
-
N
х
φ(x )
0
0
-0,3
1
-0,3
-0,3693
2
-0,3693
-0,3784
3
-0,3784
-0,3795
4
-0,3795
-0,3796
5
-0,3796
Вычисляем до тех пор, пока |x -x |≤0,001.
F(0)= -0,3;
f(-0,3)= 0,0027+0,018-0,09-0,3= -0,3693;
f(-0,3693)= 0,0050+0,0273-0,1107-0,3= -0,3784;
f(-0,3784)= 0,0054+0,0286-0,1135-0,3= -0,3795;
f(-0,3795)= 0,0055+0,0288-0,1139-0,3= -0,3796;
|x -x |= |-0,3796-(-0,3795)|=0,001.
Ответ: х ≈ -0,3796.
Задания для самоконтроля: Отделить корни уравнения аналитически и уточнить один из них методом итерации с точностью до 0,001.
x -3x +9x-10=0;
x +0,4x +2,6x-1,6=0;
x +3x +12x+3=0;
2x +0,2x +0,5x +0,8=0.
Лабораторная работа №8.
Тема: Решение систем линейных уравнений.
