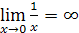Тема 3. Функция и ее свойства.
В данной теме необходимо знать некоторые определения, ведущие к выполнению заданий на:
1) нахождение области определения функции
2) нахождение множества значений ее
3) определение четности или нечетности
4) определение ее ограниченности
5) определение промежутков монотонности функции.
Определения.
1. Переменная y называется функцией переменной x , если каждому допустимому значению x соответствует определенное значение y и записывается в виде y=f(x), где символ f означает совокупность действий над х, чтобы получить значение у.
2. Областью определения функции называется множество всех действительных значений х, при которых выполняются все операции, заложенные формулой этой функции y=f(x).
3. Множеством значений функции называется множество всех действительных значений функции у, которые она может принимать.
4. Функция называется четной в области ее определения, если выполняется равенство
f(-x)=f(x) и нечетной, если выполняется равенство f(-x)=-f(x)
График четной функции симметричен относительно оси ОУ, график нечетной функции симметричен относительно начала прямоугольной системы координат.
5. Функция y=f(x) называется ограниченной в области ее определения, если найдется такое число М>О, что выполняется неравенство │f(x)│≤М. В противном случае она называется неограниченной.
6. Функция y=f(x)называется возрастающей, если для х1<х2 взятых из области определения ее выполняется неравенство f(x1)<f(x2) и убывающей, если при x1<x2 выполняется неравенство f(x1)>f(x2). Возрастающие и убывающие функции называются монотонными.
Тема 4. Понятие предела функции в точке. Теоремы о пределах.
Необходимо понимать, что пределом функции y=f(x) в точке хо является некоторое число А, которое должно удовлетворять некоторому условию для этой функции y=f(x). Условие это задается важнейшим определением:
Число
А называется пределом функции f(x)
в точке хо
и обозначается
=A,
если для любого числа 
найдется такое число 
такое, что для всех x,
удовлетворяющих неравенству 
-
где, х≠х0,
выполняется неравенство А-
<f(x)<A+
.
Графическая иллюстрация
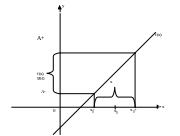
Для вычисления пределов используют специальные теоремы и следствие из них.
Теорема 1. Предел суммы функций f(x) и g(х) равен сумме пределов этих функций, т.е.
Теорема
2. Предел произведения функций 
(x)
и 
(х)
равен произведению пределов этих
функций, т.е.
Теорема 3. Предел частного функции (x) и (х) равен частному пределов этих функций, т.е.
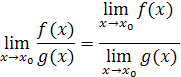
Следствия из теорем:
1. Постоянный множитель к можно вынести за знак предела, т.е.
2. Предел целой рациональной функции
F(x)=a0xn+a1xn-1+a2xn-2+an-1x+an
в точке x0 равен значению этой функции в этой точке, т.е.
Теоремы имеют смысл только в том случае, если существуют пределы функций f(x) и y(x) в точке х0.
Для вычисления пределов необходимо запомнить два замечательных предела:
Первый
второй
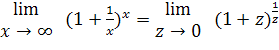=e
Так же для вычисления пределов надо знать два равенства о пределах связанных с понятиями бесконечно малой и бесконечно большой величины.
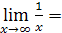0
и 2)
