
- •Кафедра общеобразовательных дисциплин математика
- •Специальность 030912 Право и организация социального обеспечения
- •Оглавление
- •Пояснительная записка
- •Объем дисциплины и виды учебных занятий
- •Тематический план
- •Программа курса
- •Тема 1. Действительные числа. Приближенные вычисления
- •Тема 2. Функции. Свойства и графики функций. Предел функции
- •Тема 3. Тригонометрические функции. Тригонометрические уравнения
- •Тема 4. Прямые, плоскости и углы в пространстве
- •Тема 5. Показательная, степенная, логарифмическая функции.
- •Тема 6. Многогранники. Объемы и площади поверхностей многогранников
- •Тема 7. Производная и ее применение
- •Тема 8. Первообразная, интеграл
- •Тема 9. Тела вращения. Объемы и площади поверхностей тел вращения
- •Тема 10. Координаты и векторы в пространстве
- •Тема 11. Элементы комбинаторики, статистики и теории вероятностей
- •Методические рекомендации по изучению дисциплины.
- •Тема 1. Иррациональные неравенства с одной переменной.
- •Тема 2. Системы двух нелинейных уравнений с двумя неизвестными.
- •Тема 3. Функция и ее свойства.
- •Тема 4. Понятие предела функции в точке. Теоремы о пределах.
- •Тема 5. Тригонометрические формулы одного аргумента.
- •Тема 6. Формулы сложения двух аргументов, формулы удвоенного аргумента.
- •Тема 7. Тригонометрические уравнения.
- •Тема 8. Степень. Показательные уравнения и неравенства.
- •Тема 9. Логарифмы. Логарифмические уравнения и неравенства.
- •Тема 10. Производная функция и ее применение.
- •Тема 11. Первообразная и интеграл.
- •Методические рекомендации по организации самостоятельной работы студентов
- •Тема: Системы двух линейных уравнений с двумя неизвестными. Определитель третьего порядка.
- •Тема. Понятие функции область определения и множество её значений. Чётность и нечётность функции, и её ограниченность.
- •Тема. Вычисление пределов функций.
- •Тема. Тригонометрические формулы единого аргумента.
- •Тема Тригонометрические уравнения.
- •Тема. Показательные уравнения, их виды и способы решения. Показательные неравенства, их виды и способы решения.
- •Тема. Логарифмы. Логарифмические уравнения и неравенства.
- •Тема. Производная. Применение производной к исследованию функции и построениям графика.
- •Тема. Наибольшее и наименьшее значение функции
- •Тема. Первообразная функции. Неопределенный интеграл.
- •Тема определённый интеграл.
- •Тема. Элементы комбинаторики и теории вероятности
- •Примеры контрольных заданий для проведения рубежного контроля
- •1 Семестр
- •2 Семестр
- •Тематика рефератов
- •Рекомендуемая литература Основная
- •Дополнительная
- •Задания для выполнения зачетной контрольной работы
- •I вариант
- •II вариант
- •III вариант
- •IV вариант
- •Вопросы для подготовки к экзамену
2 Семестр
ВАРИАНТ 1.1
Даны векторы
|
b
|
|
Н айти длину вектора d = 2a – 3b + c
Составить уравнение прямой, проходящей через точку А (-2;-7) и образующей с осью ОХ угол 60
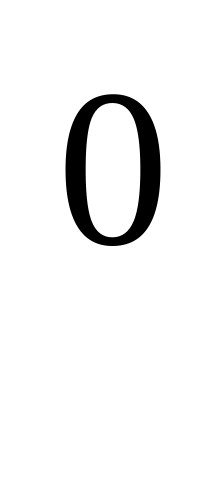 .
.
Найти координаты центра и радиус окружности х
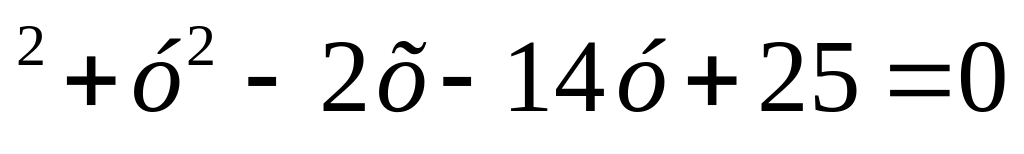 .
.
Точки А и В лежат в плоскости , а точка С не лежит в этой плоскости. Доказать, что прямая, проходящая через середины отрезков АС и ВС параллельна плоскости .
Наклонная АМ = 10 см, проведенная из точки А к данной плоскости, образует с этой плоскостью угол 45 . Найти проекцию наклонной.
ВАРИАНТ 1.2
Даны векторы
m = 2i + 3j
|
n = -2i + j
|
p = -i + 2j
|
Н айти длину вектора k = -3m + 2n - p
Составить уравнение прямой, проходящей через точку B (2;-6) и образующей с осью ОХ угол 45 .
Составить уравнение окружности концы диаметра АВ которого имеют координаты А (-2;3) и В (2;5).
Точка М не лежит в плоскости прямоугольника АВСД. Доказать, что прямая СД параллельна плоскости АВМ.
Наклонная, равная 20 см, образует с данной плоскостью угол 60 . Найти длину проекции этой наклонной на эту плоскость.
ВАРИАНТ 1.3
Даны векторы
d
|
e = -i + 3j
|
f = 4 j
|
Н айти длину вектора q = -d + 4e – 2f
Составить уравнение прямой, образующей угол 30 с осью ОХ угол 45 и проходящей через точку С (-1;9).
Составить уравнение окружности с центром в точке S (-1;4) и проходящей через точку М (3;5).
Точка Q не лежит в плоскости трапеции MNPK с основаниями MK и NP. Доказать, что прямая МК параллельна плоскости NQP.
Наклонная, равная 30 см, образует с плоскостью угол 30 . Найти длину проекции этой наклонной на эту плоскость.
ВАРИАНТ 1.4
Даны векторы
к = 8i
|
|
s = 2i - 3j
|
Н айти длину вектора e = k – 2r –3s
Составить уравнение прямой, образующей с осью ОХ угол arctg (-5) и проходящий через точку Д (3;8).
Найти уравнение окружности, проходящей через начало координат с центром в точке S (-2;3).
Точка N не лежит в плоскости параллелограмма EFHP. Доказать, что прямая ЕР параллельна плоскости FNH.
Под углом
 к
плоскости
проведена
наклонная. Найти этот угол
,
если проекция наклонной вдвое меньше
самой наклонной.
к
плоскости
проведена
наклонная. Найти этот угол
,
если проекция наклонной вдвое меньше
самой наклонной.
ВАРИАНТ 2.1
Даны точки А(-2;4), В(3;-6), С(4;-2), Д(1;5). Вычислить скалярное произведение векторов
А В
и СД.
В
и СД.
Составить уравнение сторон треугольника с вершинами А (-3;-2), В (1;5) и С (8;-4).
Составить уравнение эллипса, если две его вершины находятся в точках (-5;0) и (5;0), а фокусы в точках (-3;0) и (3;0).
В кубе АВСDA
 B
C
D
построить сечение плоскостью, проходящей
через вершины B
и
C
и точку М – середину ребра ДС.
B
C
D
построить сечение плоскостью, проходящей
через вершины B
и
C
и точку М – середину ребра ДС.
Внутри двугранного угла в 120 дана точка М, равноудаленная от каждой грани на расстоянии 4 см. Найти расстояние от этой точки М до ребра двугранного угла.
В АРИАНТ
2.2
АРИАНТ
2.2
Найти угол между векторами АВ и СД, если А (3;1), В (7;4), С (3;2) и Д (6;6).
Вершины треугольника заданы точками М (-1;-3), N (3;5) и P (4;0). Найти уравнения его сторон.
Составить уравнение эллипса, если расстояние между фокусами 10 (фокусы лежат на оси ОХ) и большая ось равна 12.
В кубе АВСDA B C D построить сечение плоскостью, проходящей через вершины А и Д и точку К, ГД середина ребра D C .
В тетраэдре ДАВС все ребра равны, точка М – середина ребра АС. Доказать, что
 -
линейный для двугранного угла ВАСД.
-
линейный для двугранного угла ВАСД.
ВАРИАНТ 2.3
Найти косинус угла между векторами а + в и а – в, если а = (2;3) и в = (1;1).
Треугольник DEF задан вершинами D (-3;4); E (-4;-3) и F (8;1). Определить уравнения всех трех его сторон.
Составить уравнение эллипса, фокусы которого находятся в точках (-4;0) и (4;0), а эксцентриситет е = 0,8.
В кубе АВСDA B C D построить сечение плоскостью, проходящей через вершины B и C и точку Р – середину АA .
Гипотенуза прямоугольного треугольника лежит в плоскости , а катет наклонен к этой плоскости под углом в 30 . Найти угол между плоскостью и плоскостью треугольника.
В АРИАНТ 2.4
К акому условию должны удовлетворить векторы а и в, чтобы вектор а + в был перпендикулярен вектору а – в.
Даны координаты вершин треугольника Н (2;5), Р (-6;-4) и К(6;-3). Каковы уравнения всех трех его сторон?
Найти координаты вершин эллипса, длины его осей и эксцентриситет, если эллипс имеет уравнение
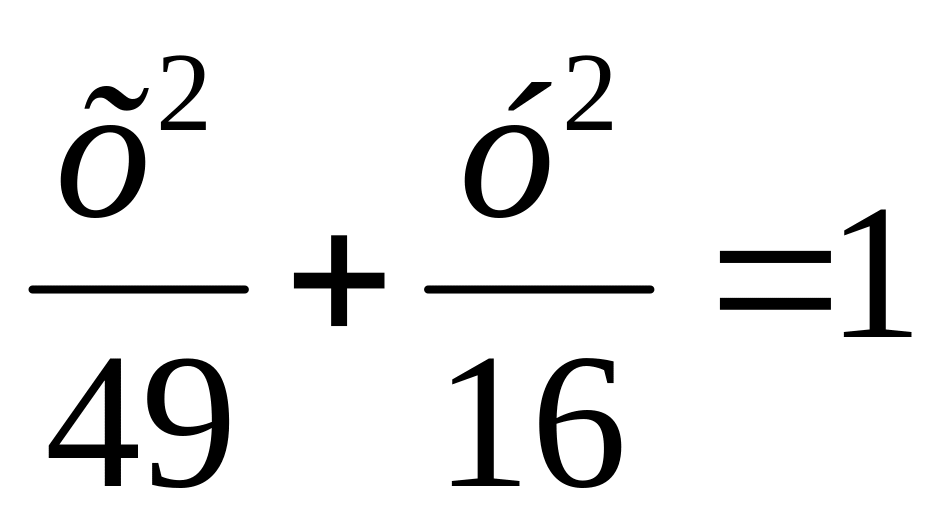 .
.
В кубе АВСDA B C D построить сечение плоскостью, проходящей через вершины A и B и точку L, где L – середина ребра АD.
На грани двугранного угла в 60 дана точка, удаленная от ребра на расстоянии 10 см. найти расстояние от этой точки до другой грани.
ВАРИАНТ 3.1
Расстояние от точки М, лежащей на оси ОХ до точки N (10;5) равно 13. Найти точку М.
Найти вершины ∆АВС, если его стороны АВ, АС и ВС заданы уравнениями: х + 3у – 3 = 0, 3х – 11у – 29 = 0 и 3х – у + 11 = 0
Даны прямые 2х – 3у + 6 = 0 и 3х – у – 3 = 0. Найти острый угол между ними.
Составить уравнение гиперболы, если её вершины находятся в точках А (-3;0) и А (3;0), а фокусы в точках F (-5;0) и F (5;0).
Через точку О пересечения диагоналей квадрата MNPQ проведена прямая ОК так, что КМ=КР и KN=KQ. Доказать, что ОК перпендикулярна плоскости квадрата.
ВАРИАНТ 3.2
Расстояние от точки В, лежащей на оси ОУ, до точки А (3;-1) равно 5. Найти точку В.
Вычислить координаты вершин MNP, если 4х + 3у +20 = 0, 6х – 7у – 16 = 0 и х –5 у + 5 = 0 уравнения сторон MN, NP, MP.
Вычислить угол между прямыми
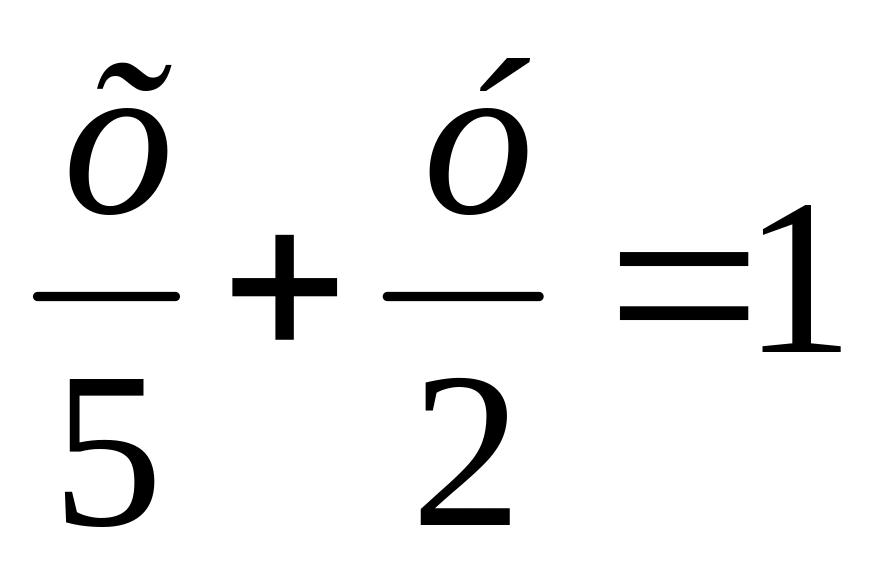 и
и
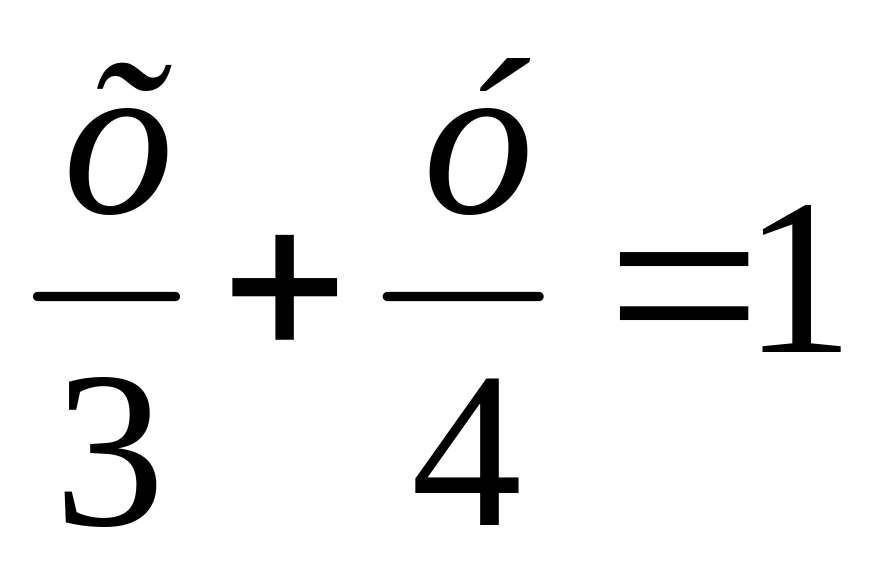 .
.Найти уравнение гиперболы с фокусами на оси ОХ, если длина её действительной оси равна 12, а расстояние между фокусами равно 20.
Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая ОМ так, что АМ=МС и МВ=МD. Доказать перпендикулярность прямой ОМ к плоскости параллелограмма.
ВАРИАНТ 3.3
Вычислить координаты точки на оси ОХ, равноудаленной от точек А(5;13) и В (-12;-4).
Стороны ∆CDE заданы уравнением 7х + 3у – 25=0, 2х – 7у – 15=0 и 9х – 4у + 15 = 0. Определить координаты вершин C, D и E
Две прямые заданы уравнениями 5х – 12у – 16 = 0 и 3х + 4у – 12=0. Найти угол между ними.
По уравнению гиперболы
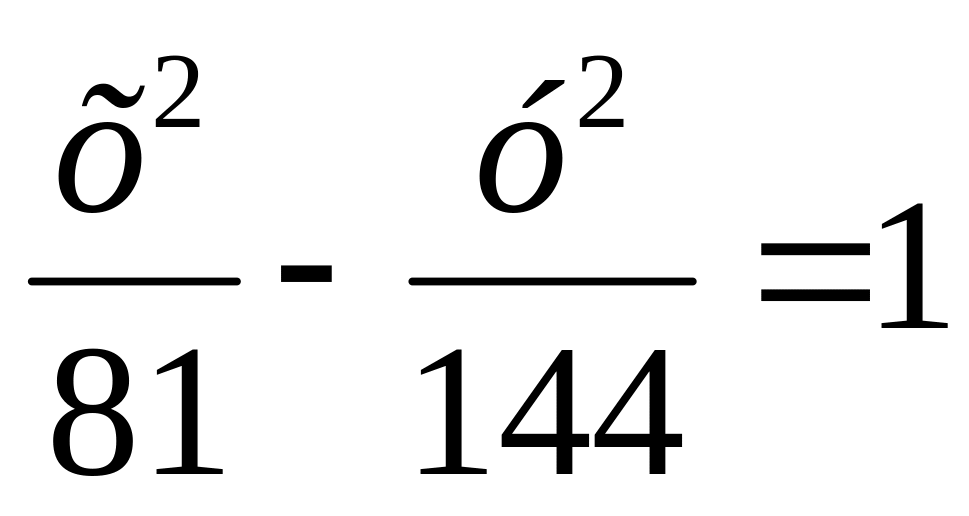 вычислить
координаты её вершин и фокусов.
вычислить
координаты её вершин и фокусов.
Через точку О пересечения диагоналей ромба MNKP проведена прямая OS так, что SM = SК и SN=SP. Доказать, что прямая OS перпендикулярна плоскости ромба MNKP.
ВАРИАНТ 3.4
Вычислить координаты точки на оси ОУ, равноудаленной от точек М(-4 ;0) и N (-3;-7).
Определить координаты вершин ∆QRS, стороны которого заданы уравнениями 5х - 3у – 15=0, х + 5у – 3=0 и 3х + у + 5 = 0.
Какова величина угла между прямыми 3х+4у-12 = 0 и 15х - 8у – 45=0.
Определить уравнения асимптот гиперболы по уравнению самой гиперболы
Прямая АМ перпендикулярна к плоскости квадрата АВСД, диагонали которого пересекаются в точке О. Доказать, что прямая ВД перпендикулярна к плоскости АМО.
ВАРИАНТ 4.1
Вычислить координаты точки С – середины отрезка АВ, если А(-1;2) и В(5;-4).
Составить уравнение прямой, проходящей через точку М(-2;4), параллельно прямой 2х – 3у + 6 = 0
В кубе АВСDA B C D найти угол между скрещивающимися прямыми АА и B D.
По уравнению параболы у = 6х составить уравнение её директрисы.
Из точки А к плоскости L проведены перпендикуляр и наклонная, угол между которыми равен 30◦. Найти наклонную и её проекцию на данную плоскость, если перпендикуляр равен 2 см.
ВАРИАНТ 4.2
Точка К делит отрезок MN в отношении 3:5 (от M к N), где М (2;3) и N(10;11). Найти точку К.
Параллельно прямой
 через
точку А (-1;-4) проходит другая прямая.
Найти её уравнение.
через
точку А (-1;-4) проходит другая прямая.
Найти её уравнение.
В кубе MNPQM N P Q вычислить угол между скрещивающимися отрезками N P и QQ
По данному уравнению параболы у = - 4х вычислить координаты её фокуса.
Из точки М к плоскости проведены перпендикуляр и наклонная, образующие угол 60 . Найти длину перпендикуляра и проекции наклонной, если сама наклонная равна 4 .
ВАРИАНТ 4.3
Найти координаты точки Д, которая делит отрезок PF в отношении 1:3 (от F к P), если Р (-3;-2) и F (9;6).
Параллельны ли прямые 3х – 2у +5 = 0 и 4у – 6х – 7 = 0 и какая из них проходит через точку S (-1; 1).
В кубе EFYHE F Y H определить величину угла между скрещивающимися прямыми EY и FF .
Составить уравнение параболы с вершиной в начале прямоугольной системы координат, если фокус находится в точке F (3;0).
Если наклонные раны, то равны их проекции. Доказать.
ВАРИАНТ 4.4
Отрезок DH, концами которого служат точки D (3;-2) и H (10;-9) делится точкой Е в отношении 2:5. Найти точку Е.
Через точку Н (2;-9) проходит прямая, параллельная прямой -5х + 4у – 8 = 0. Составить уравнение этой прямой.
В кубе ABCDA B C D найти величину угла между скрещивающимися прямыми A C и DD .
Составить уравнение параболы с вершиной в начале прямоугольной системы координат, если директрисой её служит прямая х = 4.
Доказать, что если проекции наклонных равны, то равны и сами наклонные.
ВАРИАНТ 5.1
Найти угловой коэффициент прямой 3у – 4х + 5 = 0 и угол, образованный этой прямой с осью ОХ.
Составить уравнение прямой, проходящей через точку М (2;3), перпендикулярно прямой 5х – 4у – 20 = 0.
Дано: А а, а
 .
Доказать: А
.
.
Доказать: А
.
Диагональ куба равна 3. Найти расстояние от вершины куба до плоскости диагональю сечения.
Внутри двугранного угла в 120 дана точка М, равноудаленная от каждой грани на расстоянии 4 см. Найти расстояние от этой точки М до ребра двугранного угла.
ВАРИАНТ 5.2
Дана прямая 2х – 6у + 7 = 0. вычислить её угловой коэффициент и угол образованный этой же прямой с осью ОХ.
Составить уравнение прямой, перпендикулярной прямой
 и проходящей через точку М (-4;1).
и проходящей через точку М (-4;1).
Дано: А
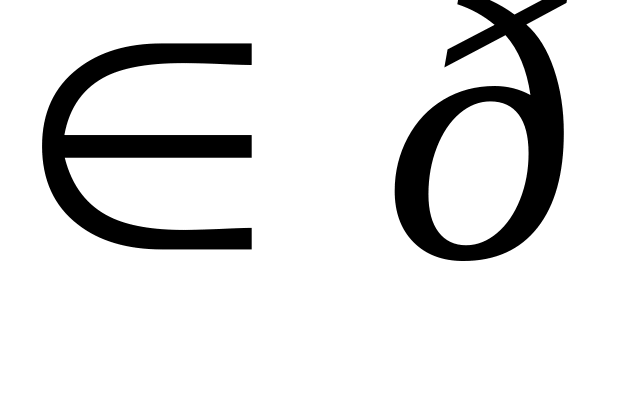 ,
В
,
А
,
В
,
А
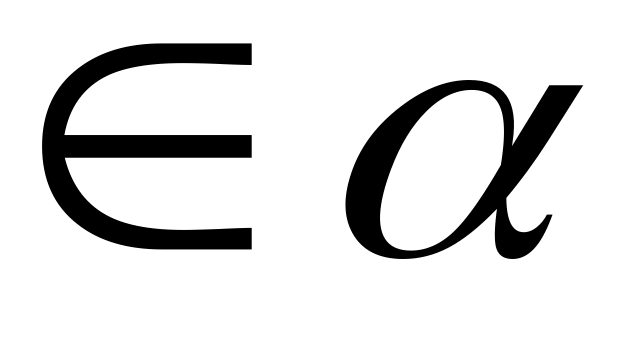 ,
В
.
Доказать р
.
,
В
.
Доказать р
.
Один конец отрезка лежит в плоскости , а другой находится от неё на расстоянии 6 см. Найти расстояние от середины данного отрезка до плоскости .
В тетраэдре ДАВС все ребра равны. Точка М – середина ребра АС. Доказать, что
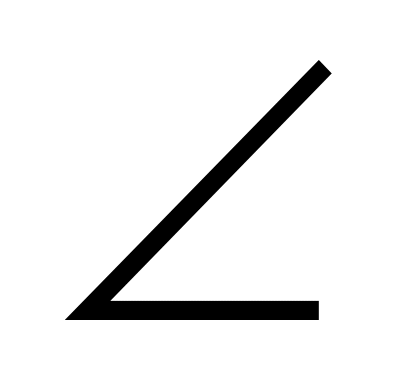 ДМВ
– линейный для двугранного угла ВАСД.
ДМВ
– линейный для двугранного угла ВАСД.
ВАРИАНТ 5.3
Определить угловой коэффициент прямой – 8у + 6х – 1 = 0 и угол, образованной этой прямой с осью ОХ.
Найти уравнение прямой, проходящей через начало прямоугольной системы координат, перпендикулярно прямой 2х + 3у – 12 = 0.
Дано: А , В , р . Доказать: А , В .
Концы отрезка отстоят от плоскости на расстоянии 1 см и 4 см. Найти расстояние от средины данного отрезка до плоскости .
Гипотенуза прямоугольного треугольника лежит в плоскости , а катеты наклонены к этой плоскости под углом в 30 . Найти угол между плоскостью и плоскостью треугольника.
ВАРИАНТ 5.4
Вычислить угловой коэффициент прямой 10х + 5у – 2 = 0 и угол, образованный этой прямой с осью ОХ.
Определить уравнение прямой, проходящей через центр окружности (х+2) + (у-5) =1 перпендикулярно прямой 5х – 2у + 10 = 0.
Дано: А , А
 .Доказать:
А
.
.Доказать:
А
.
Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см. найти расстояние от точки М до плоскости АВС, если АВ = 6см.
На грани двугранного угла в 60 дана точка, удаленная от ребра на расстоянии 10 см. Найти расстояние от этой точки до другой грани.

 а
= -2i
– 3j
а
= -2i
– 3j = 5i
= 5i
 c
= 3i – 5j
c
= 3i – 5j
 =
5i -
j
=
5i -
j

 r = 7j
r = 7j