Тема определённый интеграл.

Неопределённый интеграл становится определённым, если известны пределы интегрирования а и в. Определённый интеграл имеет вид

, где а – нижний предел интегрирования, в- верхний предел интегрирования.

Определённый интеграл рассчитывается по формуле Ньютона-Лейбница.

Способы интегрирования те же самые, т.е. способ непосредственного

интегрирования и способ замены переменной.

Определённые интегралы обладают теми же свойствами, что и не определённые

интегралы.

Задание 1. Вычислить интеграл непосредственным интегрированием.

Пример 1.

Алгоритм решения

1. Находим первообразную F(x)для функции f(x)= .

2. В данном интеграле а=-2 и в=1. Поэтому вычисляем F(в)=F(1), а затем F(а)=F(-2).

3. Находим разность F(в)- F(а)= F(1)- F(-2).

Решение

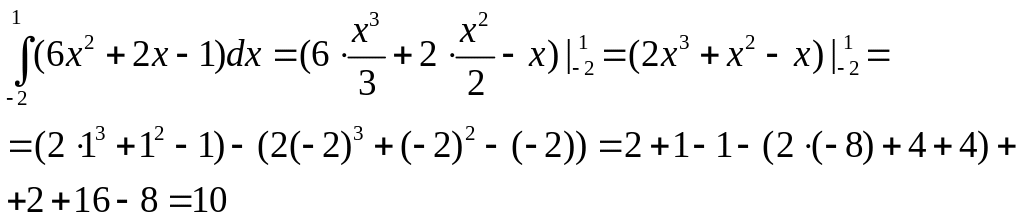
Ответ: 10.

Пример 2. Решение по прежнему алгоритму.

Решение

Пример 3. Используем формулу lV из таблицы параграфа 62, стр. 264.

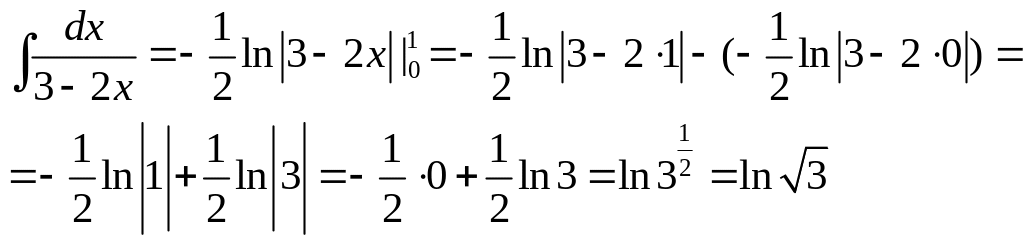
Ответ

Пример 4.

1. Сначала преобразуем , используя (а-в) (а+в)=

Решение: затем ещё раз будем использовать разность квадратов.

Замена:

Ответ: -8464.

Геометрический смысл определённого интеграла заключается в том, что

есть число, выражающее площадь фигуры, ограниченной линиями х=а, х=в, у=0 и у=f(х) и осью ОХ, т.е. площадь некоторой фигуры.

Задание 2. Вычислить площадь фигуры, ограниченной данными линиями х=а, х=в, у=0 и у=f(х).

Пример 1. фигура ограничена линиями у=х², х=0, х=в, х=-2 и у=0. Найти площадь.

Решение:

1. Строим указанные линии в прямоугольной системе координат: три прямые и одну

центральную параболу.

2. Выделяем фигуру.

3. Применяем формулу Ньютона-Лейбница.

4. Ответ.

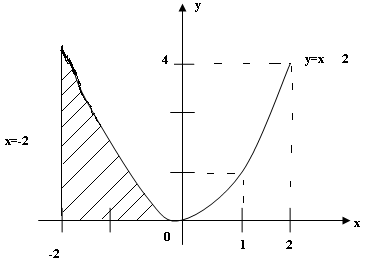
Пример 2. Вычислить площадь фигуры, ограниченной линиями

Решение:

Приравниваем у=0, т.е. решаем уравнение . - точки пересечения параболы с осью ОХ.

Вершина имеет координаты (0; 9), т.к. х=0

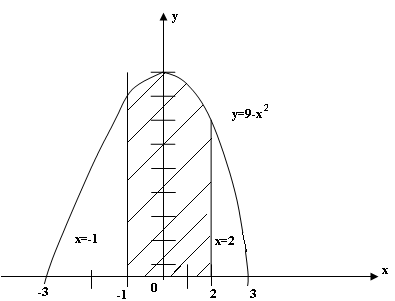
Ответ Sфиг =

Рекомендуемая литература по теме:

1. Математика: учебник для ссузов / Н.В. Богомолов - М: Дрофа, 2005 г.,

66 стр. 271

2. Практические занятия по математике: учебное пособие для техникумов

/ Богомолов Н. В. - М.: Высшая школа, 1979 г (гл. 11 1, 2; гл 12 1).

3. Алгебра и начала анализа: Дидактические материалы для 10-11 класса / Шабунин

М. И. - М.: Мнемозина, 1998 г., 33, 34, 35

4. Сборник задач по математике: учебное пособие для ссузов / Н. В. Богомолов –

М.: Дрофа, 2006 г. 39 стр. 62, 80 упр. № 673 стр. 132-133

Тема. Элементы комбинаторики и теории вероятности

В теме «комбинаторика» студент обязан знать определение трёх видов соединений и

уметь вычислять их, применяя к условию задач с использованием соответствующих

формул.

Справочный материал:

1. Размещение из n элементов по m:

2. Перестановки из n элементов:

или !

3. Сочетания из элементов по m:

n!=1 2 3 4…n,

m!= 1 2 3 4…m.

Основные виды упражнений в теме:

1. Вычисление или упрощение выражения, содержащее эти соединения.

2. Решение уравнений и систем уравнений содержащие .

3. Решение текстовых задач с использованием указанных соединений.