Тема. Производная. Применение производной к исследованию функции и построениям графика.
Для понимания этой темы справочным материалом будут:
1.формулы и правила дифференцирования
2.критерии монотонности функции
3.критерии выпуклости графика функции
4.критерии экстремумов функции
5.Общая схема исследований функций
Общая смеха исследований функций :но которой находят:
1.Область определяет y=f(x)
2.Производную функции f(x)
3.Стационарные точки функции f(x)
4.Промежутки монотонности функции
5.Эктремумы функции
6.Промежутки выгнутости и вогнутости графика
7. Для более точного построения графика дополнительно можно найти точки пересечения с осями ,определить четность(или нечетность ее,и вычислить координаты нескольких контрольных точек.
Задание: исследовать и функции и построить ее график.
Пример:
Решение:
1.Область
определения функций есть множество
всех действительных чисел,
R,т.к.
при них выполняются все операции
,заложенные в формуле функции.
2.Находятся f(x):
3.Решаем уравнения
:
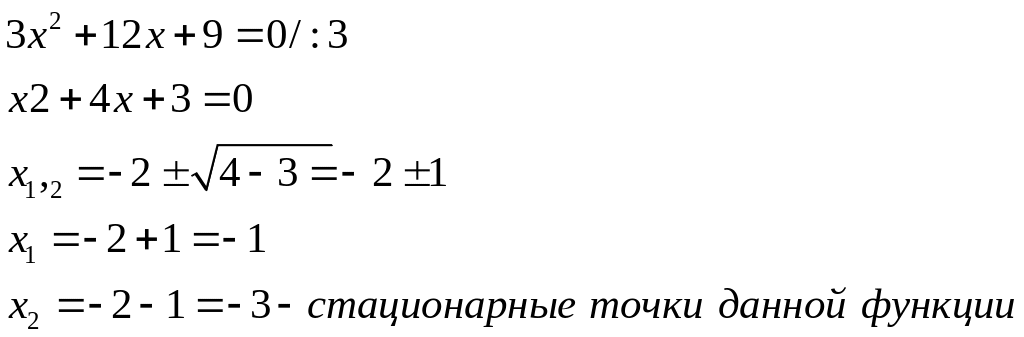
4.Промежутки монотонности определим с помощью интервалов ,построенных на основе стационарных точек. Делаем рисунок.
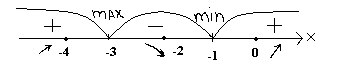
В
каждом из интервалов находим знак
производной, т.е. f
или
(x)=
для чего в эту функцию х подставили
внутреннею точку каждого интервала.
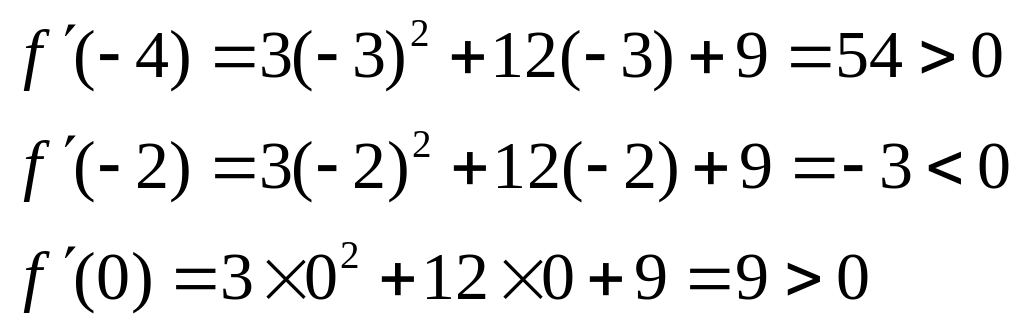
Т.к. f(x) меняет знак + на – при переходе х=-3, то х=-3-точка максимума.
Т.к. f(x) меняет знак с- на+ при переходе через х=-1,то точка х=-1-точка максимума.
Следовательно при х<-3 и х>-1 функция возрастает ,а при -3<х<-1 функция убывает.
5.Вычислить экстремумы функции f(x)
f
max=f(-3)=
,т.е.
имеем точку графика (-3;8)
f
min=f(-1)=
имеем
точку графика (-4;1).
6.Для
вычисления промежутков и точек изгиба
находим вторую производную f(x)
являющеюся для производной
для
.
Составляем ур-ние f(x)=0 и решаем его:
6х+12=0/:6
Х+2=0
Х=-2-критическая точка второго рода .Она делит числовую прямую на интервалы, в каждом из которых определяется второй знак производной.
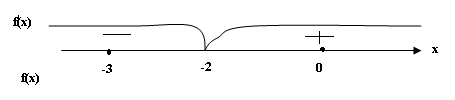
(-3)=
и график выпуклый вверх
график
выпуклый вниз
Т.к.
при переходе через х=-2 вторая производная
меняет знак, то сама точка х=-2 является
точкой перегиба. Вычислим её,
,
т.е. имеет точку (-2;6)
7. Найдём контрольные точки графика:
1) при х=0 f(0)=8 и точка будет (0;8)
2) при х=1 f(1)=1+6+9+8=24 и точка будет (1;24)
3)
при х=-4 f(-4)=
и точка будет (-4; 4).
Построение графика осуществляется в прямоугольной системе координат с помощью всех найденных точек.
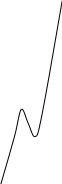
Тема. Наибольшее и наименьшее значение функции
Справочный материал
Если
функция y=(x)
непрерывна на некотором промежутке
значений х (
),то
для вычисления наибольшего и наименьшего
значений её необходимо пользовать
следующим алгоритмом:
1.Найти
производную функцию
.
2.Вычислить критические (стационарные) точки функции из уравнения =0
3.В тех критических точках, которые принадлежат промежутку [a; в],
вычислить значение данной функции f(x)
4.Вычислить значение данной функции f(x) на концах промежутка, т.е. f(a) и f(в)
5. Сравнить полученные числа.
Большее из них будет набольшим значением функции f(x) но [а; в] и обозначатся max f(x), а меньшее число – наименьшим значением функции f(x) [а,в] и записывается min f(x).
Задание. Найти наибольшее и наименьшее значение функции f(x) на данном значении функции [а, в].
Пример 1.
f(x)=
Решение ведём по алгоритму:
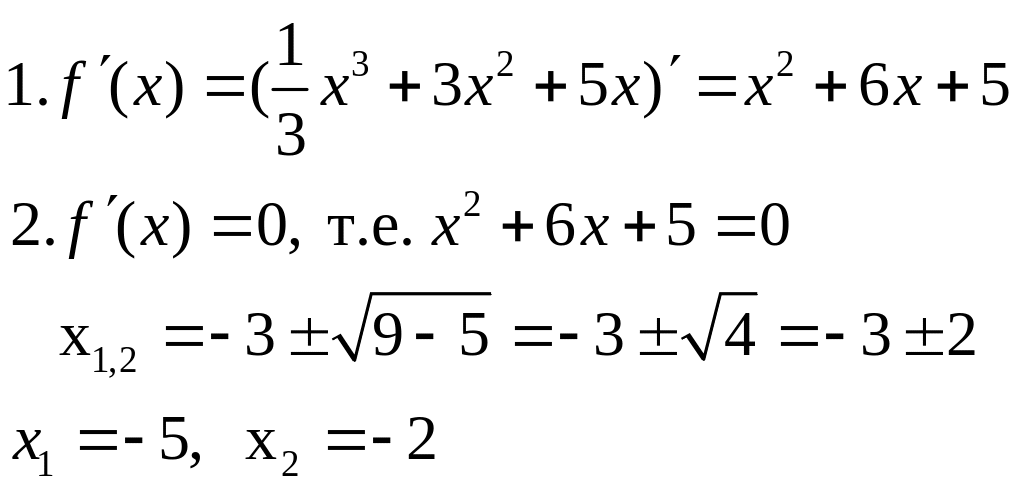
Критические точки функции f(x).
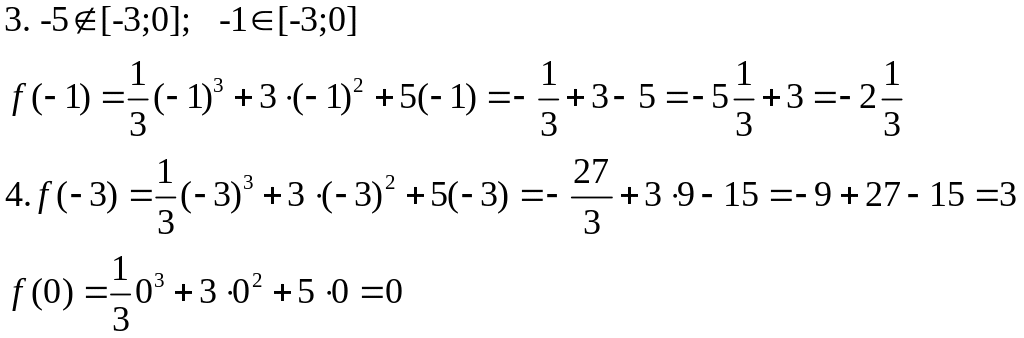
5.
Получили числа:
,
3, 0.
Ответ
f(x)
= f(-3)=3;
f(x)=f(-1)=
.
Пример 2.
Решение
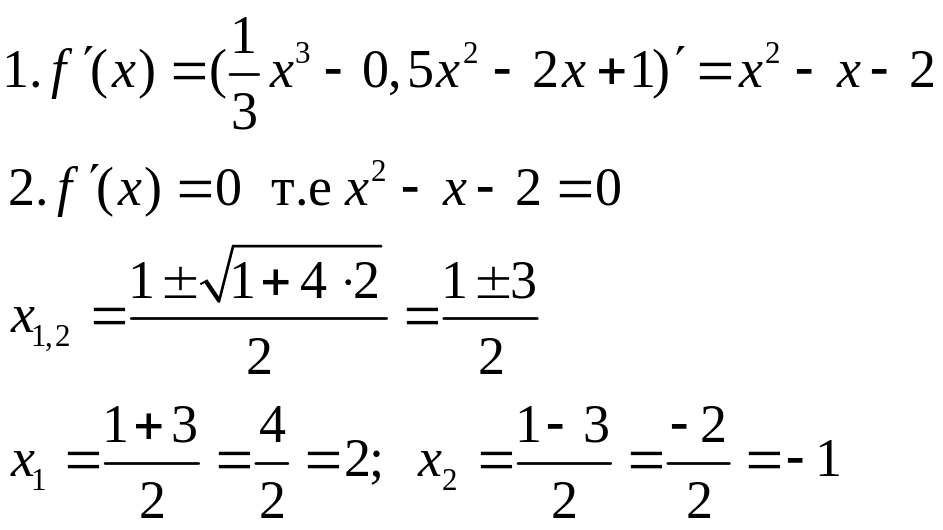
критические точки функции f(x).
3.2
[3;4]
; -1
[3;4]
Ни одна точка не принадлежит данному промежутку. Поэтому
вычисляем значения функции f(x) только на концах промежутка.
4.
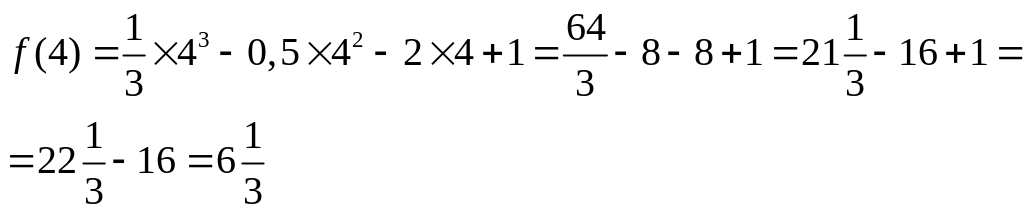
Получим
два числа -0,5 и
Ответ:
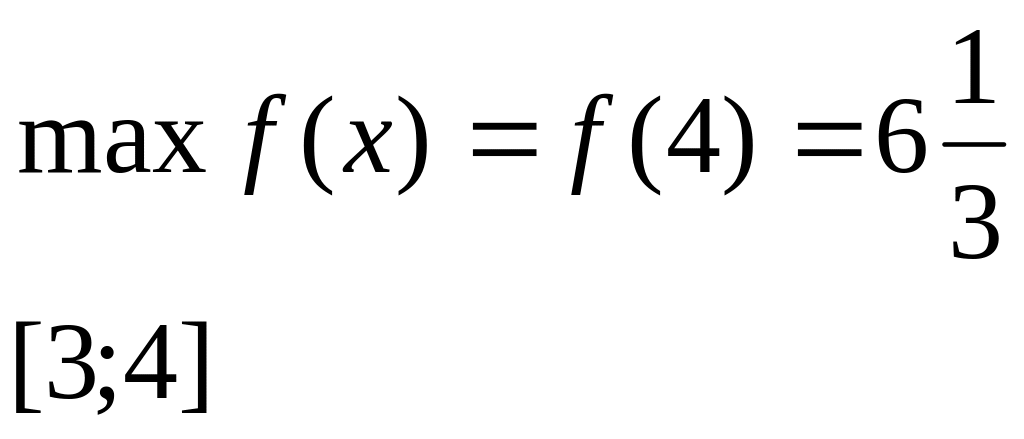
Рекомендуемая литература:
1. Математика: учебник для ссузов / Н.В. Богомолов - М: Дрофа, 2005 г., 56 п.5
2. Практические занятия по математике: учебное пособие для техникумов
/ Богомолов Н. В. - М.: Высшая школа, 1979 г (гл. 7 4).
3. Алгебра и начала анализа: Дидактические материалы для 10-11 класса / Шабунин
М. И. - М.: Мнемозина, 1998 г., 30
4. Сборник задач по математике: учебное пособие для ссузов / Н. В. Богомолов –
М.: Дрофа, 2006 г.