Тема. Вычисление пределов функций.

Задание. Вычислить пределы.

Пример 1.

Решение.

По следствию из теории о пределах необходимо подставить вместо х число -2.

Получили:

Пример 2.

Решение:

По следствию из теоремы о пределах х получили

Пример 3.

Решение:

Подставим в функцию вместо х число -5.

В таком случае неопределённости вида необходимо числитель и знаменатель разложить на множители.

Выполним разложение квадратного трёхчлена по формуле корни уравнения 0.

Составим уравнения.

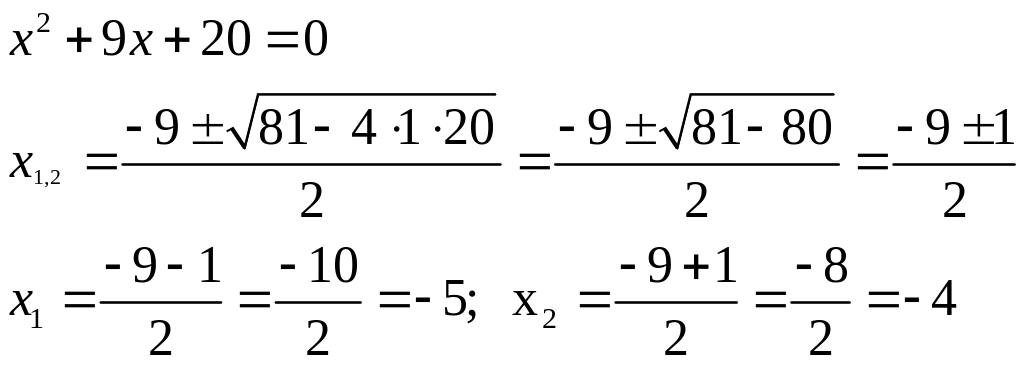
Следовательно (х+5)(х+4)

Аналогично для знаменателя:

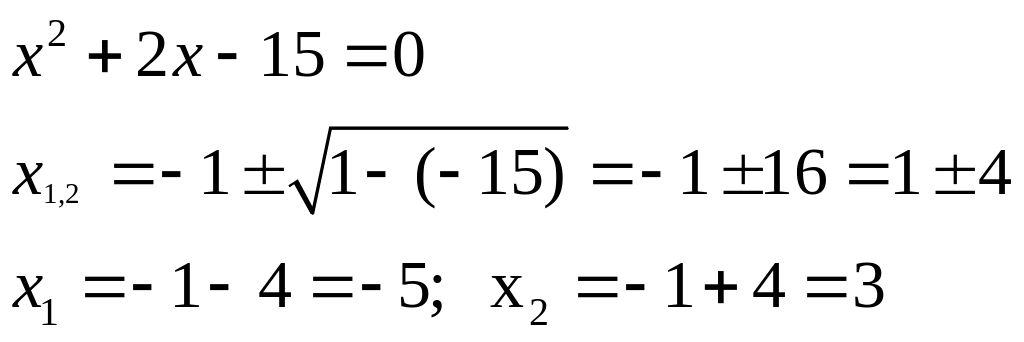
Тогда (х+5)(х-3)

Теперь вычислим данный предел:

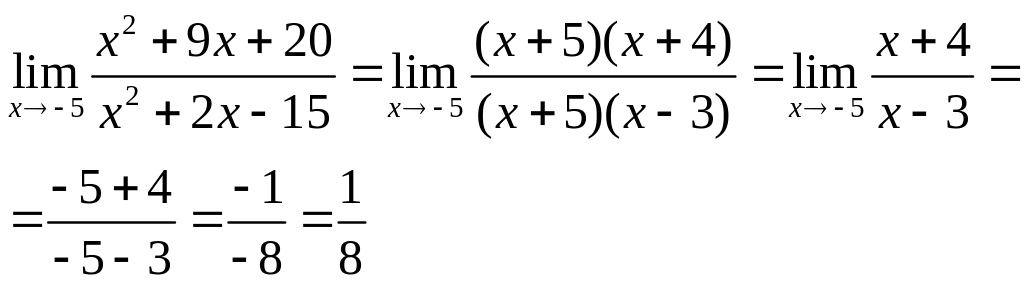
Пример 4.

Решение:

Подставим вместо х число 4 в функцию.

Полученную неопределённость раскрываем через разложение на множители числителя.: .

Тогда:

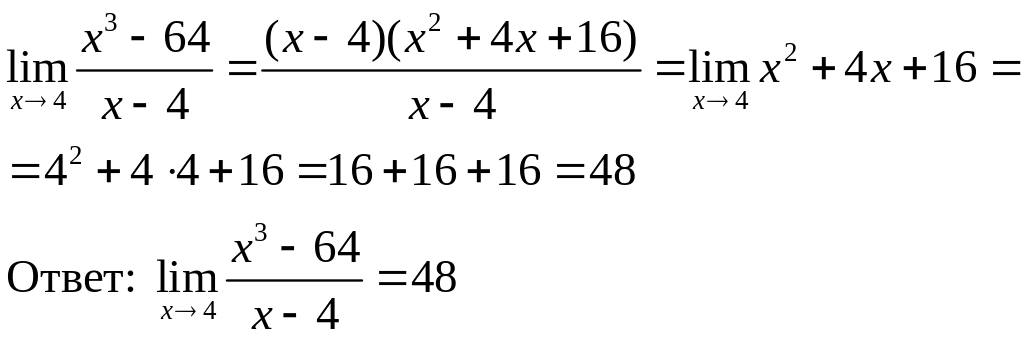
Пример 5.

Подстановка вместо х символа даёт неопределенность вида

В этом случае необходимо числитель и знаменатель поделить на высшую степень х, т.е. на х²

Решение:

Делим числитель, и знаменатель на с учётом правила деления

алгебраической суммы на число.

Получили

Учитывая равенство , и применяя теоремы и следствия о пределах, будем иметь:

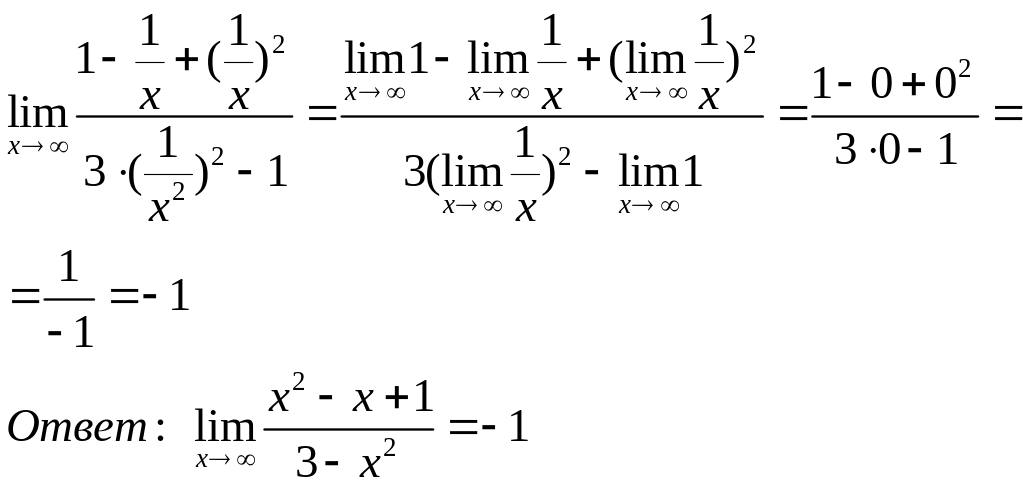
Пример 6.

, решение и его стандартное оформление

Пример 7.

Решение

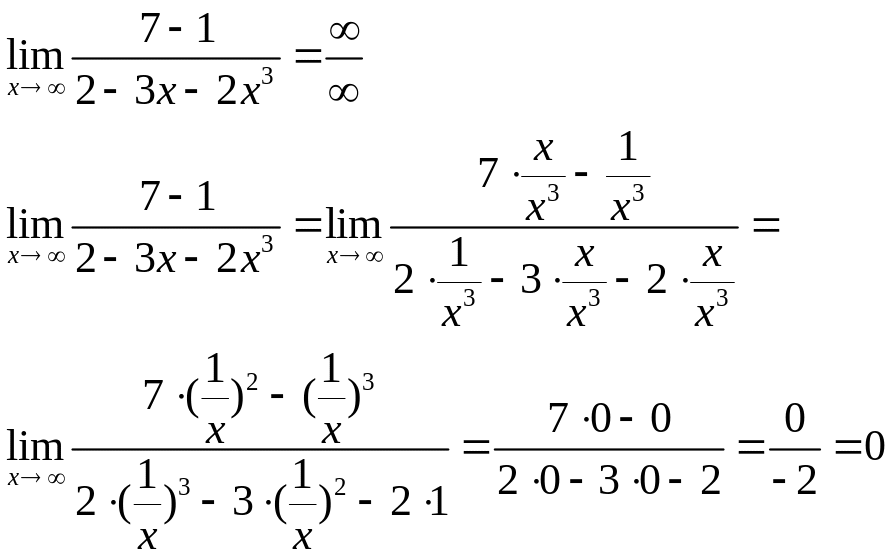
Ответ: = 0

Примечание. Студент должен понимать, что 0 - это символ бесконечно-малой величины, очень близкой к нулю, но не «чистый» 0. Поэтому выражение имеет смысл.

При изучении этой темы обращайтесь к следующей литературе:

1.Математика: учебники для вузов (Н.В. Богомолов). 43 п. 1 , стр. 202

2.Практикум по математике под реакцией Н. В. Богомолова.

Тема. Тригонометрические формулы единого аргумента.

Все формулы тригонометрии одного аргумента происходят из основного тригонометрического тождества и определений и.

Рассмотрим решения главных видов упражнений по этому вопросу.

Задание 1.

Вычислить:

Решение:

Необходимо по одной данной своим числовым значением тригонометрической функции вычислить все остальные.

Оформление решения.

Дано: Найти

1) 2)Т.к. угол по условию лежит в 3 четверти, в которой ,то 3) .

Ответ:

Задание 2.

Упростить выражение

В решении таких заданий надо уметь сочетать формулы тригонометрии с формулами сокращенного умножения.

В нашем примере используем сумму кубов:

Тогда получим: =

Ответ:1

Пример 2:

Используем квадрат разности и ,а так же то, что .

Получим:

Ответ

Задание 3. Доказать тригонометрическое тождество.

Студенты знакомы с такими видами заданий из школы и должны помнить, что бы доказать тождество, надо доказать равенство обеих частей его. В тригонометрии при этом используют весь арсенал тригонометрических формул совместно с формулами сокращённого умножения.

Пример 1.

Преобразуем правую часть равенства и докажем, что она равна левой части, т.е.1, вынося общий множитель в левой части .

Пример 2.

Как только в тригонометрическом выражении присутствуют вместе с целесообразно заменить

Получим решение:

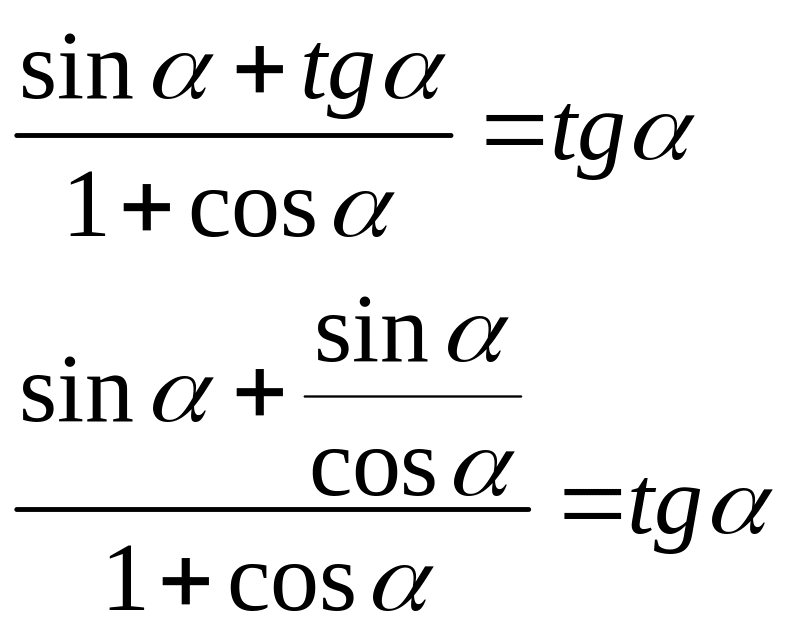
Приведем к общему знаменателю

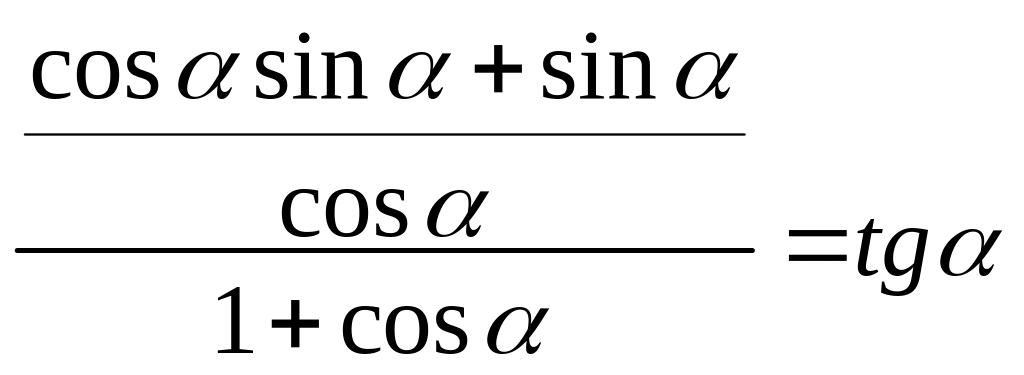
Вынося общий множитель и выполнив деление на , получим

Сократив на , получаем результат

В теме тригонометрические формулы сложения, т.е. для , а так же для формул двойного аргумента, т.е. для выполняются те же самые виды упражнений, что и для тригонометрических формул одного и того же аргумента. Способы решения в этих случаях ни чем не отличаются.

Например. Упростить выражение

Первый вариант решения.

Заменяем на , а

Получим

Второй вариант решения.

Используем равенства

1

Получили

Ответ 2cosa

Рекомендуемая литература:

1. Математика: учебник для ссузов, НВ Богомолов и др.-М.; Дрофа 2005г.

2. Алгебра и начала анализа: Дидактические материалы для 10-11 кл. - М,: Мнемозина 1998г.

3. Практические занятия по математике: учебное пособие для техникумов-М,:

Высшая школа 1979г.

4. Сборник задач по математике: учебное пособие для ссузов - М, Дрофа, 2006г
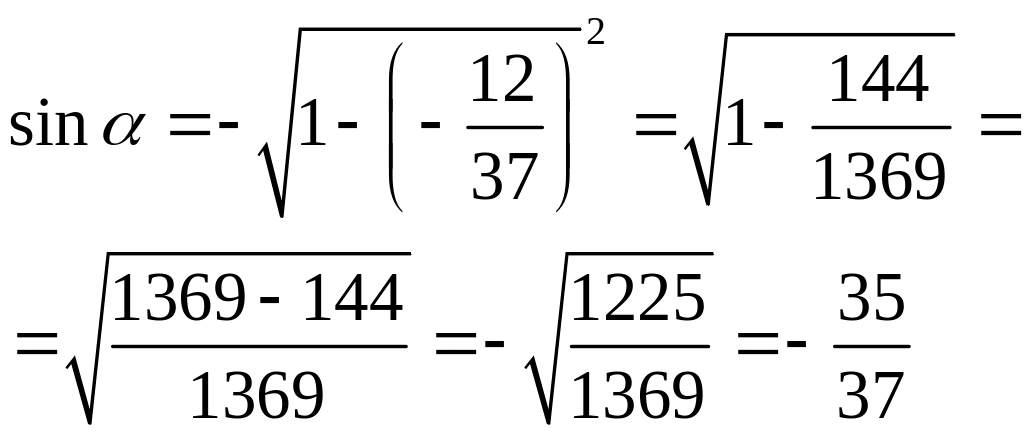
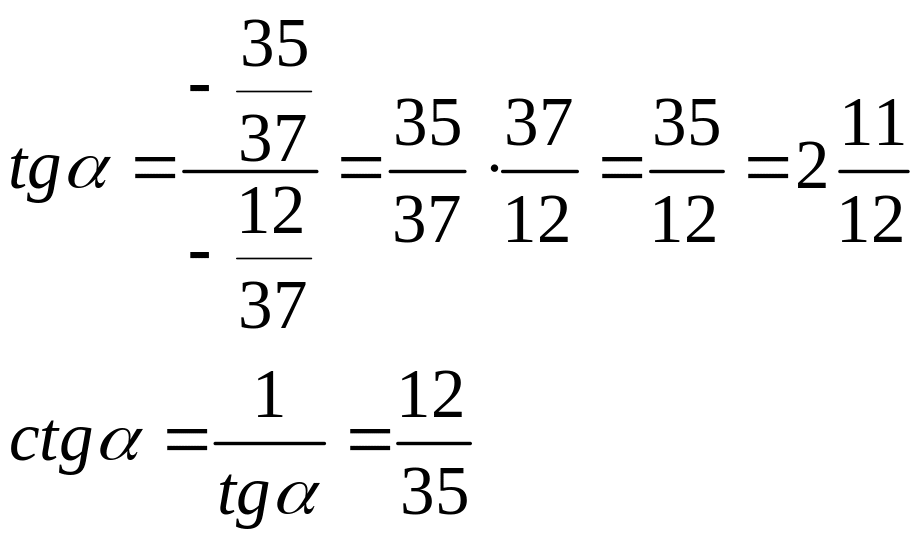