Тема. Понятие функции область определения и множество её значений. Чётность и нечётность функции, и её ограниченность.

Существует аналитический способ задания функции y-f(x), т.е. с помощью некоторой формулы. Формула f указывает на те действия, которые необходимо выполнить над аргументом x, ч то бы получить числовое значение функции.

С помощью формулы задающей функцию можем решать различные задачи.

Область определения функции y=f(x).

Пример 1.

Знаменатель не должен равняться 0.

Решение

Ответ:

Пример 2.

Т.к. х находится под корнем квадратным, то

Решение сводится к системе

Пример 3.

Решение

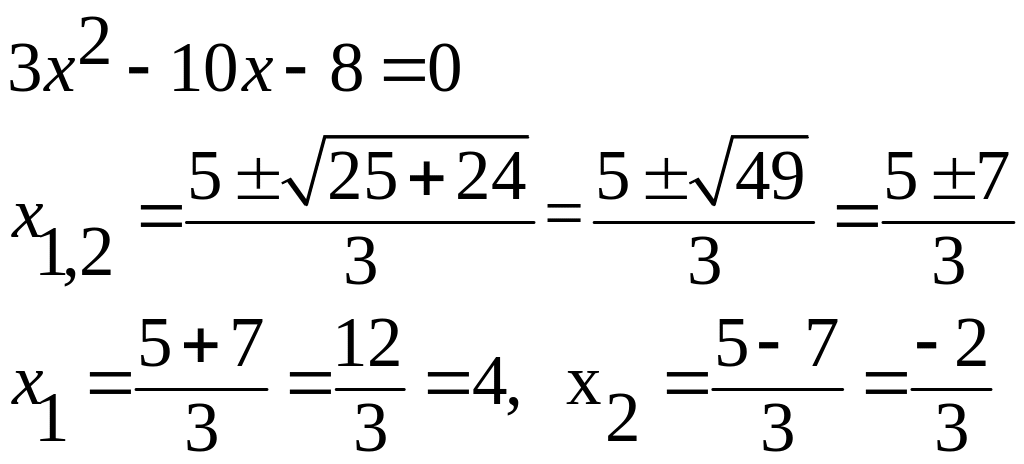
тогда область определения данной функции состоит из всех значений х, кроме чисел 4 и

Ответ:

Пример 4.

т.к. трёхчлен содержится под корнем квадратным, то

, а т.к. он же находится в знаменателе, то .

Решение

Область определения функции состоит из тех х, при которых

Решаем квадратное неравенство методом интервалов.

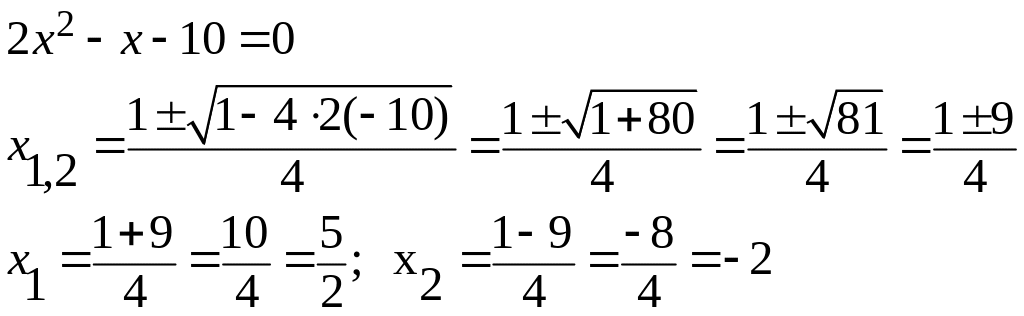
Получили интервалы на числовой оси, в которых определяем знаки квадратного трёхчлена .

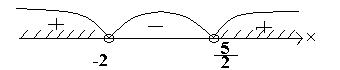
Т.к. , то заштриховываем интервалы, содержащие знаки +.

Ответ: х < -2; x > .

2. Чётные и нечётные функции.

Для решения вопроса о чётности и нечётности функции студенту необходимо знать определение чётной и нечётной функции и помнить что, sin(-x)=-sinx, tg (-x)=-tg(x), ctg(-x)=-ctgx (нечётные) и cos(-x)=-cosx (чётная).

Задание.

Исследовать функцию на чётность и нечётность.

Пример 1.

Решение: заменим х на – х в формуле

т.е. функция чётная на основе определения чётной функции.

Пример 2.

Заменим х на – х в формуле.

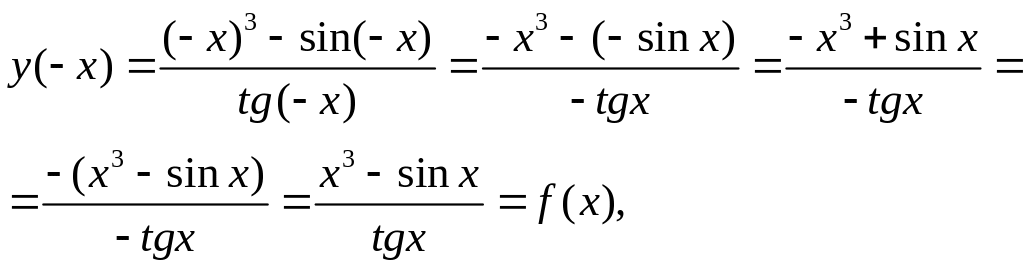
т.е. функция чётная по определению.

Пример 3.

Заменим х на – х в формуле.

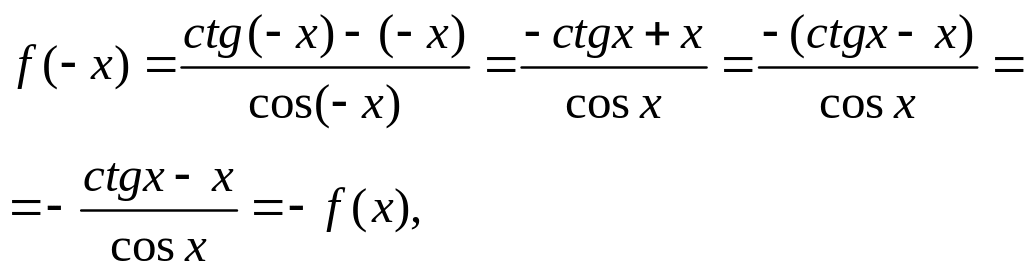
т.е. функция нечётная по определению нечётной функции.

Пример 4.

Заменим х на – х в формуле функции.

т.е. функция ни нечётная и ни нечётная;

В этом случае функцию называют функцией общего вида.

3. Множество значений данной функции удобнее всего определить по

графику её по оси ординат ОУ.

Задание.

Найти множество значений функции.

Пример 1.

y=-2x+3

Строим график функции по двум точкам из таблицы.

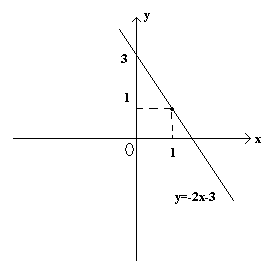
График показывает, что значение функции y=-2x+3 меняется от

Пример 2.

Т.к. в данной квадратичной функции а=-1, то ветви параболы направлены вниз, а это значит, что ордината вершины её будет наибольшим значением этой функции. Для решения задачи достаточно определить координаты вершины параболы и схематически построить график.

Решение.

- вершина параболы., а=-1, в=3, с=4

Строим график ветвями вниз.

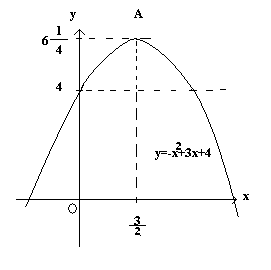
По оси ОУ видим, что все значения данной функции меньше числа .

Ответ:

4. Монотонность функции.

Возрастающие и убывающие функции в математике называются монотонными.

Графическое изображение позволяет найти интервалы монотонности.

Задание. Определить интервалы монотонности функции.

Пример 1.

y=3x-2

Решение

1. Строим график функции y=3x-2 по двум точкам.

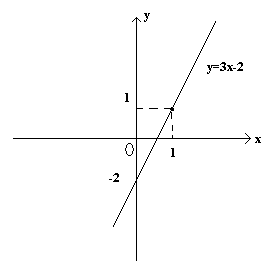
2. По графику видно, что с увеличением значений аргумента х по оси ОХ значения функции у так же возрастают по оси ОУ.

Ответ: у возрастает при .

Пример 2.

1. Строим график по характерным точкам.

а) -вершина

б) Точки пересечения параболы с ОХ при у=0.

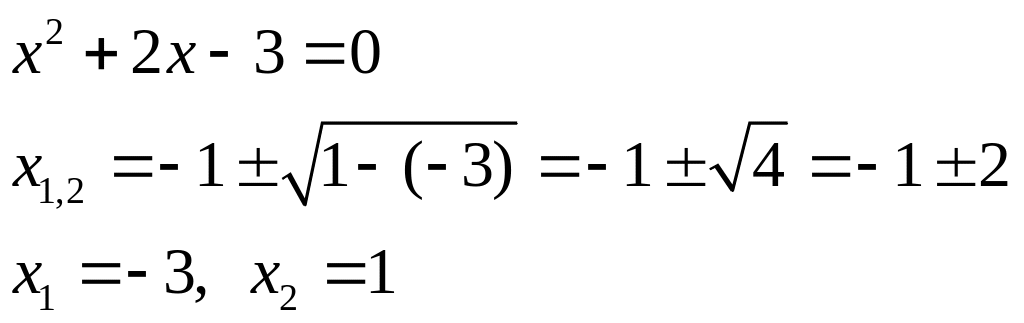
Точки пересечения с осью ОХ : (-3; 0) и (1;0)

в) Точки пересечения с осью ОУ при х=0

Точка будет (0; -3)

г) х=-1 – уравнение оси симметрии параболы.

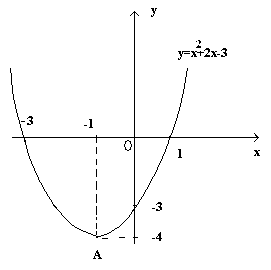
Из графика видно, что при всех х х<-1 левая ветвь параболы направлена вниз, что означает, что при х<-1 данная функция убывает.

Из графика наблюдаем, что при х>-1 левая ветвь параболы направлена вверх, что означает, что при х>-1 функция данная возрастает.

Ответ: при х<-1 функция убывает

при х>-1 функция возрастает.

5) Ограниченность функции.

Студенту необходимо знать, что ограниченными функции в элементарной математике являются y=sinx и y=cosx, т.к. известно, что

Для квадратичных функций вида (ветви параболы направлены вниз), значения функции ограничены сверху, а при a>0 (ветви параболы направлены вверх) значения этой функции ограниченны снизу.