Тема 9. Логарифмы. Логарифмические уравнения и неравенства.

Для освоения этой темы знание определения логарифма и свойств логарифмов обязательны.

Определение. Логарифмом числа а по основанию в называется такое число с, что выполняется равенство в^с=а и записывается в виде log_ba=c, где а>0, в>0, в≠1 и сєR логарифм.

Из определения получается основное тригонометрическое тождество

Свойства логарифмов при х>0, у>0, а>0, а≠1 и pєR:

1)log_а(xy) = log_аx+log_аy

2) log_аx/y= log_аx-log_аy

3) log_аx^p=p log_a^x

Эти свойства применяются в решении логарифмических уравнений, в вычислении значений логарифмических выражений.

Уравнение называется логарифмическим, если неизвестная величина содержится над знаком логарифма.

Виды логарифмических уравнений:

1) уравнения, решаемые на основе определения логарифма

2) уравнения, решаемые на основе свойств логарифмов

3) уравнения, сводящиеся к квадратным.

Логарифмические неравенства решаются на базе свойств монотонности логарифмической функции y=log_ax:

1) если а>1, то функция возрастает

2) если 0<а<1, то функция убывает

Если в логарифмическом неравенстве основание а>1, то при потенцировании знак неравенства не меняется.

Если в логарифмическом неравенстве основание 0<а<1, то при потенцировании знак неравенства меняется на противоположный.

Логарифмические неравенства в своем решении сводятся к решению системы неравенств, в которую включается и область определения данного неравенства.

Виды и способы решения логарифмических неравенств такие же как логарифмические уравнения.

Тема 10. Производная функция и ее применение.

Для усвоения темы необходимо научиться пользоваться определением производной функции y=f(x) в точке х₀, которое записывается в виде

=

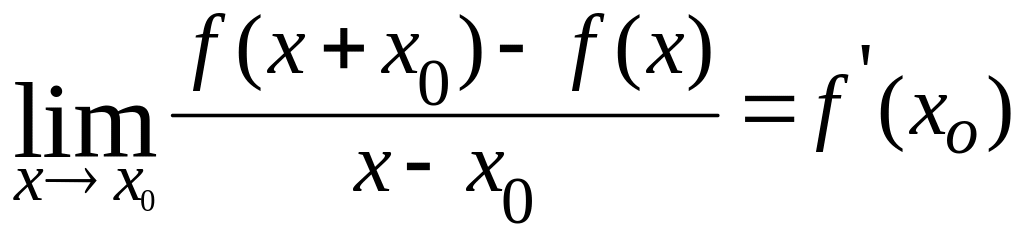
Из определения следует алгоритм вычисления производной:

1. f(x+∆x)

2. f(x+∆x)-f(x)

3.

4.

Производная имеет свой механический смысл, т.е. S'(t)=v(t) и V'(t)=a(t) и геометрический смысл, т.е. f'(x₀)=k, где k – угловой коэффициент касательной y=y₀+f'(x₀)(x-x₀) проведенной к графику функции y=f(x) в точке касания с абсциссой х₀.

Производная функции применяется в решении ряда физических задач и исследовании функции на монотонность, экстремумы ее, выпуклость и вогнутость графика.

Для решения этих вопросов используются специальные критерии.

Тема 11. Первообразная и интеграл.

Основой знаний этой темы является определение первообразной.

Определение: F(x) называется первообразной для f(x), если выполняется равенство F'(x)=f(x).

Свойство первообразной в том, что у функции f(x) первообразных бесчисленное множество, отличающихся друг от друга постоянной величиной, что символически записывается в виде F(x)+C, где С-const.

В математике выражение F(x)+C называется неопределенным интегралом от функции f(x) и обозначается символом ∫f(x)dx,т.е. ∫f(x)dx=F(x)+C.

f(x) – подынтегральная функция

f(x)dx – подынтегральное выражение.

Операция нахождения всех первообразных для данной функции f(x) называется интегрированием от латинского слова восстановление.

Для вычисления неопределенного интеграла пользуются свойствами:

1)постоянный множитель можно выносить за знак интеграла, т.е. ∫kf(x)dx=k∫f(x)dx

2)интеграл от алгебраической суммы функций равен алгебраической сумме интегралов этих функций, т.е. ∫(f₁(x)-f₂(x) + f(x))=∫f₁(x)dx-∫f₂(x)dx+∫f₃(x)dx

3) Существуют специальные приемы интегрирования. Это – 1)непосредственное интегрирование 2)метод замены в интегрировании.

Определенный интеграл имеет вид , где а нижний предел интегрирования и b – верхний предел интегрирования. Для вычисления такого интеграла существует формула Ньютона-Лейбница

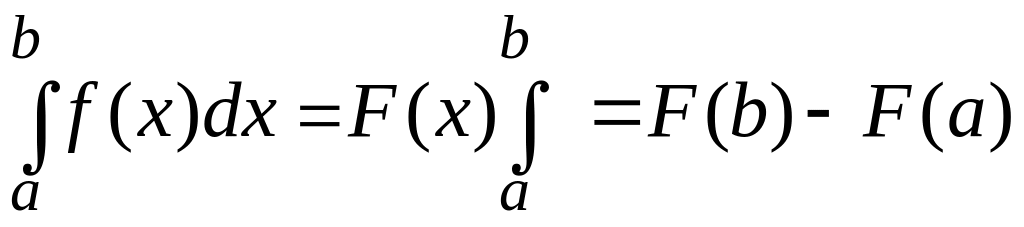
Свойства определенного интеграла те же, что и для неопределенного интеграла. Геометрически определенный интеграл означает величину площади фигуры, ограниченной линиями y=f(x), x=a, x=b и y=0.

Физическое приложение определенного интеграла в том ,что с его помощью можно вычисляется длина пути, пройденного точкой и величина произведенной работы под действием некоторой силы.