§9. Схема Бернулли

9.1 Основные определения и примеры

Введем следующую модель: пусть подбрасывается монета; при этом герб выпадает с вероятностьюp(назовем ее «вероятностьюуспеха»), а решка — соответственно с вероятностьюq= 1 − p(«вероятностьюнеудачи»).

Обозначим за P_n(m) вероятность того, что послеnбросков совершеноmуспешных (монета упала гербом). Этому соответствует набор элементарных событийA₁,A₂, …,A_n, где. Будем рассматривать события — двоичные последовательности вида, где 0 означает неудачу, а 1 — успех. Вероятность такой последовательности⁷равна. Проверим, что выбранная таким образом функция действительно задает распределение вероятности:

1. p(ω) > 0 —очевидно,

2. Докажем, что 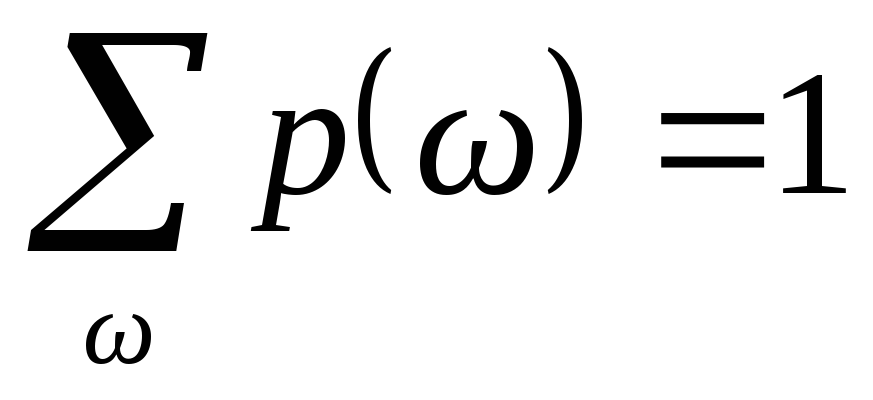. Запишем это выражение в виде

где L_m— число слагаемыхp(ω), для которыхmуспехов. Последовательностиωсостоят из нулей и единиц, имеют длинуn, иmединиц. Отсюда получаем. Тогда

.

Полученное нами при доказательстве выражение для вероятностиявляетсяосновнойформулой схемы Бернулли.

Функция распределения вероятности P_n(m) имеет максимум. Это видно из рассмотрения отношения

.

Действительно, P_n(m) возрастает при значениях этого отношения ≥ 1, и убывает в противном случае. Решим неравенство

.

Решение.

Получили: максимум будет наблюдаться приm= [p(n + 1)] =np.

График при p= 1/2 =q,n= 10,m= 0..10 приведен ниже:

Можно обобщить схему Бернулли на nопытов с вероятностямиp₁,p₂, …,p_kи определитьP_n(m₁,m₂, …,m_k) — вероятность того, что полученоm₁исходов первого типа, …m_kисходовk-го типа (m₁+m₂+ … +m_k=n). Оказывается, что при этом

.

При k= 2 очевидным образом получимP_n(m₁,m₂) =P_n(m,n−m) =P_n(m).

Примеры

1. Дана прямая, на которой выделены целые точки. Предположим, что некоторое существо (пьяное) выходит из нуля и каждую минуту с вероятностью pделает шаг вправо, а с вероятностьюq = 1 − p — влево.

Какова вероятность того, что через nсекунд оно вновь окажется в нуле?

Решение. Свяжем со случайными блужданиями схему Бернулли, обозначив шаг влево как неудачу, а шаг вправо — как успех. Если существо оказалось в нуле черезn= 2kшагов, то было сделаноm=kшагов вправо. Тогда вероятность, очевидно, равна. Например, приp = q = 1/2 получим.

2. На обобщение схемы Бернулли. Игральную кость бросают 5 раз. Найти вероятность выпадения 1 2 2 1 1 2(т.е., 1 раз выпала единица, 2 раза выпала двойка, …).

Решение.

.

3. Попробуем решить задачу 1) на плоскости. Пусть осуществляется случайное симметричноеблуждание (блуждание с вероятностью 1/4 пойти влево, вправо, вверх или вниз:p=q=r=s= 1/4).

В принципе, можно бы применить обобщение схемы Бернулли. Но эти средства сложны (требуется суммирование рядов и проч.), поэтому решать задачу мы будем исходя из других соображений. Заметим, что блуждания по xи поyне независимы (если частица сдвинулась влево на одном из шагов, она не сдвинулась ни вверх, ни вниз на этом шаге). Введем дополнительные оси координат, повернутые на уголπ/4:

Понятно: чтобы вернуться в исходную точку, необходимо вернуться по x′ и вернуться поy′. Запишем достаточно очевидные равенства для вероятностей:

P(x= 1) =P(x= 0) = 1/2

P(y = 1) = P(y = 0) = 1/2

P(x = 1, y = 1) = P(x = 1, y = 0) = P(x = 0, y = 1) = P(x = 0, y = 0) = 1/4

Обозначив , получим также

P(x′ = 1′) =P(x= 1,y= 0) +P(x= 0,y= 1) = 1/2,

аналогично

P(x′ = 0) =P(y′ = 1′) =P(y′ = 0) = ½

P(x′ = 1′,y′ = 1′) =P(x= 1,y= 1) = 1/4

и т.д.

Отсюда следует, что вероятность возвращения равна (поскольку события возвращения по x′ и вернуться поy′ независимы):

.

Заметим, что упростить задачу заменой координат в трехмерном случае не получится.

4. Задача о рассеянном курильщике. Рассеянный курильщик имеет 2 коробка спичек: в правом и в левом кармане пиджака. Изначально в них находится поnспичек. Вероятность выбрать коробок 1/2 на каждом «шаге». Каждый раз курильщик вынимает ровно по одной спичке. Найти вероятность того, что когда один коробок будет пуст, во втором окажетсяkспичек.

Решение. Будем рассматривать ситуацию, когда в правом коробке остается 0 спичек (рассмотрение противоположной ситуации аналогично; вероятности суммируются).

Самый сложный момент — сопоставление этой задаче схемы Бернулли. Объявим успехом событие «вытащена спичка из левого коробка», неудачу — «вытащена спичка из второго». Всего испытаний N= 2n−k. Из них успехов (n−k), неудач —n(правый коробок к концу испытаний пуст). Тогда

.

5. Проводятся n= 4 испытания по схеме Бернулли с вероятностью успехаp =1/4. Сравнить вероятности событийA: хотя бы один успех иB: ровно одна неудача.

Решение. Вероятность ровно одной неудачи — это вероятность ровно трех успехов:

.

Вероятность хотя бы одного успеха — вероятность дополнительного события к событию «все неудачи». Тогда

.

Вывод:P(A) > P(B).

6. Задача на независимость. Пусть дана электрическая цепь:

и вероятности выхода из строя ее отдельных компонентов:

P(K1)	P(K2)	P(λ1)	P(λ2)	P(λ3)
0,6	0,5	0,4	0,7	0,9

Найти вероятность того, что цепь разорвется.

Решение.Выделим блокK₃параллельно соединенных элементов. Согласно законам параллельного соединения, события выхода из строяλ₁,λ₂,λ₃независимы:

P(K₃) =P(λ₁)P(λ₂)P(λ₃) = 0,252.

С учетом этого упростим цепь до вида

Вероятность выхода из строя упрощенной цепи равна вероятности выхода из строя хотя бы одного ее элемента (событие А= {все работает}):

.