§7. Условная вероятность. Независимость

Условной вероятностьюсобытияAпри условии наступления событияBназывается величина

.

Легко видеть, что она удовлетворяет аксиомам вероятности (п. 6.2).

Замечание. Условная вероятность вводится из следующих соображений. Если приAпроизошлоB, естественно взять за вероятность такого событияP(AB). Однакопри таком условии будет равноP(B), а не 1; и аксиома 6.2.2 выполнена не будет. Произведя нормировку (поделив наP(B)), получим требуемое.

При решении задач определение условной вероятности записывают в виде

и называют теоремой умножения вероятностей.

События AиBназываютнезависимыми, когда

,

либо, что то же самое,

.

Эти два случая обычно не различают, и говорят, что AиBнезависимы, если вероятность их произведения равна произведению вероятностей:

.

Примеры

1. Дана колода из 36 карт. Вытаскивается одна карта. Определим события:

A — карта красная,B — карта — туз.

, т.е.AиBнезависимы.Однакостоит удалить одну карту из колоды, как независимость «исчезнет».

2. Р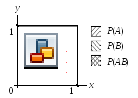ассмотрим единичный квадрат, все точки которого равновероятны (рис). Определим события:

.

Из рисунка видим, что

.

То есть, AиBнезависимы.Ноесли взять единичный круг, то независимости не будет.

События A, B, Cназываютсявзаимно независимыми(илинезависимыми в совокупности), если⁵

1. P(AB) = P(A) P(B),

2. P(BC) = P(B) P(C),

3. P(AC) = P(A) P(C),

4. P(ABC) = P(A) P(B) P(C).

Если условие 4) не выполняется, а 1–3 — выполняются, события называют попарно независимыми.

Из попарной независимости независимость в совокупности вовсе не вытекает.

Пример. Даны три попарно независимых события:A,B,C. Их вероятности по 1/2. Вероятность событияABCравна 1/10.

1. Независимы ли эти события в совокупности?

Ответ: нет, т.к.P(ABC) ≠P(A) P(B) P(C).

2. Найдите вероятность P(D) того, что произошло хотя бы одно из событий.

.

3. Найдите вероятность P(E) того, что произошло ровно одно событие.

.

§8. Формула полной вероятности. Формула Байеса

Н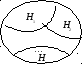абор событийH₁, H₂, …, H_nназываетсяполной группой событий(полным разбиением), если

1. ,

2. .

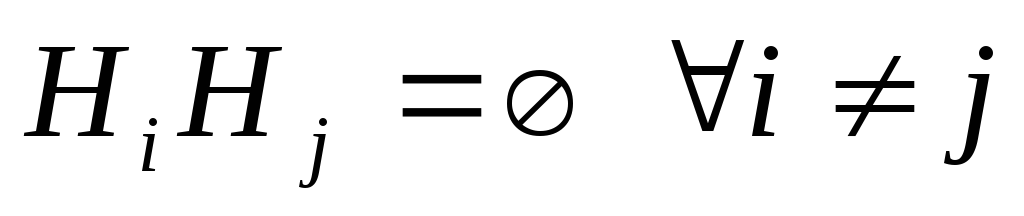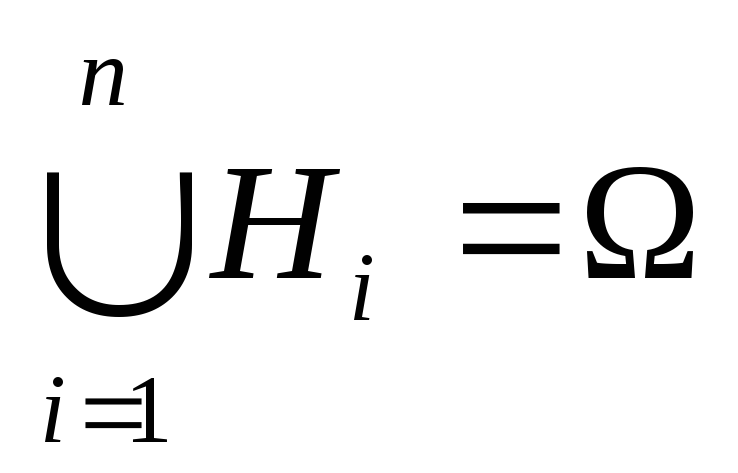Тогда выполняется формула

,

называемая формулой полной вероятности. ДалееH₁, …, H_nбудем называтьгипотезами. Если относительно некоторого событияAимеется полный набор гипотез, хотя бы одна из которых верна, мы можем разложитьAпо гипотезам с помощью этой формулы. Это более простой способ отыскания вероятностисобытия. Можно задаться вероятностямигипотез, и получитьформулу Байеса:

.

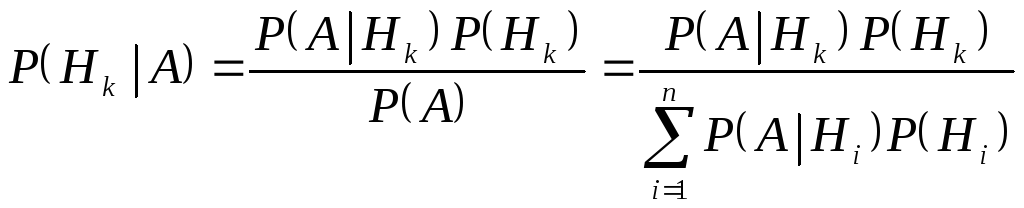Для чего это может понадобиться? Скажем, у нас есть некоторые гипотезы относительно события, для которых заданы вероятности. Мы производим опыт и узнаем его результат. С учетом наших новых знаний логично пересчитать вероятности гипотез, что и делают с использованием формулы Байеса.

Получить эти две формулы можно следующим образом.

1. Поскольку нам дана полная группа событий, мы можем «рассечь» событиеAна части, и записать

.

Тогда по аксиоме счетной аддитивности вероятности (п. 6.2.3)

.

2. Чтобы вывести ф. Байеса, применим известный метод «поделить и умножить на что-нибудь ненужное»:

.

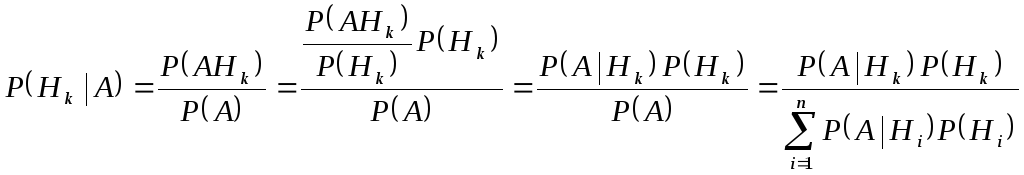Примеры

1. 3 завода выпускают телевизоры (продукция всех трех внешне выглядит совершенно одинаково). Первый завод выпускает 50% всей продукции, второй и третий — по 25%. На первом заводе 5% брака, на втором — 10, на третьем — 4. Какова вероятность того, что купленный телевизор — бракованный?

Решение. Введем гипотезы:H₁— телевизор изготовлен на первом заводе,H₂ — на втором,H₃— на третьем, и событиеA: телевизор бракованный. Тогда по формуле полной вероятности получим

.

2. Купленный телевизор — бракованный. Какова вероятность того, что он изготовлен на первом заводе?

Решение. Применим формулу Байеса:

.

3. В группе треть хороших студентов, остальные — средние. Хороший студент получает зачет с вероятностью 0,9, а средний — 0,5. Какова вероятность того, что случайно выбранный из группы студент получит зачет?

Решение. Обозначим заH₁: «студент хороший»,H₂— «студент средний»,A: студент получил зачет. Тогда

.

4. Изменим условие предыдущего примера. Пусть теперь можно получить зачет с одной либо с двух попыток. Какова тогда вероятность события A: случайно выбранный студент получил зачет?

Решение. Посчитаем вероятности гипотез:

.

Тогда

.

5. Известно, что в результате одной или нескольких попыток студент получил зачет. Какова вероятность события A: это средний студент?

Решение. По формуле Байеса

.

Замечание. Вообще говоря, для выполнения формулы полной вероятности достаточно частичного разбиенияH₁, H₂, …, H_nсо свойствами:

1. ,

2. .

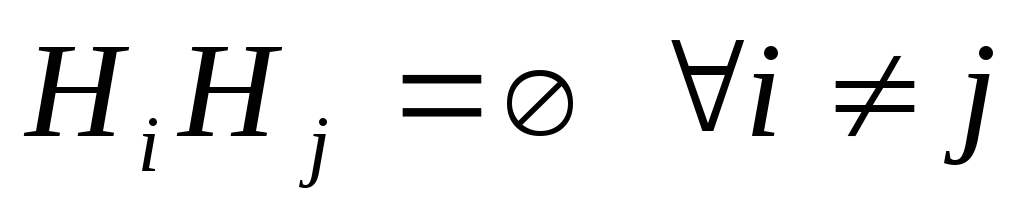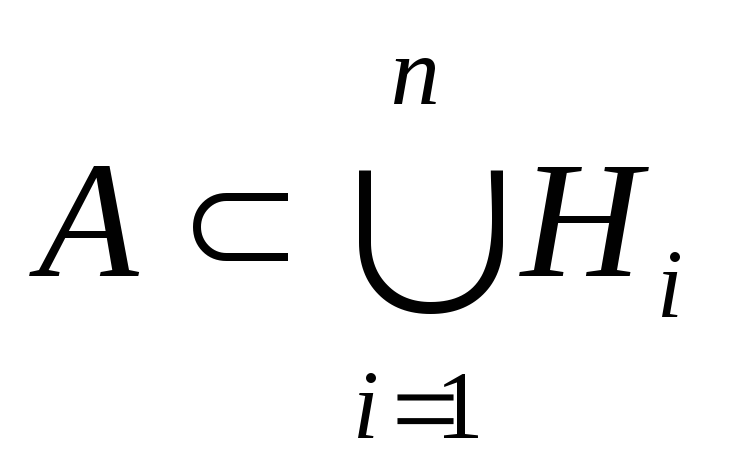Примеры

1. Студент ознакомился с половиной экзаменационных билетов. Если он знает билет, вероятность сдать экзамен равна 1/2, если не знает — 0. Найти вероятность успешной сдачи экзамена.

Решение. Возьмем в качестве гипотезH₁: студенту достался известный билет и H₂: достался неизвестный. Согласно условию задачи,P(H₁) =P(H₂) = 1/2; кроме того,P(A | H₁) = 1/2,P(A | H₂) = 0. Тогда вероятность событияA: экзамен сдан равна

.

2. Имеется полный набор костей домино (28 штук). Случайным образом выбираются 2 из них. Найти вероятность того, что одну кость можно пристаивть ко второй согласно правилам домино. Кости вытаскиваются последовательно (одна за другой).

Решение. Обозначим заH₁выпадение дубля (например, ), а за— выпадение любой другой кости (например, ). Тогда вероятность событияA: кость можно приставить равна

.

Действительно, есть 6 вариантов приложить кость к дублю, из 27 (одна кость взята). Дублей всего 7 (из 28). Аналогично с «недублями», прикладываемыми друг к другу — их 12 (из 27). Ну а P(H₂) = 1 − P(H₁).

3. Два разноцветных слона случайным образом ставятся на клетки шахматной доски. Найти вероятность того, что они бьют друг друга.

Решение. Легко проверить, что если первый слон стоит в левом верхнем углу, он бьет 7 клеток; то же самое — для всех четырех углов и вообще по периметру доски. Далее, слон, стоящий по периметру оставшейся части доски, бьет 9 клеток и т.д.:

7	7	7	7	7	7	7	7
7	9	9	9	9	9	9	7
7	9	11	11	11	11	9	7
7	9	11	13	13	11	9	7
7	9	11	13	13	11	9	7
7	9	11	11	11	11	9	7
7	9	9	9	9	9	9	7
7	7	7	7	7	7	7	7

С учетом этого введем гипотезы H_n: 1-й слон поставлен в клетку с числомn, гдеn{7, 9, 11, 13}. Тогда вероятностьAтого, что 2 слона бьют друг друга, будет равна

.

4. Пусть события A₁,A₂, …,A_nнезависимы в совокупности.P(A_i) = 1/3 (i = 1..n)

Введем событие A: произошло хотя бы одно изA₁,A₂, …,A_n. НайтиP(A).

Решение. Здесь проще рассчитать вероятность события: ни одно изA_iне произошло. Поскольку вероятности, аA_iнезависимы в совокупности, получим

.

Отсюда искомая вероятность равна

.

Заметим, что здесь мы воспользовались (интуитивно очевидным) фактом: если события независимы, то и их дополнения независимы.

5. Докажем факт, использованный при решении примера 4), для двух событий⁶. Пусть событияAиBнезависимы. Тогда их отрицания тоже независимы.

Доказательство. По определению независимости,

.

Преобразуем выражение, вспомнив, что :

.

6. Есть 30 шаров, пронумерованных от 1 до 30, и три урны, содержащие шары:

• первая — 1..9,

• вторая — 10..20,

• третья — 21..30.

Из случайно выбранной урны взяли один шар, и оказалось, что его номер делится на 5. Какова вероятность того, что шар взят из первой урны?

Решение. Естественно использовать формулу Байеса: вначале мы имеем гипотезыH_n(n= 1..3) о нахождении шара в урне с номеромn; затем происходит событиеA: номер вытащенного шара делится на 5, и мы уточняем с его учетом вероятностьH₁. Поскольку урны равновероятны,P(H_n) = 1/3. Вероятность вытащить шар из первой урныP(A | H₁) = 1/9, т.к. в ней 1 подходящий шар (№5); аналогичноP(A | H₂) = 3/11 (шары №№ 10, 15, 20);P(A | H₃) = 2/10 (шары №№25, 30). Тогда

;.