§25 Типичные задачи, 2

1. Теория: Доказать критерий возвратности для цепей Маркова.

Обозначим через f_nвероятность вернуться в состояниеiнаn-м шаге при условии, что на предыдущих шагах возврата не произошло:

.

Тогда для возвратного состояния iсправедливо

.

Введем u_n — вероятность находиться вi-м состоянии наn-м шаге:

.

Запишем производящие функции

.

Если , оба ряда сходятся, т.к.f_n,u_n≤ 1.

Заметим, что для возвратного состояния

Легко проверить следующий факт:

.

(он вытекает из формулы полной вероятности. Вероятность вернуться в i-е состояние наn-м шаге равна вероятности впервые вернуться (заnшагов), либо вернуться заn−1 шагов и один шаг находиться вi-м состоянии и т.д.)

Отсюда следует (по формуле умножения рядов), что

т.е..

Следовательно,

Теперь устремим z→ 1. Если цепь возвратна, тоF(z) → 1, аU(z) → ∞. Но приz→1U(z) имеет вид. И наоборот, если ряд изu_nрасходится, то знаменатель 1 –F(z) равен нулю, и цепь возвратна.

2. Теория: условное математическое ожидание и условное распределение одного подвектора нормального вектора относительно другого.

Дан вектор

,

где xиy— подвектора вектораz. Условное математическое ожидание одного подвектора относительно другого:

,

где Ey— матожиданиеy,Ex— матожиданиеx,R— блочная ковариационная матрица:

.

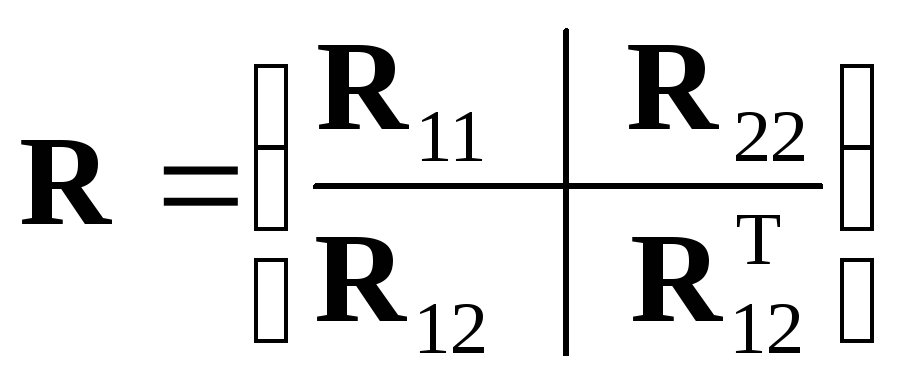Условное распределение

.

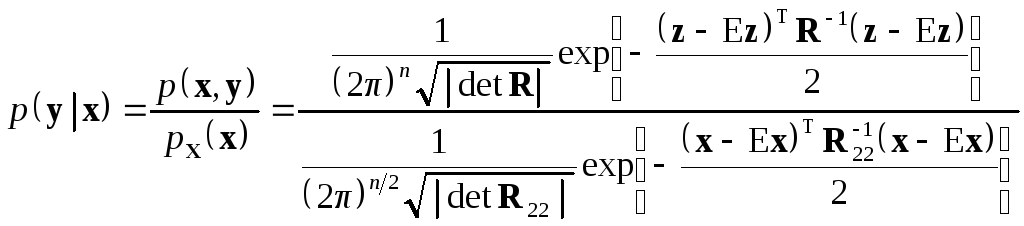3. Теория: многомерный нормальный вектор

По определению, если X₀— стандартный многомерный нормальный вектор, тоX=AX₀+b(вектор, полученный аффинным преобразованием¹²X₀).

,

где EX— вектор математических ожиданий,R— ковариационная матрица,n— размерность вектора.

4. Теория: свойства производящих функций

1) .

2) .

3)

5. Задача: даны 3 электрические цепи:

Вероятность выхода из строя каждого их приборов равна p= 0,1.

Найти вероятность того, что хотя бы одна из цепей проводит ток.

Решение.

.

6. Задача: игральная кость бросается до первого четного числа очков.X— количество бросков. Найти производящую функцию, математическое ожидание и дисперсию.

Решение. Производящая функция

Математическое ожидание:

Дисперсия:

7. Задача: при выстрелах по мишени вероятность попасть в «десятку» равна 0,1, в 9 — 0,3, в 8 — 0,5, в 7 — 0,05, в 6 — 0,05. Сделано 100 выстрелов. Какова вероятность того, что стрелок набрал не менее 820 очков?

Решение. Введем случайную величинуX_i — количество очков, набранных стрелком наi-м шаге. Ее ожидаемое значение

.

Найдем дисперсию:

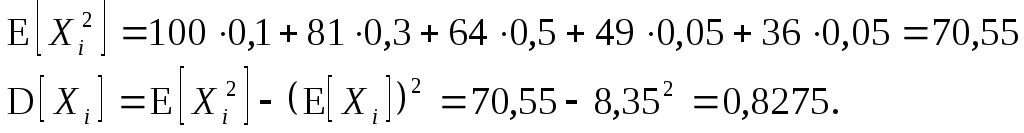
Суммарное количество очков равно

.

Искомая вероятность по ЦПТ

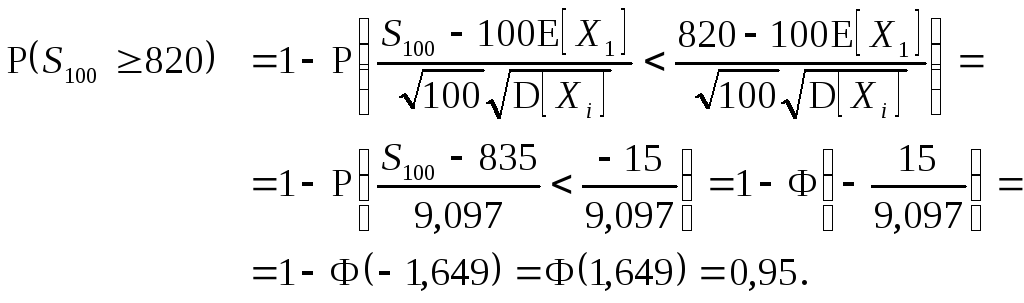
8. Задача: Корабельная пушка с равной вероятностью может выстрелить в любом направлении. Дальность полета не зависит от направления и распределена с плотностью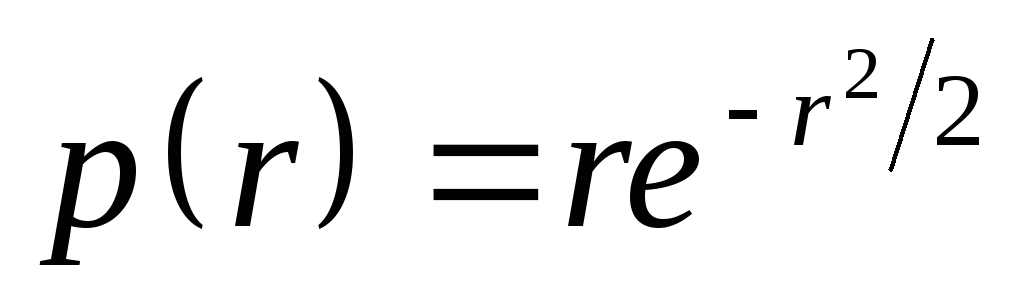. Найти двумерную плотность распределения координат (X,Y) падения снаряда.

Решение. Это задача на преобразование случайных векторов. Поскольку расстояниеrне зависит от углаφ, плотность совместного распределения равна

.

Выполним преобразование

,

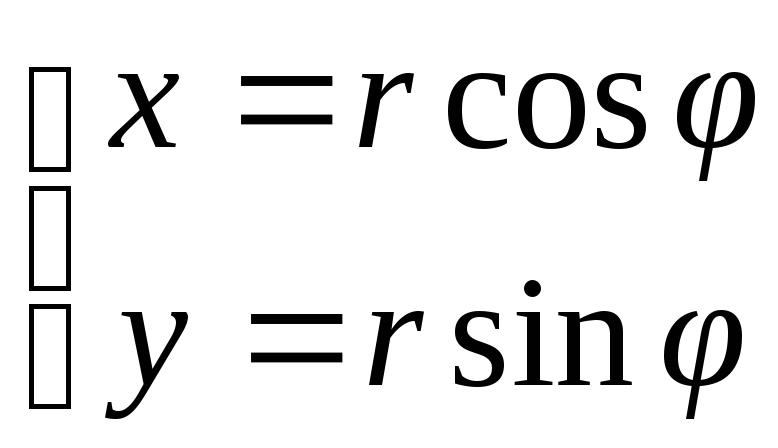его якобиан, как известно, равен r. Нам потребуется якобиан обратного преобразования — он равен 1/r. Получим для новой плотности распределения:

Таким образом, координаты независимы между собой, и каждая имеет стандартное нормальное распределение.

9. Задача: имеется Марковская цепь с матрицей

.

Найти предельное распределение перехода за nшагов (т.е., стационарное распределение).

Решение. Обозначим стационарное распределение за, тогда справедливо

,

где Oесть нулевая матрица. Упрощаем:

,

что равносильно системе уравнений

,

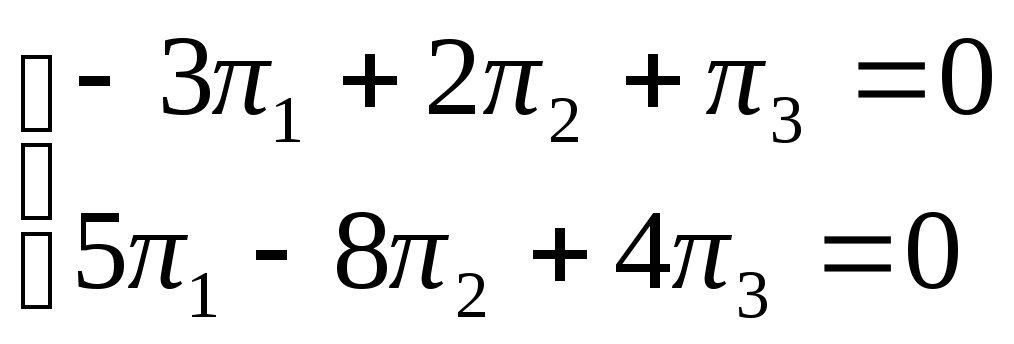откуда

.

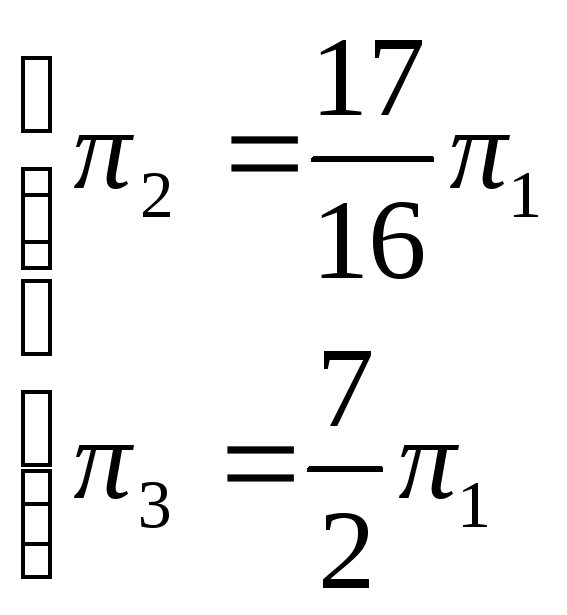Поскольку есть распределение, то, т.е.,

.

Окончательно получаем:

.

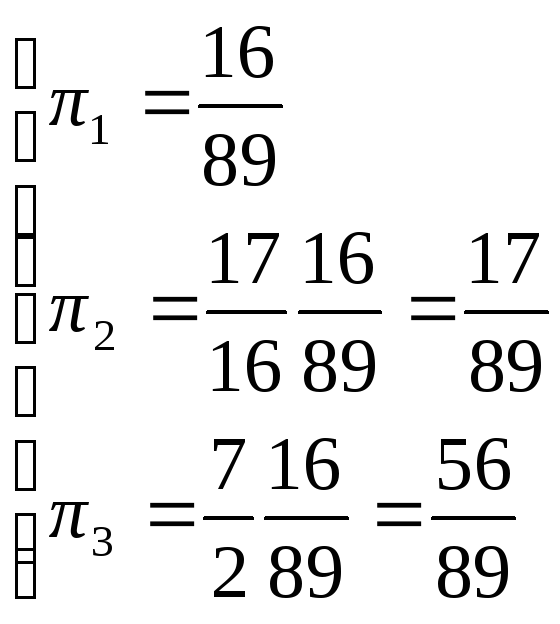1Т.е., вероятность каждого события равна 1/n.

2Из предыдущего §.

3То есть, операции над множествами.

4В том числе и конечное.

5Можно очевидным образом обобщить это определение наnсобытий. СобытияA₁,A₂, …,A_nназываются взаимно независимыми, если для любого множества индексоввыполняется равенство:

.

6Разумеется, справедливо и обобщение. Более того, одним из экзаменационных заданий является доказательство этого факта для большего числа событий.

7Мы используем дискретное определение вероятности.

8Применяется, когда вероятность успехаpвесьма мала (порядка 1/n), аλ< 10.

9Имеет стандартное нормальное распределение. Далее будем обозначать нормальное распределение с параметрамиaиσкакN(a,σ), а равномерное с параметрамиaиb— какU(a,b).

10Почему берется квадрат отклонения? Потому чтоE[X–EX] =EX–E[EX] =EX–EX= 0 («приращения и убыли значений случайной величины по сравнению с ожидаемым значением взаимно уничтожаются»). А модуль отклонения брать неудобно.

11Это условие излишне, так как следует из первого. Однако с таким допущением доказательство становится проще.

12Невырожденным.

81