
- •Глава 1. Теория вероятностей 3
- •1.2 Перестановки, размещения и сочетания
- •§2. Классическое определение вероятности
- •2.1 Определение и примеры
- •2.2 Критика классического определения
- •§3. Дискретное вероятностное пространство
- •§4. Геометрическая вероятность
- •§5. Парадоксы Бертрана
- •§6. Аксиоматика Колмогорова
- •6.1 Аксиомы событий
- •6.2 Аксиомы вероятности
- •6.3 Свойства вероятности
- •§7. Условная вероятность. Независимость
- •§8. Формула полной вероятности. Формула Байеса
- •§9. Схема Бернулли
- •9.1 Основные определения и примеры
- •9.2 Предельные теоремы в схеме Бернулли
- •§10. Случайные величины и их распределения
- •10.1 Введение
- •10.2 Функция распределения случайной величины
- •10.3 Наиболее употребительные распределения. Замена переменных
- •§11. Распределение случайного вектора (совместное распределение)
- •11.1 Основные определения
- •11.2 Плотность распределения случайного вектора при замене переменных
- •§12. Математическое ожидание случайной величины
- •12.1 Основные определения
- •12.2 Интеграл Лебега (интеграл по вероятностной мере)
- •12.3 Свойства математического ожидания
- •§13. Дисперсия случайной величины
- •§14. Примеры вычисления математического ожидания и дисперсии
- •§15. Производящие функции
- •15.1 Основные определения
- •15.2 Свойства
- •15.3 Примеры задач
- •§15. Коэффициент корреляции
- •§16. Многомерное нормальное распределение
- •16.1 Основные определения
- •16.2 Плотность распределения двумерного нормального вектора
- •16.3 Примеры задач
- •§17. Неравенство Чебышева
- •19.2 Закон больших чисел Бернулли
- •§20. Характеристические функции
- •20.1 Определение и свойства
- •20.2 Примеры
- •§21. Центральная предельная теорема
- •21.1 Доказательство цпт
- •21.2 Усиление закона больших чисел (збч Хинчина)
- •§22. Типичные задачи
- •§23. Условное математическое ожидание
- •23.1 Основные определения
- •23.2 Методы вычисления. Примеры
- •23.2.1 Дискретный случай
- •23.2.2 Непрерывный случай
- •23.3 Свойства
- •23.4 Исследование нормального случайного вектора
- •§24 Цепи Маркова
- •24.1 Основные определения. Формула Чепмена–Колмогорова
- •24.2 Классификация состояний
- •24.3 Период марковской цепи
- •24.4 Предельная теорема для переходных вероятностей марковских цепей
- •24.5 Возвратность цепей Маркова
- •§25 Типичные задачи, 2
§24 Цепи Маркова
24.1 Основные определения. Формула Чепмена–Колмогорова
Говорят, что последовательность случайных
величин
![]() обладаетМарковским свойством(являетсяцепью Маркова с дискретным
временем), если
обладаетМарковским свойством(являетсяцепью Маркова с дискретным
временем), если
![]() .
.
То есть, условное распределение последующего состояния цепи зависит только от текущего состояния и не зависит от всех предыдущих состояний.
Мы будем исследовать однородныецепи Маркова — такие, для которых условное распределение последующего состояния не зависит от момента времениn:
![]() .
.
При дальнейшем исследовании конкретные значения, принимаемые случайной величины, будут нам неинтересно; поэтому вместо них вводят состояния, нумеруемые целыми числами. Переход из одного состояния в другое (не обязательно от него отличающееся) происходит затакт(момент времени).
Тогда говорят о вероятности переходаиз состоянияiв состояниеj:
![]() .
.
Из {pij} очевидным образом можно составитьматрицу переходных вероятностей:
 .
.
Эта матрица обладает следующими свойствами:
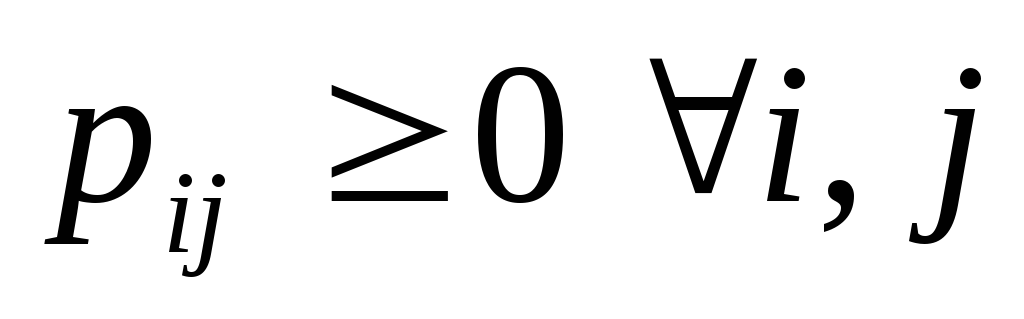 (вероятности — величины
неотрицательные),
(вероятности — величины
неотрицательные), (если мы вышли из состоянияi,
то обязательно за один такт перейдем
в некоторое состояниеj
).
(если мы вышли из состоянияi,
то обязательно за один такт перейдем
в некоторое состояниеj
).
Матрицы с такими свойствами называют стохастическими(случайными).
Матрице переходных вероятностей можно рассматривать как матрицу смежности некоторого взвешенного ориентированного графа — это повышает наглядность. Например, пусть
 .
.
Тогда соответствующий граф имеет вид

Уточним определение. Вообще говоря,
![]() .
.
Важной характеристикой цепи Маркова
является следующая: «При известном
настоящем прошлое и будущее независимы»
(то есть, цепь симметрично «повернута»
к прошлому и к будущему):
![]() .
Докажем это утверждение для частного
случая.
.
Докажем это утверждение для частного
случая.
![]()
Доказательство.

Введем матрицу переходных вероятностей за m шагов:

Как связаны между собой Pи![]() ?
Покажем, что
?
Покажем, что
![]() .
.
Действительно, пусть цепь вышла в некоторый момент времени из состоянияi. Введем гипотезуHk= {Xr=k} («в момент времениrцепь находится в состоянииk»). Тогда всевозможныеHkобразуют полную группу событий (поскольку в любой момент времени цепь находится в одном из возможных состояний). Значит, по ф. полной вероятности
![]()
Полученная нами формула носит название формулы Чепмена–Колмогорова. Ее можно записать в матричной форме:
![]() .
.
Отсюда следует тогда, что
![]() .
.
Таким образом, с вероятностной точки зрения цепь Маркова задается матрицей переходных вероятностей Pиначальным распределением
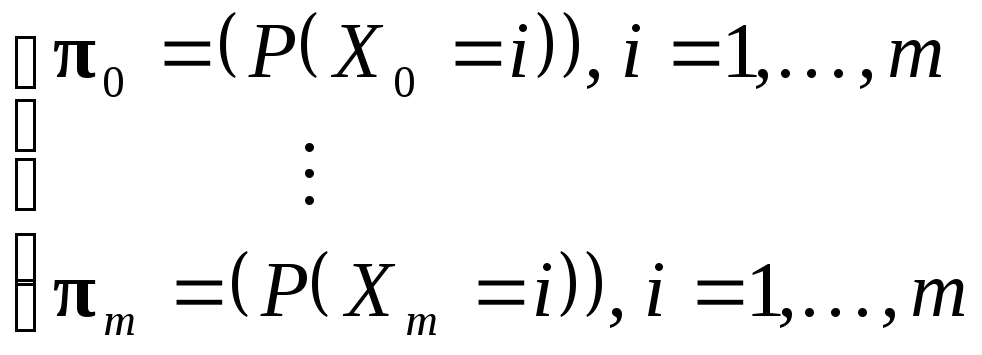 .
.
Из формулы полной вероятности видно, что
![]() ,
,
или, что то же самое,
![]() .
.
Это утверждение является формулой Чепмена–Колмогорова для распределения (а не для условного распределения).
24.2 Классификация состояний
Говорят, что состояние jдостижимоиз состоянияi,
и записываютi→j,
если![]() .
Если одновременно с этимj→i, состоянияiиjназываютсообщающимися,
и записываютi↔j.
.
Если одновременно с этимj→i, состоянияiиjназываютсообщающимися,
и записываютi↔j.
Если i↔j,j↔k, то иi↔k(то есть отношение ↔ транзитивно). Действительно, см. граф:

Возьмем некоторое состояние i1, и образуемклассI1состояний, сообщающихся с ним. Затем возьмем состояниеi2, и образуем классI2состояний, сообщающихся с ним и не входящих в классI1и т.д. Образованные таким образом классы {Ik} не пересекаются. В самом деле, пустьiI1I2. Тогдаi1↔i,i2↔i. По транзитивности получимi1↔i2, а, значит, по построениюi1иi2принадлежат одному классу состояний. То есть,I1=I2.
Кроме сообщающихся состояний в цепи могут существовать поглощающие(в них можно войти, но нельзя выйти), выделяемые в классI0, инесущественные(из них можно выйти, но нельзя войти), выделяемые в классI *.
Пример

В цепи, изображенной на рисунке, состояние 0 — несущественное, 1 — поглощающее, 2 и 3 — сообщающиеся состояния.
Обычно интересуются предельными свойствами цепей Маркова. Поэтому отбрасывают несущественные состояния (мы выходим из них за конечное число шагов) и поглощающие состояния (мы входим в них в конце и выйти уже не можем). Таким образом, изучаются лишь сообщающиеся состояния. Кроме того, в полученной цепи без несущественных и поглощающих состояний нет смысла рассматривать несколько классов сообщающихся состояний — они все «сливаются» в один.
