§23. Условное математическое ожидание

23.1 Основные определения

Вспомним определение условной вероятности:

.

Пусть дана случайная величина Xи событиеB, тогда

.

Теперь введем понятие условного математического ожидания:

1. — математическое ожиданиеXпри условии событияA.

2. — математическое ожиданиеXпри условии разбиенияH.

3. — математическое ожиданиеXпри условииσ-алгебры событийF.

4. — математическое ожиданиеXпри условии случайной величиныY.

Рассмотрим эти определения по порядку.

1. Полагают

,

при этом событие Aфиксировано.

2. Математическое ожидание при условии разбиения Hпространства событий Ω:

, если.

3. =, гдеHиFсвязаны между собой следующим образом: если естьH, то можно брать всевозможныеи их объединения, которые образуют некоторуюσ-алгебру. И наоборот, еслиF—σ-алгебра, мы можем указать разбиение, которому она соответствует.

4. Математическое ожидание Xпри условии случайной величиныY:

:Y —

в этом случае есть функция от случайной величиныY. Для конкретного значенияY=t:

.

23.2 Методы вычисления. Примеры

23.2.1 Дискретный случай

Пусть дискретная случайная величина X, зависящая отY, определяется таблицей

x y			
			
			
				
			

(, если.)

Тогда математическое ожидание Xпри условииY

Пример.Условное распределениезадано таблицей

x y	0	1
0	1/8	1/4
1	3/8	1/4

Найти .

Решение.

.

.

.

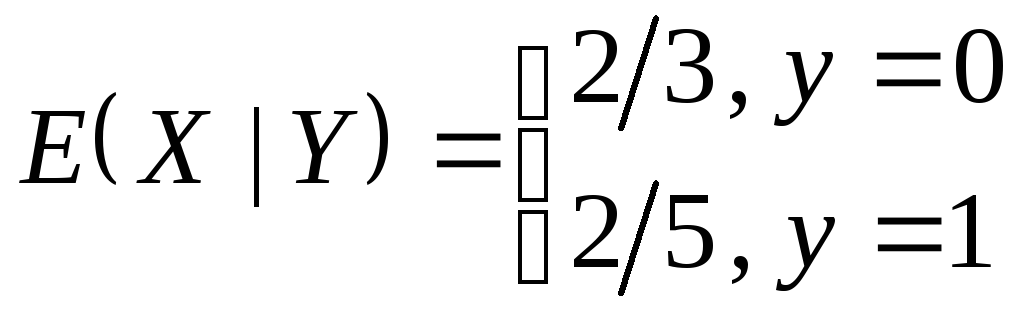23.2.2 Непрерывный случай

Пусть XиY имеют непрерывное совместное распределение с плотностьюp(x,y). Тогда

,

где – плотность распределенияY.

Или, что то же самое,

.

(при).

Пример

, в остальных точках.

Найти .

Решение.

23.3 Свойства

1. .

2. .

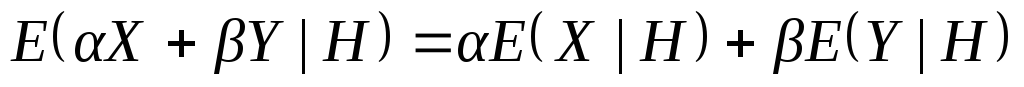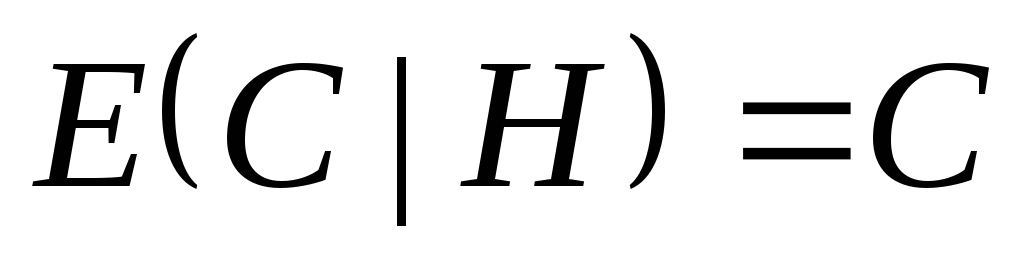3. Если , то

Дополнительное понятие. Пусть даны два разбиенияи. Будем говорить, что разбиениемельче, чем разбиениеи записывать это так, еслиможно представить как

,.

, потому что– постоянная на более крупном множестве.

Пусть всегда , тогда справедливо свойство

.

Доказательство:

.

В этом случае имеет роль константы и его можно выносить за знак математического ожидания.

4.

Доказательство:

1)

2) Рассмотрим дискретный случай. – случайная величина,.

Замечание. Несмотря на то, что мы рассмотрели лишьдискретныйслучай, все свойства условного математического ожидания справедливы и длянепрерывныхслучайных величин.

5. Если X,Y — независимые случайные величины, то

.

Доказательство:

.

6. .

Вытекаетиз доказанного свойства (самым грубым разбиением является разбиение на Ω и–, тогда возьмем разбиение именно таким).

Получим:

.

23.4 Исследование нормального случайного вектора

Пусть X₁— нормальный случайный вектор размерностиn, с математическим ожиданиемE[X₁] =cи ковариационной матрицейR=cov[X₁].

Пусть X₁разбит на два подвектора размерностейn₁иn₂,n₁+n₂=n:

,

аналогично разбит вектор математического ожидания:

.

Разобьем ковариационную матрицу на блоки:

,

где R₁₁=cov[x],R₂₂=cov[y],R₁₂— взаимная ковариационная матрица.

Решим промежуточную задачу: построим линейную комбинацию векторовXиYтакую, что она не зависит ни отX, ни отY. Воспользуемся тем, что равенство ковариации нулю и независимость компонент вектора равносильны. Требуется построить такую комбинациюX+BY, чтобыcov[X+BY,Y] = 0. (B— некоторая матрица). Распишем

Отсюда .Вывод: векторне зависит отY.

По одному из свойств условного математического ожидания это означает (при фиксированном подвекторе Y), что

то есть

Рассмотрим как частный случай две одномерные случайные величины, в двумерном случайном нормальном векторе (n₁=n₂= 1):

Условные математические ожидания:

В этом случае условное матожидание Xпри условииYназываютфункцией регрессии X на Y, матожиданиеYпри условииX— функцией регрессииYнаX.

Примеры

1. z = (x y)^T, Ez = (1 2)^T,

Найти .

Решение. Коэффициент корреляции

Соответственно,

2. Дан нормальный случайный вектор

Найти .Заметим,Y— число,x— вектор.

Решение. Так какxиYнекоррелированы,R₂₂=I,R₁₂= (1/2 …1/2). Тогда