§20. Характеристические функции

20.1 Определение и свойства

Характеристической функциейслучайной величиныXназывают преобразование Фурье распределения случайной величины:

.

Свойства

1. φ(0) = 1. (очевидно)

2. Если Y=aX+b, то.

Доказательство.

.

3. Важноесвойство. ПустьXиYнезависимы, тогда если , то.

Доказательство.

.

Естественно, это свойство распространяется и на бо́льшее число слагаемых:

.

4. φ(t) равномерно непрерывна.

Доказательство.

Полученное окончательное выражение зависит только от h. Для непрерывной случайной величины можно записать

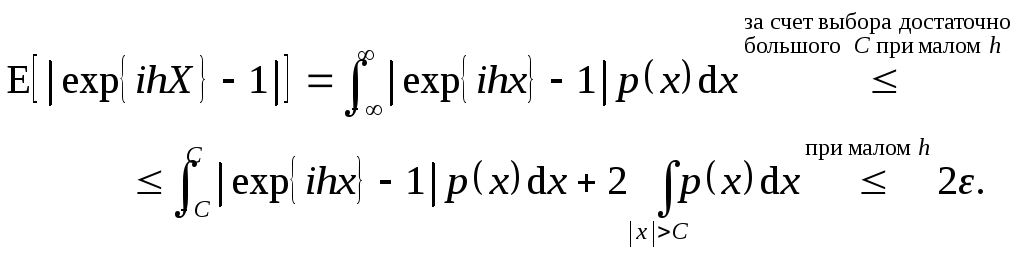
5. Пусть . Тогда

.

Доказательство. Если существуетk-й момент величиныX, то, пользуясь дифференцированием под знаком интеграла (что можно, посколькуp(x) существует), получим

.

При каждом последующем дифференцировании «сносится» i E[X], так что послеkдифференцирований получимi^kE[X^k]. Этот результат можно представить в виде

.

6. Характеристическая функция однозначно определяет распределение случайной величины.

Доказательство частных случаев

1. Пусть X — целочисленная дискретная случайная величина (k Z), тогда (обратное преобразование Фурье)

.

(ряд Фурье, коэффициентами которого являются p_k), тогда

.

Все слагаемые, при которых k≠m, дают 0 (по ортогональности), и остается

.

2. Пусть φ(t) абсолютно интегрируема на вещественной прямой, и существует плотность распределенияp(x)¹¹.

Попробуемвыразитьp(x) через характеристическую функцию. Запишем обратное преобразование Фурье функцииφ:

.

С учетом этого

Поскольку

в силу замены переменных получим

и, следовательно,

.

Если в (*) во втором интеграле оба предела интегрирования имеют одинкаовые знаки, получим 0; если разные — конечное число. То есть, ненулевой предел есть при a<y<b. В этом случае появится интеграл от −∞ до ∞, равныйπ. Отсюда

.

Получили:

,

следовательно, pполностью определяется характеристической функцией.

7. Важный факт(теорема о непрерывном соответствии): последовательностьтогда и только тогда, когда (альтернативно: в точках непрерывности распределенияF(x)).

8. Характеристическая функция всегда существует:

.

Доказательство..

9. Критерий характеристической функции

Функция φ_X(t) — характеристическая для случайной величиныXтогда и только тогда, когда:

1. φ_X(0) = 1,

2. φ_X(t) положительно определена.

Функция φ(t) называетсяположительно определенной(positivedefinite), если

причем равенство нулю достигается лишь при z_i= 0i. Если ослабить условие достижения равенства нулю, получимнеотрицательно определеннуюфункцию.

Проверим, что характеристическая функция положительно определена:

10. Разложение в ряд Тейлора: если , то

.

Обоснование. По свойству 5),

При k= 1, получаем,

При k= 2 —.

Если EX= 0,DX=E[X ²] = 1,.

20.2 Примеры

1. Проверить, является ли характеристической функцией, и если да, то какой случайной величины?

Решение. Приведем выражение к виду

.

Нетрудно видеть, что . После преобразования можно записать.

Рассмотрим значения p_i:

Вывод:cos²t — характеристическая функция дискретной случайной величины, принимающей значение 0 с вероятностью 1/2, а значения 2 и −2 — с вероятностью 1/4.

2. Вычислить характеристическую функцию вырожденнойслучайной величины:P(X= 0) = 1.

Решение..

Если же P(X=C) = 1, получим.

3. Проверить, является ли характеристической функцией, и если да, то какой случайной величины?

Решение. Приведем выражение к виду

.

Рассмотрим значения p_i:

Получили: это характеристическая функция дискретной случайной величины.

4. Пусть φ(t) — характеристическая функция случайной величиныX. Тогда— характеристическая функция какой случайной величины?

Решение. ПустьY=X–X′, тогда

Вывод: квадрат модуля любой характеристической функции — снова характеристическая функция.

5. Пусть X,Y — случайные величины с характеристическими функциямиφ_X(t) иφ_Y(t);a,b> 0 — константы такие, чтоa+b= 1. Рассмотрим функцию

.

Является ли она характеристической, и если да, то для какой случайной величины?

Ответ: да, является. Пусть соответствующие функции распределенияXиY — F_X(x) иF_Y(y). Рассмотрим функцию. Очевидно, это функция распределения, поскольку

.

Тогда плотность вероятности

.

Отсюда

6. Если φ(t) — характеристическая функцияX, тоφ(−t) — характеристическая функция (–X). (из примера 4)).

7. Пусть φ(t) — характеристическая функция величиныX, тогда является ли

f (t) =Re[φ(t)]

характеристической функцией некототорой случайной величины?

Решение. Очевидно,

.

Пусть φ(t) соответствует функции распределенияF_X(x), тогда дляRe[φ(t)]:

8. Пусть φ(t) — характеристическая функция величиныX, тогда является ли

f (t) =Im[φ(t)]

характеристической функцией некототорой случайной величины?

Решение. Нет, не является, посколькуf (0) = 0.

9. Найти характеристическую функцию нормального распределения.

   1. X ~ N(0, 1):

Сосчитаем φ(t), продифференцировав под знаком интеграла:

Решим дифференциальное уравнение с начальным условиемφ(0) = 1:

2. X~N(a,σ²): сопоставим такую величину сX₀~N(0, 1). Легко видеть, чтоX=a+σX₀. Тогда, по свойству 2)

.