§16. Многомерное нормальное распределение

16.1 Основные определения

Говорят, что случайная величина имеет нормальное распределение с математическим ожиданием aи дисперсиейσ², если ее плотность распределения

,

при a= 0,σ= 1 нормальное распределение называют стандартным.

Аналогичным образом определяют многомерную случайную величину с нормальным распределением: вектор X₀называютстандартным нормальным вектором, если все его компоненты независимы и каждая из компонент имеет стандартное нормальное распределение. Отсюда следует, что если мы рассмотрим совместную плотность распределения такого вектора, то

.

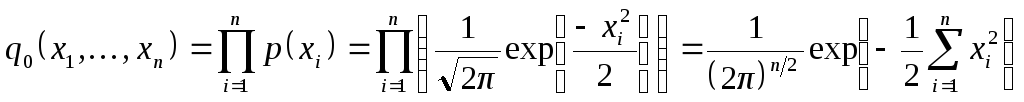В векторной записи

, (*)

где x^Tобозначает транспонирование вектораx.

Если вектор Yполучен линейным (вообще говоря, аффинным) преобразованием вектораX:Y=AX+b, гдеdetA≠ 0 (то есть, являетсяневырожденным нормальным вектором), согласно результату из п. 11.2 имеем

,

с учетом формулы (*) получим

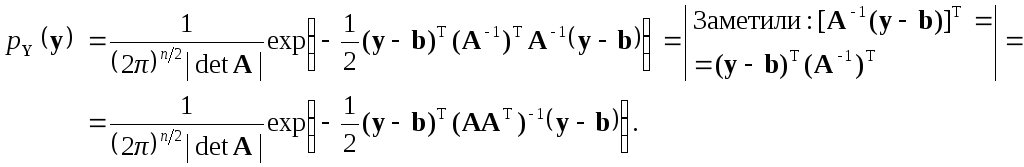
Оказывается, удобно описывать распределения в терминах матрицы Aлибо матрицыR=AA^T. Во втором случае запись плотности распределения становится компактнее:

.

Теорема. МатрицаRестьковариационная матрица вектораY:

.

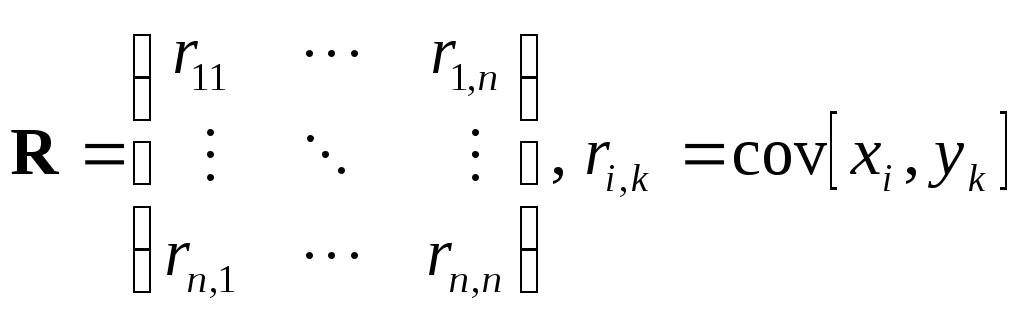В принципе, это следствие общей теоремы: если Y=AX(гдеX,Y— векторы,A— матрица линейного преобразования), тоcov[Y] =Acov[X]A^T. В Нашем случаеcov[X] =I(единичная матрица).Проверимэто утверждение непосредственно, для вектора размерности 2 (n= 2):

.

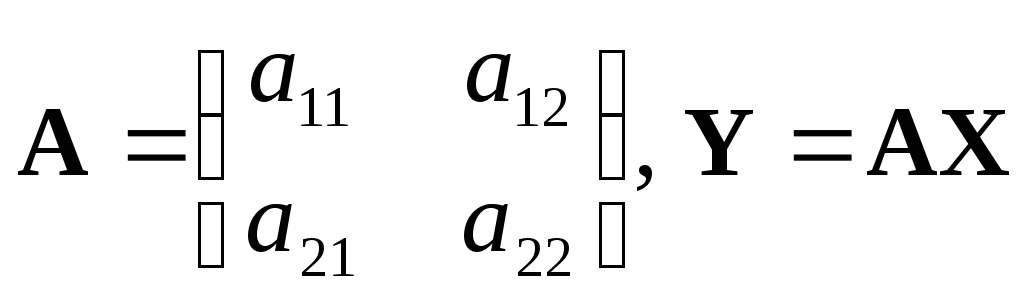Замечание. Вообще-то мы договорились ранее, чтоY=AX+b; однако векторbдает сдвиг, не влияющий на величину ковариации, поэтому не умаляя общности мы рассматриваем случайY=AX.

Распишем результат умножения AX:

.

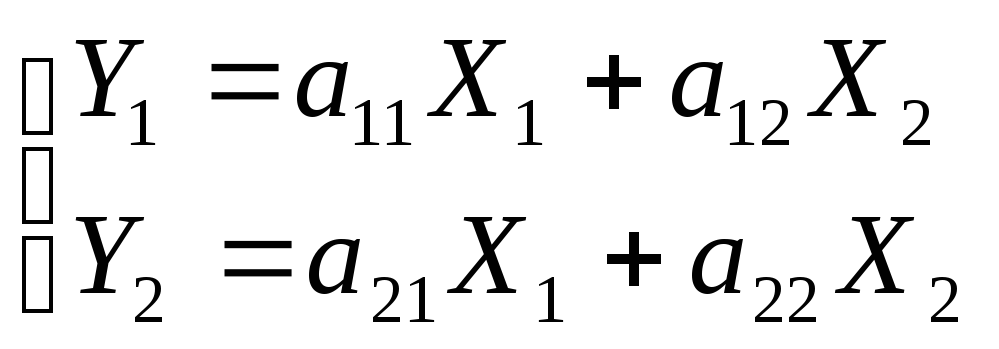Посчитаем ковариации (используя свойства стандартного нормального распределения):

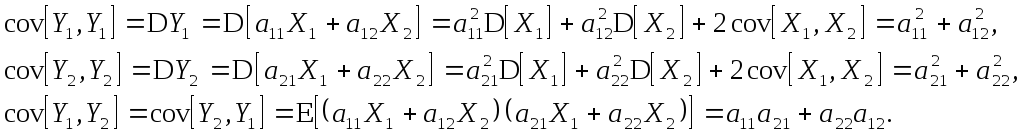
Тогда

.

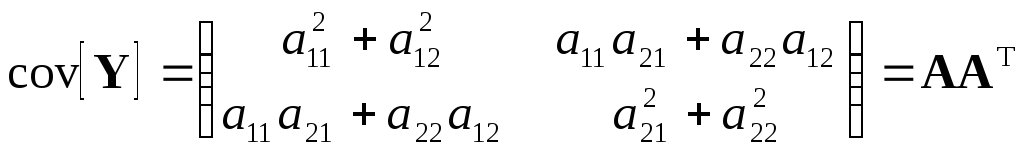Таким образом, выражение для плотности нормального вектора — выражение относительно матрицы ковариацииRи вектора математических ожиданийb. Действительно,Y=AX+b,EY=AE[X] +b=b;AA^T=R=cov[Y].

16.2 Плотность распределения двумерного нормального вектора

Как мы выяснили в предыдущем пункте,

,

где b = E[X], R = cov[X]. В скалярной форме приn= 2

,

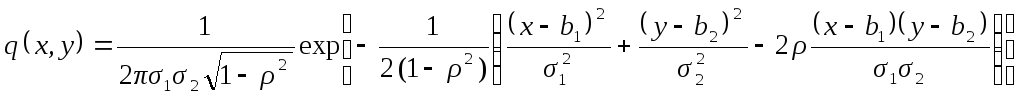где σ₁,σ₂— среднеквадратические отклонения (квадратные корни из дисперсий) компонентов вектора,ρ — коэффициент корреляции.

Свойства

1. Пусть X — нормальный невырожденный случайный вектор с математическим ожиданиемbи ковариациейR;Y=A₁X+с. ТогдаY— тоже невырожденный вектор, причемE[Y] =A₁b+c, а.

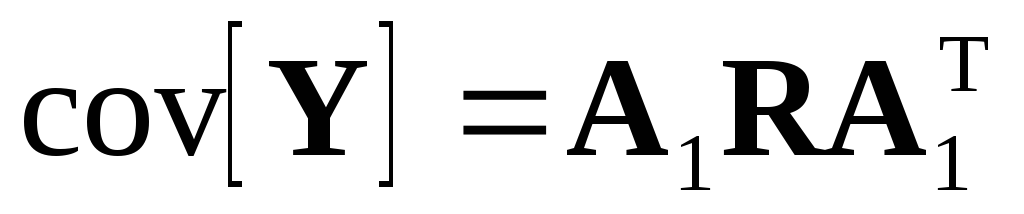Замечание. Согласно полученным формулам, распределение однозначно определяется его ковариационной матрицейRи вектором математических ожиданийb.

Доказательство. Случайный вектор. Рассмотрим

.

Получили: Y— тоже случайный вектор с нормальным распределением, у которого в качестве матрицыAвзята (A₁A), а в качестве матрицыb— (A₁b+c).

Заметим, что это справедливо и для вырожденного вектора (для которого).

2. Сумма независимых нормальных случайных величин имеет нормальное распределение.

Объяснение. Так как сумма является линейным преобразованием случайного вектора, справедливо свойство 1).

3. Если X — нормальные случайный вектор, а векторYимеет вид

Y= (a₁ X₁,a₂ X₂, …,a_n X_n)

(линейной комбинации коэффициентов вектора X), тоYимеет нормальное распределение.

Объяснение. Причина аналогична причине в п. 2).

4. Если X,Yсовместно нормальны, то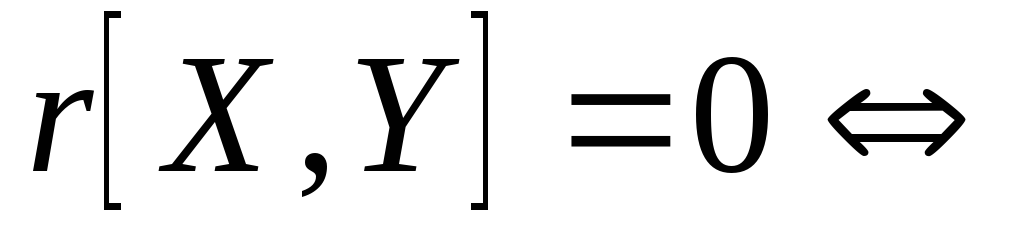X,Yнезависимы.

Доказательство. Это следует из формулы для плотности распределения приρ= 0:

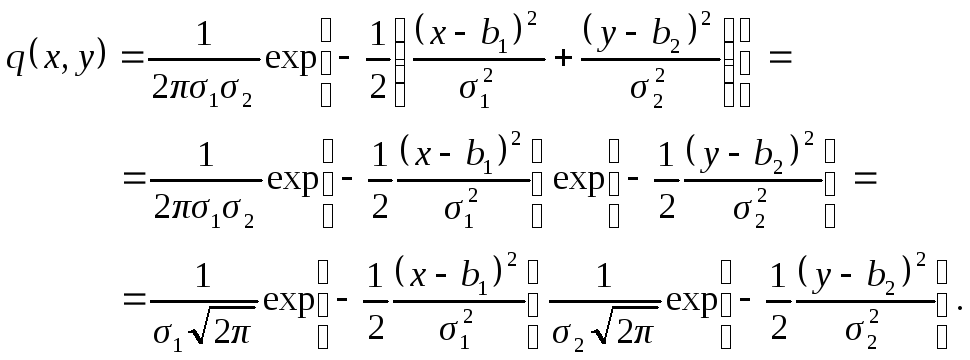
Получили: плотность распределения «распалась» в произведение плотностей нормальных распределений компонентов. Следовательно, X иY независимы.

5. Без доказательства. Если вектор нормален, каждый его подвектор также нормален.