§15. Производящие функции

15.1 Основные определения

Иногда для вычисления математических ожиданий степеней случайной величины X(центральных моментоввеличиныX) бывает удобно использоватьпроизводящие функции.

Пусть некоторая случайная величина Xпринимает лишь целые неотрицательные значения. Тогдапроизводящей функциейтакой величины называют функцию

.

Такая функция существует для всех , так как

.

На самом деле (доказывать мы этого не будем), Ψ(z) — аналитическая функция, и, стало быть, можно интегрировать и дифференцировать ряд почленно.

15.2 Свойства

1. Согласно формуле для коэффициентов степенного ряда,

.

Отсюда следует важный факт: производящая функция однозначно определяет случайную величину, т.к. все p_nопределены однозначно.

2. 

Доказательство. По правилу дифференцирования степенных рядов,

.

3. По правилу дифференцирования степенных рядов,

.

Отсюда легко видеть, что при z= 1

.

В частности,

Точно таким же способом можно находить произвольные моменты случайной величины.

4. При линейном преобразовании Y=aX+b:.

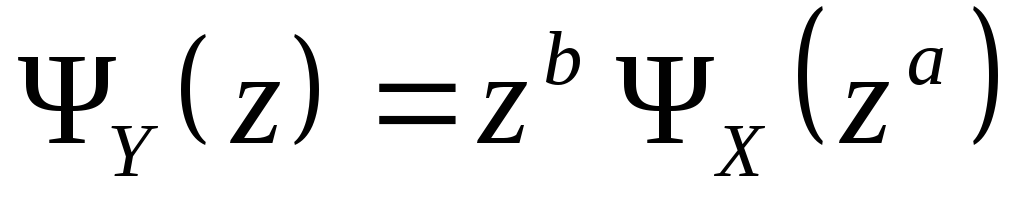Доказательство.

.

5. Если X,Y — независимые случайные величины, то.

Доказательство.

.

15.3 Примеры задач

1. Ψ(z) = 1/4 (1 +z)². Найти распределение случайной величиныX.

Решение.

2. Несимметричная монета бросается до первого выпадения орла. Вероятность выпадения орла P(X= 1) =p, решки —P(X= 0) =q= 1 –p.Y — число бросков. ВычислитьEY, DY, Ψ_Y.

Решение.

3. Случайная величина Xимеет распределение Пуассона с параметромλ:

Найти Ψ(z), первые три момента и доказать, что сумма независимых случайных величин с одинаковым распределением Пуассона также будет иметь распределение Пуассона.

Решение.

Теперь выполним доказательство. Рассмотрим производящую функцию для суммы 2 независимых случайных величин XиY:

.

Вывод: сумма тоже имеет распределение Пуассона, но с параметромλ. Заметим, что также нетрудно доказать (по индукции), что сумма изnслагаемых, имеющих одинаковое распределение Пуассона с параметромλ, имеет распределение Пуассона с параметромnλ.

§15. Коэффициент корреляции

Для двух случайных величин XиYвведемковариацию cov[X,Y] — меру зависимости между ними:

cov[X, Y] = E[(X − EX)(Y – EY)].

Свойства ковариации

1. Инвариантность к сдвигу:

cov[X − a, Y − b] = cov[X, Y], a, b = const.

Доказательство.

2. cov[aX, bY] = ab cov[X, Y].

Доказательство. Сначала упростим запись ковариации:

Полученное выражение несколько более понятно, чем определение ковариации. Действительно, если две случайные величины независимы, математическое ожидание их произведения равно произведению математических ожиданий (следовательно, ковариация равна нулю).

Теперь произведем замену /.{X→aX,Y→bY}, тогда

3. cov[X, Y] = E[XY] – E[X] E[Y]. См. доказательство в пункте 2).

4. Если X,Y— независимые случайные величины,cov[X,Y] = 0. С учетом 3)

Доказательство.cov[X,Y] =E[XY] –E[X] E[Y] =E[X] E[Y] –E[X] E[Y] = 0.

Внимание! Обратное неверно. Существуют зависимые случайные величины, для которыхcov[X,Y] = 0. Например, возьмем X ~ N(0,1), Y = X ². Тогда

Результат 0 получился из-за того, что под знаком интеграла стоит нечетная функция. Совершенно очевидно, что XиY— зависимые величины. Тем не менее их ковариация равна нулю.

5. Важное свойство:

.

Доказательство. По определению дисперсии,

.

Поскольку дисперсия не зависит от сдвига, будем считать E[X+Y] = 0. Тогда

Для решения многих задач удобнее использовать коэффициент корреляции— нормированную ковариацию:

.

Свойства корреляции

1. Инвариантность относительно сдвига:

r[X+a,Y+b] =r[X,Y].

Доказательство. Так как дисперсия и ковариация инвариантны относительно сдвига, то и корреляция инвариантна относительно сдвига.

2. r[aX, bY] = sgn[ab] · r[X, Y]

Доказательство.

3. Симметричность(очевидно):

r[X, Y] = r[Y, X]

4. −1 ≤ r[X,Y] ≤ 1, причем еслиabs[r[X,Y]] = 1, то междуXиYимеется линейная зависимость:Y=aX+b. Еслиr[X,Y] = 1,a> 0; еслиr[X,Y] = −1,a< 0.

Доказательство.

Пусть r = 1, тогда

Теперь пусть r = −1, тогда

Задачи

1. Случайный вектор (X,Y) равномерно распределен в круге (x − 1)² + (y − 2)²= 1. НайтиEX, EY, DX, r[X, Y].

Решение. Произведем замену переменных /.{X→X₁+ 1,Y→Y₁+ 2}:

Согласно произведенной замене, EX=EX₁+ 1,EY=EY₁+ 2;DX=DX₁,DY=DY₁. Отсюдаr[X,Y] =r[X₁,Y₁]. Плотность распределения

.

Пояснение. Простейшим примером совместного распределения двух случайных величин является двумерноеравномерное распределение на множестве A. Пусть задано ограниченное множествоAс площадьюσ. Оно определяется как распределение пары (X,Y), задаваемое с помощью следующей совместной плотности:

.

Математическое ожидание X₁

.

Аналогично, EY₁= 0. По формулам замены,EX= 1,EY= 2.

Ковариация

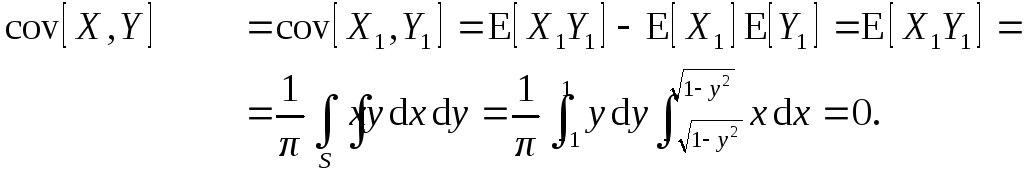
Дисперсия

2. Известно, что DX= 1,DY= 4,r[X,Y] = 1/2. Найтиr[2X+Y+ 1,X+ 2Y].

Решение. Так какcovнезависима от сдвига,

r[2X + Y + 1, X + 2Y] = r[2X + Y, X + 2Y].

Найдем ковариацию и дисперсии:

Тогда