§13. Дисперсия случайной величины

Дисперсиейслучайной величиныXназывается математическое ожидание квадрата отклонения этой величины от ее математического ожидания:

DX=E[X−EX]²

Интуитивно, дисперсия показывает «кучность» распределения X, т.е. близость конкретных значений случайной величины к ее математическому ожиданию¹⁰. Чем меньшеDX, тем более определено значениеX.

Свойства

1. DC = 0, при C = const (т.к. EC = C)

2. .

Доказательство. Действительно, изE[−EX+X]²= 0 с вероятностью 1 следует, чтоX – EX = 0 с вероятностью 1.

3. D[X + C] = D[X], при C = const. («инвариантность к сдвигу»)

Доказательство.D[X+C] =E[X+C–E[X+C]]²=E[X+C–EX–EC]²=

= E[X + C – EX – C]² = E[X – EX]² = DX.

4. D[CX] = C²DX, при C = const

Доказательство.D[CX] =E[CX–E[CX]]²=E[C²(X–EX)²] =

= C² E[X − EX]² = C² DX.

5. Если XиYнезависимы, тоD[X+Y] =DX+DY.

Доказательство. Будем рассматривать вместоX — (X–EX), вместоY — (Y –EY), при этом дисперсия, очевидно, не изменится (математическое ожидание есть константа). Тогда, не умаляя общности, будем считатьEX= =EY= 0, и

D[X+Y] =E[X+Y]²=E[X ²] +E[Y ²] + 2E[XY] =E[X ²] +E[Y ²] +

+ 2E[X] E[Y] = E[X ²] + E[Y ²] = DX + DY,

где E[XY] =E[X] E[Y] справедливо лишь в предположении о независимости величинXиY.

Заметим, что при тех же условияхD[X–Y] =D[X+Y] =DX+DY, поскольку константа (−1) в (X–Y) = (X+ (−1)Y) выносится в квадрате по свойству 4).

6. Часто оказывается полезной следующая формула вычисления дисперсии:

DX=E[X ²] – (EX)².

Доказательство.DX = E[X – EX]2 = E[X ²] – 2E[X EX] + E[(EX)²] =

= E[X ²] − 2(EX)² + (EX)² = E[X ²] – (EX)²_.

Вводят также стандартное отклонение(параметр масштаба). Откуда идет название «параметр масштаба»? А из свойства, гдеC=const— масштабный множитель (например, для перевода измеренной величины из одних единиц в другие).

§14. Примеры вычисления математического ожидания и дисперсии

14.1 Вырожденное распределение

X=const=C

EX=EC=C

DX=DC= 0

14.2 Распределение Бернулли

P(X= 0) =q,P(X= 1) =p,p+q= 1

EX=p· 1 +q· 0 =p

E[X ²] =p· 1²+q· 0²=p

DX=E[X ²] – (EX)²=p–p²=p(1 –p) =pq

14.3 Биномиальное распределение

Для отыскания математического ожидания

введем случайную величину

.

Заметим, что X= ∑X_i, аEX_i=pпо п. 14.2. Тогда

.

Так как производятся nнезависимыхиспытаний,X_iнезависимы между собой и дисперсия равна по п. 14.2

.

14.4 Распределение Пуассона

.

.

.

Вывод: параметрλв распределении Пуассона играет роль как дисперсии, так и математического ожидания.

14.5 Геометрическое распределение

Заготовки по суммированию рядов

Геометрическая прогрессия:

.

ПрирядAможно дифференцировать сколько угодно раз:

,.

Отсюда

.

При геометрическом распределении

Тогда

.

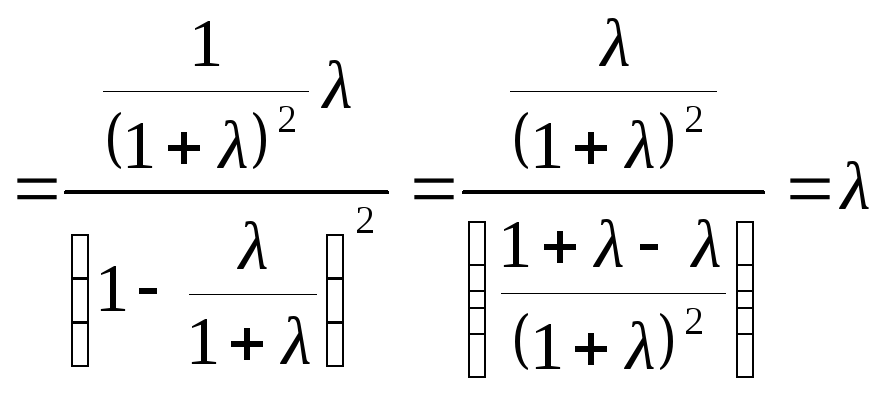Аналогично,

.

Отсюда

DX=E[X ²] – (EX)²= 2λ²+λ–λ²=λ²+λ.

14.6 Равномерное распределение на интервале [a,b]

.

.

.

При a= 0,b= 1 (стандартное равномерное распределение)EX= 1/2,DX= 1/12.

14.7 Показательное распределение

.

.

.

.

14.8 Симметричное показательное распределение

.

(т.к.p(x) четная).

.

14.9 Нормальное распределение

.

14.10 Другие задачи

1. Имеется дискретная случайная величина Xс распределением

x	0	π/6	π/2	5π/6	π
p	1/10	3/10	1/10	2/10	3/10

а случайная величина Y=sin X. НайтиEY,DY.

Решение. РаспределениеY имеет вид

y	0	1/2	1
p	2/5	1/2	1/10

Тогда

EY = 1/2 · 1/2 + 1 · 1/10 = 1/4 + 1/10 = 7/20,

E[Y ²] = 1/4 · 1/2 + 1 · 1/10 = 1/8 + 1/10 = 9/40,

DY = E[Y ²] – (EY)² = 9/40 – 49/400 = 41/400.

2. На гранях тетраэдра написаны числа 1, 2, 3, 4. Тетраэдр бросают на стол. Если он падает i-й гранью, то выигрыш составляет . Найти ожидаемое значение выигрыша и дисперсию, если совершено 10 бросков.

Решение. Введем случайную величинуX₁(выигрыш при одном броске). Тогда ее математическое ожидание равно

.

Матожидание квадрата X₁

.

Дисперсия

.

Тогда для 10 бросков выигрыш будет равен ожидаемый сумме матожиданий выигрышей при отдельных бросках:

EX= 10EX₁= 150/2 = 75.

Дисперсия при этом также увеличится в 10 раз:

DX = 10DX₁ = 1290/4 = 645/2.

3. Пусть X,Y ~U(0,1) и независимы,Z=max(X,Y). НайтиEZ, DZ.

Решение. Функция распределения

F(z) =P(Z<z) =P(X<z,Y<z) =P²(X<z) =z²,

плотность распределения p(z) = 2z(приz[0,1]). Тогда

4. Распределение случайной величины задано графиком:

.

Найти математическое ожидание и дисперсию.

Решение.

5. Пусть X,Y ~N(0,1) и независимы,U=max(X,Y),V=min(X,Y). НайтиE[U−V].

Решение.

P(U < x) = P(max(X, Y) < x) = P(X < x, Y < x) = P²(X < x) = Φ²(x).

Обозначим плотность распределения Uзаq, тогда

q(x) = (Φ²(x))′ = 2Φ(x) φ(x).

Математическое ожидание Uравно

Проводя аналогичные рассуждения для V, получим. Тогда.

6. Пусть X,Y ~N(0,1) и независимы, аY₁=exp{2X+ 3Y}. НайтиE[Y₁].

Решение. Можно было бы воспользоваться известным фактом, что линейное преобразование нормально распределенной случайной величины снова дает случайную величину с нормальным распределением. Однако в этой задаче проще поступить иначе. Т.к.XиYнезависимы, то

E[exp{2X + 3Y}] = E[exp 2X exp 3Y] = E[exp 2X] E[exp 3Y].

Теперь найдем

Последнее равенство верно в силу того, что под интегралом стоит плотность распределения N(a, 1). С учетом полученной нами формулы имеем

.