11.2 Плотность распределения случайного вектора при замене переменных

Пусть дан случайный вектор X,Y=φ(X) — вектор-функция:

,

и φудовлетворяет условиям:

1. Отображение φвзаимно-однозначно.

2. φдиффереренцируемо (требуется для замены).

3. Якобиан отображенияJ_φ(x) ≠ 0:

.

Тогда справедлива теорема:

.

(аналог одномерной теоремы о замене переменных).

Доказательство.

.

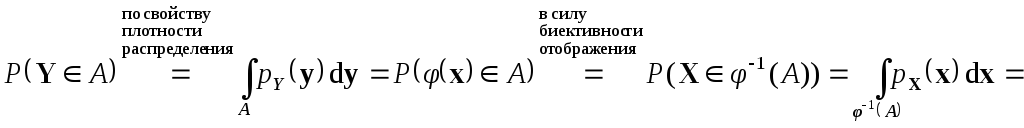
Сравним начальный и конечный интегралы и заметим, что равенство выполняется для любых n-мерных множествA. Отсюда

.

Примеры

1. y=Ax+b, гдеy,x,b— векторы,A— матрица линейного преобразования.

Тогда J_φ=detA,φ⁻¹(y) =A⁻¹(y−b),.

Если преобразование невырожденное, detA≠ 0 и справедлива формула

.

2. Говорят, что вектор X₀имеет стандартное нормальное распределение, если его компонентыx_i~N(0,1) и независимы между собой. Пустьn= 2. Требуется найти распределение (точнее, совместную плотность распределения) полярных координат вектораX₀= (x,y).

Переход к полярным координатам:

,

обратный переход:

дается соотношениями (из анализа):

.

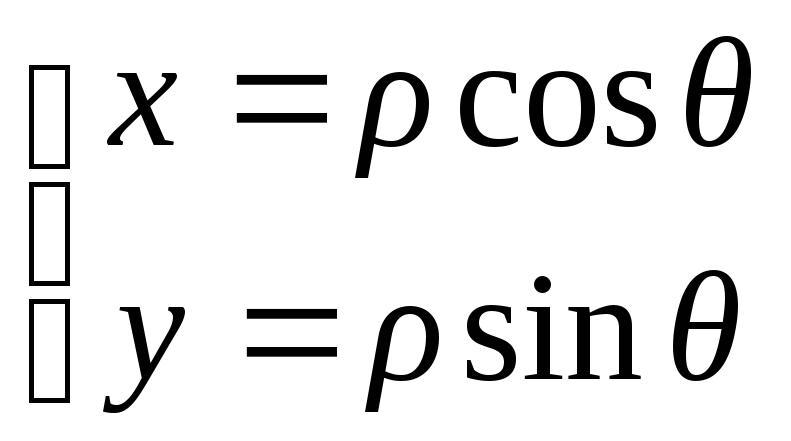Модуль якобиана отображения (опять же, из анализа) . Согласно теореме, плотность распределения

.

Поскольку координаты вектора независимы,

,

.

Отсюда

,

где —индикаторотрезка [0, 2π) (равен единице приθ [0, 2π), иначе нулю).

Получили: распределение полярных координат состоит из двух частей:— равномерное распределение углов,— распределение радиусов.

Замечание. Аналогичную задачу можно решить и для размерностиn= 3 (и, соответственно, сферических координат, модуль якобианаabsJ=ρ² cos θ). Но там потребуется расставить постоянные множители так, чтобы интеграл от плотности равнялся 1 дляρи дляθ.

§12. Математическое ожидание случайной величины

12.1 Основные определения

1) Пусть X — дискретная случайная величина, представленная конечными либо счетными наборами значенийx₁, …,x_n, … и вероятностейp₁, …,p_n, … Тогда

называется математическим ожиданиемслучайной величиныX.

Введем физическую интерпретациюматематического ожидания. Пусть на прямойXрасположены материальные точки с массамиp_i(для которых ∑p_i= 1) и координатамиx_i:

Тогда координаты центра масс определяются соотношением

.

Центр масс — характерная точка тела: тело движется так, как движется материальная точка с координатом в центре масс и массой ∑ p_i. Точно так же,EX — характерная точка (центр) распределения, показывающая поведение случайной величины в целом.

2) Пусть Xимеет непрерывное распределение с плотностьюp(x). Тогда

.

По аналогии с 1), можно ввести следующую интерпретацию: дана «материальная прямая», в каждой точке которой известна «масса» — вероятность

,

«центр масс» есть

.

12.2 Интеграл Лебега (интеграл по вероятностной мере)

Неформально. Рассмотрим ступенчатую функцию, равнуюx₁на Ω₁,x₂на Ω₂, …,x_nна Ω_n. Составим интегральную сумму, взявX_n=x_iприx_iΩ_i,i= 1, …,n.

С другой стороны, это математическое ожидание EX_n, т.к.. И можно сказать, что найдется такая возрастающая с вероятностью 1 последовательностьX_n↑X. Разумеется, при этомEX_n↑, и если его пределEXприn→ ∞ конечен, говорят, что функция (случайная величина)X(ω)интегрируема по вероятности:

.

12.3 Свойства математического ожидания

0. , гдеF(x) — функция распределения.Вывод: для вычисления математического ожидания случайной величины достаточно знать ее распределение. Эту запись следует понимать так: на вещественной прямой строится распределение вероятностей

Q([a, b)) = P(X  [a,b)) = F(b) – F(a),

и рассматриваются интегральные суммы

.

Для этого распределения вероятностей справедливы равенства:

• dF(x) = p(x) dx

• F(x) = F(x + 0)

• F(x) = P(X < x)

0. Лемма. Если задана функция от случайной величиныh(X), то

, еслиXдискретная,

, еслиXнепрерывная.

Если задана функция от случайного вектора h(X,Y), то

, если (X,Y) дискретный,

, если (X,Y) непрерывный.

Доказательство(для дискретного случая и одномерной случайной величины).

Y = h(X)

.

0. E(X+Y) =EX+EY(по свойствам интеграла)

Доказательство(для дискретной случайной величины).

.

Ясно, что это свойство распространяется на любое конечное число слагаемых.

0. E(CX) =C EX, еслиC=const(по свойствам интеграла)

1. (по свойствам интеграла)

2. (по свойствам интеграла)

3. Пусть X иYнезависимы, тогдаE[XY] =EXEY.

Доказательство. Воспользуемся леммой 1), взявh(X,Y) =XY. Тогда

.

0. EC = C, еслиC = const

1. E(X+C) =EX+C, еслиC=const(следует из 7) и 2)).